目录
题解的背景故事:其实这题题解早就发过了,但是wwj发现终于有人点赞了一年前的题解,却遭受了室友的嘲讽,"AI随便写"。wwj很不服,遂将题目给了小鲸鱼,结果被小鲸鱼薄纱。小鲸鱼使用了一种奇妙的矩阵做法,令刚在学OpenGL中复合变换的wwj很是兴奋,遂将此法写作题解。


一、题目描述

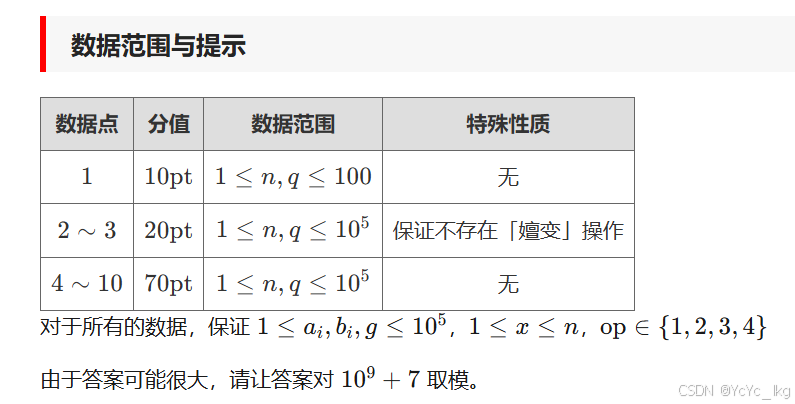
二、算法标签
数学,线性代数(矩阵乘法)
三、题解
这里建议先看原来的简单解法:LevOJ P2080 炼金铺 II-CSDN博客
首先将c[i]定为a[i]的初始值,d[i]定为b[i]的初始值,由于中间的操作无非就是+c[i],+d[i],+g,那么最终的答案肯定是ans=k1*c[i]+k2*d[i]+kc。由于中间我们只去记录操作,而不直接将操作结果作用在a,b上,所以ans=k1*a[i]+k2*b[i]+kc,那么问题就转化成了计算k1,k2,kc这三个系数的问题
我们定义一个三维矩阵,其第零行三个数分别表示k1,k2,kc,当进行+b[i]的操作时,就是把第一行的权值加到第零行上,当进行+g的操作时,就是把第二行的权值加到第零行上,那么当进行a[i]与b[i]的值互换的时候,就是交换了第零行和第一行(交换了操作关系)
所以我们的初始矩阵就是一个三维的单位矩阵,而最终矩阵的形式则是[k1,k2,kc],[0,k3,0],[0,0,1]
而中间将会经过一些列的矩阵变换,也就是说,我们需要提供三个变换矩阵,分别去对应炼金、嬗变、施法这三个操作。
①炼金:
首先我们知道,一个单位矩阵去乘以一个被操作矩阵,就是被操作矩阵原本的形式,而为了实现+b[i]的功能, 就需要去将被操作矩阵第一行的值累加到第零行上,这就需要将单位矩阵第零行第一列的值设置为1。最终的变换矩阵就是[1,1,0][0,1,0][0,0,1]
②嬗变:
嬗变操作将会交换a[i]和b[i]的值,也就是交换了矩阵的第零行和第一行,根据矩阵的计算法则,就需要将第零行第一列和第一行第零列置为1,同行的其他元素值为0。最终的操作矩阵就是[0,1,0][1,0,0][0,0,1]
③施法
该操作将会是单纯的累加,其实我们只需要每次将第零行第二列的值累加上g即可。不过为了统一变换,也可以设置一个操作矩阵[1,0,g][0,1,0][0,0,1]。
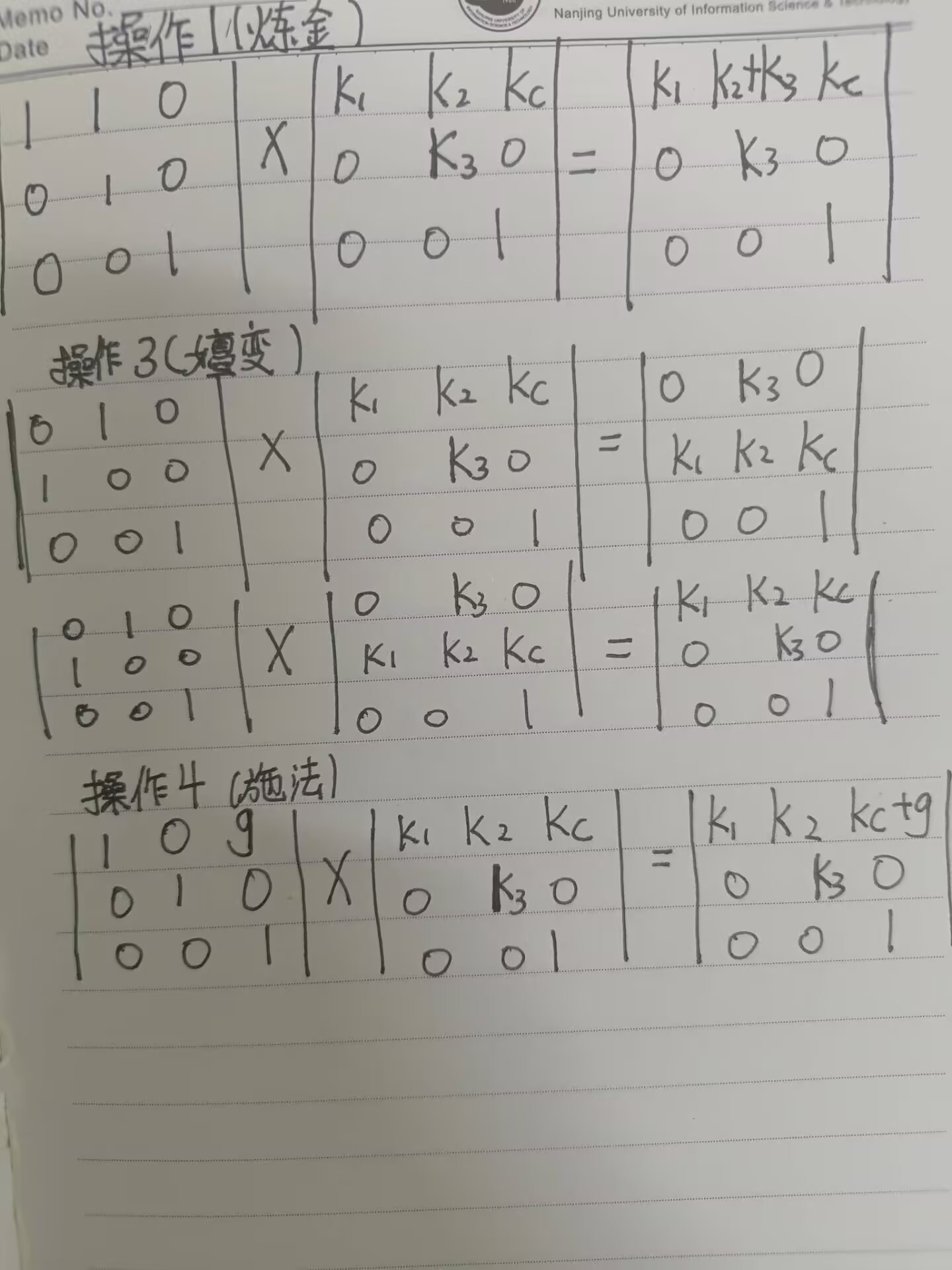
那么最终的结果实际上就是对于每次操作用相应的变换矩阵进行相乘即可,当执行检验操作的时候,就是取出矩阵第零行的系数,带入计算(别忘了取模就可以)。
代码:
cpp
#include<iostream>
using ll = long long;
using namespace std;
const int N = 1e5 + 5;
ll mod = 1e9 + 7, g, a[N], b[N];
int q, op, x, n;
struct Matrix
{
ll a[3][3];
Matrix()
{
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
a[i][j] = 0;
}
}
}
~Matrix() = default;
Matrix operator*(const Matrix& b)const
{
Matrix res;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
for (int k = 0; k < 3; k++) {
res.a[i][j] = (res.a[i][j] + a[i][k] * b.a[k][j]) % mod;
}
}
}
return res;
}
Matrix get_identity()
{
Matrix res;
for (int i = 0; i < 3; i++)
{
res.a[i][i] = 1;
}
return res;
}
};
Matrix transform, op_addb, op_swap, op_addg;
void pre_work()
{
transform = transform.get_identity();
op_addb = transform.get_identity();
op_swap = transform.get_identity();
op_addg = transform.get_identity();
//+b
op_addb.a[0][1] = 1;
//swap操作会交换第零行和第一行的值
op_swap.a[0][0] = 0;
op_swap.a[0][1] = 1;
op_swap.a[1][0] = 1;
op_swap.a[1][1] = 0;
}
int main()
{
std::ios::sync_with_stdio(false); cin.tie(0), cout.tie(0);
pre_work();
cin >> n;
for (int i = 1; i <= n; i++)cin >> a[i];
for (int i = 1; i <= n; i++)cin >> b[i];
cin >> q;
while (q--)
{
cin>>op;
if (op == 1)transform = op_addb * transform;
else if (op == 2)
{
ll res = 0;
cin >> x;
res = (transform.a[0][0] * a[x] % mod + transform.a[0][1] * b[x] % mod + transform.a[0][2]) % mod;
cout << res << '\n';
}
else if (op == 3)transform = op_swap * transform;
else
{
cin >> g;
op_addg.a[0][2] = g;
transform = op_addg * transform;
}
}
return 0;
}运行结果:
其实,毕竟需要进行矩阵的乘法运算,这个做法的运行效率并不优于先前的解法,但是,这种做法却会让人眼前一亮,而且在掌握的情况下完全可以跳过推导的过程直接使用,权当获得一种通法开拓思路吧!