一、算法比较
在准确性上,PELT算法通常优于二分分割法(BCD)等传统贪心算法。 因为PELT保证了全局最优解,而二分分割法只能得到一个近似的局部最优解。尤其是在变点较多、信号噪声较大或变点之间相互影响的复杂场景下,PELT的优势会更加明显。
然而,PELT的优势建立在正确设置惩罚参数的基础上。如果参数选择不当,也可能导致过拟合(变点过多)或欠拟合(遗漏变点)。在实际应用中,PELT因其在准确性和效率之间的出色平衡,已成为变点检测领域的主流和基准算法之一。
二、PELT算法
PELT算法的核心目标是在一个时间序列中,找到一组最优的变点(change points),将序列分割成若干段,使得段内数据的统计特性尽可能一致,而段与段之间的差异尽可能显著。它通过一个精巧的数学框架实现了这一目标,这个框架主要由四个部分组成:优化目标函数、惩罚参数、动态规划求解和剪枝策略。
首先,PELT将变点检测问题转化为一个数学上的优化问题。假设我们有一个时间序列
ELT的目标是最小化一个总的代价函数 J(τ),该函数由两部分组成:
拟合代价(Fitting Cost):衡量每个分段内数据与其统计模型的拟合程度。
模型复杂度惩罚(Penalty):惩罚过多的变点,防止过拟合。
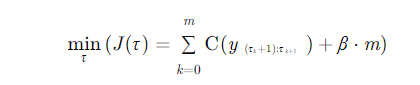
优化目标函数
公式中的C,将序列分割成若干段,将每段拟合一个数据模型,然后计算其代价。例如采用均值L2代价函数就是拟合水平线,代价是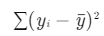
如果是斜率则不再是拟合一个水平线,而是拟合一条直线 y=ax+b。代价就是点到直线的距离。
这个函数是PELT灵活性的关键,可以根据检测目标的不同而选择不同的模型,例如均值、方差、AR、核方法(如RBF核),在趋势变化中我们一般选择线性的斜率 ,在波动率中可以选择方差。一般默认选择均值,实际上在趋势类中是不合适的,因为每个子段可能趋势相反但是均值相同。
惩罚参数
公式中的β。它被称为惩罚项(Penalty)或正则化系数。每多切一刀(多增加一个变点),总代价就要加上 β。注意β不是变点的数量,他是变点数量的系数,上面公式中的m才是变点数量。
β越大:算法越"保守",检测出的变点越少(宁可漏掉,绝不误报)。
β 越小:算法越"敏感",检测出的变点越多(宁可错杀,绝不放过)。
对于 PELT,通常使用 BIC 形式的惩罚,但是当数据噪声比较大的时候这种方法计算出的变点数量会相对实际变小,需要手动增大:
β=k⋅ln(n)
n:数据点的总数。
k:每个分段引入的参数个数(取决于你用的模型)。
线性模型(斜率+截距):每个分段增加 2 个参数,所以 k=2
动态规划 直接穷举所有可能的变点组合是不可行的(复杂度为 O(2的n次方)。PELT采用动态规划来高效地找到全局最优解。它的核心作用是量化一个时间序列分段(segment)内部的"不纯度"或"不一致性"。简单来说,它衡量的是如果我们将时间序列的某一段 [s,e]
视为一个独立的、统计特性稳定的区间,这个假设的"错误程度"或"代价"有多大。
剪枝策略剪枝的依据是代价函数的最优子结构性质和不等式关系。
三、算法实现
变点检测使用 ruptures 库实现,下面是一个检测斜率变化的案例。
参数:
min_size 最小的段含的点
model 用什么模型
penalty 惩罚系数
在algo = rpt.Pelt(model="linear", penalty="bic").fit(signal)加入参数,可以缺省,例如本案例中Pelt()缺失 min_size 。
import numpy as np
import ruptures as rpt
import matplotlib.pyplot as plt
# 1. 生成模拟数据:前50个点均值0,中间50个点均值10,后50个点均值0
n = 150
signal = np.concatenate([np.random.normal(0, 1, 50),
np.random.normal(10, 1, 50),
np.random.normal(0, 1, 50)])
# 2. 初始化 PELT 模型
# model="l2" 表示检测均值变化 (最常用)
# penalty="bic" 表示使用 BIC 准则自动计算 beta (也可以手动设 penalty=10)
algo = rpt.Pelt(model="linear", penalty="bic").fit(signal)
# 3. 预测变点
result = algo.predict() # 如果用了"bic",这里的pen会被忽略;也可以手动指定pen值,括号内写pen=10
# 4. 可视化
rpt.display(signal, result, figsize=(10, 6))
plt.title("PELT Change Point Detection (L2 Model)")
plt.show()
print(f"检测到的变点位置(索引): {result}")