LeetCode 1039.多边形三角剖分的最低得分：记忆化搜索（深度优先搜索）

【LetMeFly】1039.多边形三角剖分的最低得分：记忆化搜索（深度优先搜索）

力扣题目链接：https://leetcode.cn/problems/minimum-score-triangulation-of-polygon/

你有一个凸的 n 边形，其每个顶点都有一个整数值。给定一个整数数组 values ，其中 values[i] 是第 i 个顶点的值（即 顺时针顺序 ）。

假设将多边形剖分为 n - 2 个三角形。对于每个三角形，该三角形的值是顶点标记的乘积，三角剖分的分数是进行三角剖分后所有 n - 2 个三角形的值之和。

返回 多边形进行三角剖分后可以得到的最低分 。

示例 1：

复制代码

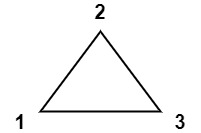
输入：values = [1,2,3]
输出：6
解释：多边形已经三角化，唯一三角形的分数为 6。

示例 2：

复制代码

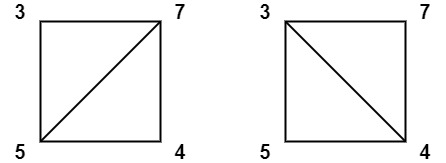
输入：values = [3,7,4,5]
输出：144
解释：有两种三角剖分，可能得分分别为：3*7*5 + 4*5*7 = 245，或 3*4*5 + 3*4*7 = 144。最低分数为 144。

示例 3：

复制代码

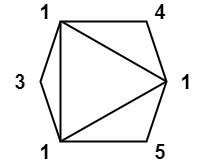
输入：values = [1,3,1,4,1,5]
输出：13
解释：最低分数三角剖分的得分情况为 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13。

提示：

n == values.length
3 <= n <= 50
1 <= values[i] <= 100

解题方法：DFS

借一张@灵茶山艾府的图：

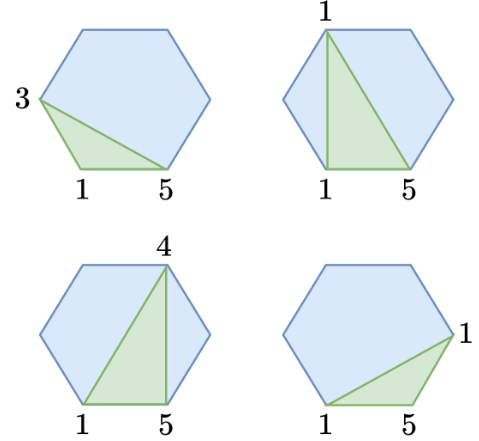
以边1-5为例，这条边最终一定在一个三角形中。在哪个三角形中呢？一共有图中这四种可能。我们分别枚举这4种可能就好了。

具体来说，我们可以写一个函数dfs(i, j)，代表从i到j的凸多边形的最低得分，那么将点k作为边15所在三角形的另一个顶点的话，得到的总得分为dfs(i, k)+dfs(k, j) + i*j*k。

时间复杂度 O ( n 3 ) O(n^3) O(n3)
空间复杂度 O ( n 2 ) O(n^2) O(n2)

AC代码

C++

cpp 复制代码

/*
 * @Author: LetMeFly
 * @Date: 2025-09-29 18:44:48
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2025-10-01 20:38:27
 */
#if defined(_WIN32) || defined(__APPLE__)
#include "_[1,2]toVector.h"
#endif

class Solution {
private:
    unordered_map<int, int> cache;
    vector<int> values;
    int n;

    int dfs(int i, int j) {
        if (j - i < 2) {
            return 0;
        }
        int key = i * n + j;
        if (cache.count(key)) {
            return cache[key];
        }
        if (j - i == 2) {
            return cache[key] = values[i] * values[i + 1] * values[i + 2];
        }
        int ans = 1000000000;
        /*
        0 1 2 3 -> 0 1 2 + 0 2 3

        0   1

        3   2


        0 1 2 3 4


            3
                 
        4        2

         0      1

        
        (i,j,k) + dfs(i,k)+dfs(k,j)
        */
        for (int k = i + 1; k < j; k++) {
            ans = min(ans, dfs(i, k) + dfs(k, j) + values[i] * values[k] * values[j]);
        }
        return cache[key] = ans;
    }
public:
    int minScoreTriangulation(vector<int>& values) {
        this->values = move(values);
        n = this->values.size();
        return dfs(0, n - 1);
    }
};

#if defined(_WIN32) || defined(__APPLE__)
/*
[3,7,4,5]

144
*/
int main() {
    string s;
    while (cin >> s) {
        vector<int> v = stringToVector(s);
        Solution sol;
        cout << sol.minScoreTriangulation(v) << endl;
    }
    return 0;
}
#endif

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

千篇源码题解已开源