决策树算法基础：信息熵相关知识

本文对信息熵等概念进行系统梳理，为后续学习决策树系列算法做好准备

挖坑待填：ID3、C4.5、CART、随机森林、LightGBM

相关文章

理解决策树模型原理，看这30页PPT就够了 - 数说新语的文章 - 知乎https://zhuanlan.zhihu.com/p/108433962

【机器学习】决策树（上）------ID3、C4.5、CART（非常详细） - 阿泽的文章 - 知乎https://zhuanlan.zhihu.com/p/85731206

一、信息熵

1.1、度量公式

【信息量】

如何量化信息？理想的度量标准应符合以下直觉：

信息量不能为负数：任何事件都是"有信息的"
信息量之间可以相加：已知事件A、事件B，两者的信息量可以累加
信息量应该随着概率单调递减：越容易发生（概率大小）的事件信息量越少，例如"明天会刮台风"相比于"明天太阳从东边升起"，就包含更多的信息
信息量应该连续依赖于概率：事件A、事件B发生概率相近，两者的信息量也接近

1928年，哈特莱给出了信息量的度量公式（满足以上要求）：事件发生概率的倒数的对数（底数为2）
I = l o g 2 1 P = − l o g 2 P I=log_2{\frac{1}{P}}=-log_2 P I=log2P1=−log2P

【信息熵】

信息熵是衡量一个概率分布所蕴含的"不确定性"的期望值 ，综合考虑了事件发生概率及事件的信息量，公式如下（对于离散型变量）：
H ( I ) = − ∑ p i l o g 2 p i H(I) = -\sum p_i log_2 p_i H(I)=−∑pilog2pi

− p i l o g 2 p i -p_ilog_{2}p_i −pilog2pi为事件发生概率与事件信息量的乘积，表示单个事件 i i i发生时，对整体不确定性的"平均贡献"
− ∑ p i l o g 2 p i -\sum p_i log_{2}p_i −∑pilog2pi为所有可能事件 i i i的贡献之和，表示整个随机变量 I I I的平均不确定性 ，即信息熵 H ( I ) H(I) H(I)

H ( I ) ≥ 0 H(I)\ge 0 H(I)≥0，且值越大，说明不确定性越高（越"混乱"）

最小值：仅有1种事件会发生，即 p i = 1 p_i=1 pi=1，其余为0，此时 H ( I ) = 0 H(I)=0 H(I)=0（规定 0 l o g 2 0 = 0 0log_2 0=0 0log20=0）
最大值 ：所有事件发生的概率相等，即 p i = 1 N p_i=\frac{1}{N} pi=N1，此时 H ( I ) = l o g 2 N H(I)=log_2 N H(I)=log2N
举例说明：袋子中共3个球（可能为红绿蓝3种颜色），取一次球，计算所取球颜色的信息熵
- 最小值：若袋子中只有红色球，则 p r e d = 1 , H ( I ) = 0 p_{red}=1, H(I)=0 pred=1,H(I)=0
- 最大值：若袋子中红绿蓝球各一个，则 H ( I ) = − 3 ∗ 1 3 ∗ l o g 2 1 3 = l o g 2 3 H(I)=-3*\frac{1}{3}*log_2 \frac{1}{3}=log_2 3 H(I)=−3∗31∗log231=log23

1.2、最大值证明

对于 H ( I ) = − ∑ i = 1 N p i l o g 2 p i H(I) = -\sum_{i=1}^{N} p_i log_2 p_i H(I)=−∑i=1Npilog2pi，满足 0 ≤ p i ≤ 1 , ∑ i = 1 N p i = 1 0\le p_i\le 1, \sum_{i=1}^N p_i=1 0≤pi≤1,∑i=1Npi=1，则 H ( I ) H(I) H(I)的最大值为 l o g 2 N log_2 N log2N

1.2.1、拉格朗日乘子法

利用拉格朗日乘子法构造函数： G ( p i , λ ) = − ∑ i = 1 N p i l o g 2 p i + λ ( ∑ i = 1 N p i − 1 ) G(p_i, \lambda)=-\sum_{i=1}^{N} p_i log_2 p_i+\lambda(\sum_{i=1}^N p_i-1) G(pi,λ)=−∑i=1Npilog2pi+λ(∑i=1Npi−1)

分别对 p i p_i pi和 λ \lambda λ求偏导： ∂ G ∂ p i = − l o g 2 p i − 1 + λ , ∂ G ∂ λ = ∑ i = 1 N p i − 1 \frac{\partial G}{\partial p_i}=-log_2 p_i-1+\lambda, \frac{\partial G}{\partial \lambda}=\sum_{i=1}^N p_i-1 ∂pi∂G=−log2pi−1+λ,∂λ∂G=∑i=1Npi−1

令 ∂ G ∂ p i = 0 \frac{\partial G}{\partial p_i}=0 ∂pi∂G=0且 ∂ G ∂ λ = 0 \frac{\partial G}{\partial \lambda}=0 ∂λ∂G=0，则 p i = 2 λ − 1 , ∑ i = 1 N p i = 1 p_i=2^{\lambda-1}, \sum_{i=1}^N p_i=1 pi=2λ−1,∑i=1Npi=1

即 p 1 = p 2 = . . . p N = 1 N p_1=p_2=...p_N=\frac{1}{N} p1=p2=...pN=N1时，函数 H ( I ) H(I) H(I)为极值，因为 H ( I ) H(I) H(I)为凹函数，则为最大值（ − ∑ i = 1 N 1 N l o g 2 1 N = − l o g 2 1 N = l o g 2 N -\sum_{i=1}^{N} \frac{1}{N} log_2 \frac{1}{N}=-log_2\frac{1}{N}=log_2 N −∑i=1NN1log2N1=−log2N1=log2N）

说明：当某个 p i = 1 p_i=1 pi=1，其余为0时，为边界点，此时 H ( X ) = 0 H(X)=0 H(X)=0（规定 0 l o g 2 0 = 0 0log_2 0=0 0log20=0），小于 l o g 2 N log_2 N log2N

拉格朗日乘子法相关链接（几何意义）：

如何理解拉格朗日乘子法？ - 马同学的回答 - 知乎https://www.zhihu.com/question/38586401/answer/457058079

如何理解拉格朗日乘子法？ - 戏言玩家的回答 - 知乎https://www.zhihu.com/question/38586401/answer/105588901

如何理解拉格朗日乘子法？ - 卢健龙的回答 - 知乎https://www.zhihu.com/question/38586401/answer/105273125

1.2.2、基于KL散度的非负性

D K L ( P ∣ ∣ Q ) = ∑ i = 1 N p i l o g 2 ( p i q i ) ≥ 0 D_{KL}(P||Q)=\sum_{i=1}^N p_i log_2 (\frac{p_i}{q_i}) \ge 0 DKL(P∣∣Q)=i=1∑Npilog2(qipi)≥0

其中， p i p_i pi、 q i q_i qi是分布 P P P和 Q Q Q在事件 i i i上的概率

设 Q Q Q为均匀分布 ，即 q i = 1 N q_i=\frac{1}{N} qi=N1

则 D K L ( P ∣ ∣ Q ) = ∑ i = 1 N p i l o g 2 ( p i 1 / N ) = ∑ i = 1 N p i l o g 2 ( p i N ) = ∑ i = 1 N p i l o g 2 p i + ∑ i = 1 N p i l o g 2 N = ∑ i = 1 N p i l o g 2 p i + l o g 2 N ∑ i = 1 N p i D_{KL}(P||Q)=\sum_{i=1}^N p_i log_2 (\frac{p_i}{1/N})=\sum_{i=1}^N p_i log_2 (p_i N)=\sum_{i=1}^N p_i log_2 p_i + \sum_{i=1}^N p_i log_2 N=\sum_{i=1}^N p_i log_2 p_i + log_2 N\sum_{i=1}^N p_i DKL(P∣∣Q)=∑i=1Npilog2(1/Npi)=∑i=1Npilog2(piN)=∑i=1Npilog2pi+∑i=1Npilog2N=∑i=1Npilog2pi+log2N∑i=1Npi

因为 ∑ i = 1 N p i = 1 \sum_{i=1}^N p_i=1 ∑i=1Npi=1，所以 D K L ( P ∣ ∣ Q ) = ∑ i = 1 N p i l o g 2 p i + l o g 2 N D_{KL}(P||Q)=\sum_{i=1}^N p_i log_2 p_i + log_2 N DKL(P∣∣Q)=∑i=1Npilog2pi+log2N

应用非负性 ，则 D K L ( P ∣ ∣ Q ) = ∑ i = 1 N p i l o g 2 p i + l o g 2 N ≥ 0 D_{KL}(P||Q)=\sum_{i=1}^N p_i log_2 p_i + log_2 N \ge 0 DKL(P∣∣Q)=∑i=1Npilog2pi+log2N≥0

可得 − ∑ i = 1 N p i l o g 2 p i ≤ l o g 2 N -\sum_{i=1}^N p_i log_2 p_i \le log_2 N −∑i=1Npilog2pi≤log2N

因此 H ( I ) ≤ l o g 2 N H(I)\le log_2 N H(I)≤log2N 得证

等号成立 ，当且仅当 ∀ i , p i = q i = 1 N \forall i, p_i=q_i=\frac{1}{N} ∀i,pi=qi=N1

二、交叉熵与KL散度（相对熵）

2.1、交叉熵

信息熵是衡量一个概率分布所蕴含的"不确定性"的期望值，交叉熵就是用一个预测分布度量真实分布所蕴含的"不确定性"的期望值 ，即在真实分布 P P P的情况下，用预测分布 Q Q Q度量信息量时的平均信息量。对于离散随机变量，其公式如下：

H ( P , Q ) = − ∑ i = 1 N p i l o g 2 q i H(P,Q) = -\sum_{i=1}^N p_i log_2 q_i H(P,Q)=−i=1∑Npilog2qi

其中， p i p_i pi、 q i q_i qi是分布 P P P和 Q Q Q在事件 i i i上的概率

举例说明（详见文章1中 "2.3 熵的估计部分" ）：预测天气

天气的真实概率分布 P P P未知，使用模型 Q Q Q进行预测（预估的概率分布）
若只考虑模型 P P P，信息熵 H ( P ) H(P) H(P)表示天气预测所需的平均信息量（也是最低信息量）；
若只考虑模型 Q Q Q，信息熵 H ( Q ) H(Q) H(Q)式中的"概率"及"信息量"均"未知"
假设经过观测后，得到了真实概率分布 P P P（将观测分布作为真实分布，详见 文章3 对于最大似然估计与交叉熵的说明），则 H ( P , Q ) H(P,Q) H(P,Q)表示真实分布 P P P的情况下，用预测分布 Q Q Q预测天气时，所需的平均信息量

性质： H ( P , Q ) ≥ H ( P ) H(P,Q)\ge H(P) H(P,Q)≥H(P)

等号成立当且仅当 P = Q P=Q P=Q，即 ∀ i , p i = q i \forall i, p_i=q_i ∀i,pi=qi（同样可采用拉格朗日乘子法证明）
可以认为信息熵 H ( P ) H(P) H(P)表示天气预测所需的最低信息量，而交叉熵 H ( P , Q ) H(P,Q) H(P,Q)表示基于预测模型 Q Q Q要付出的信息量，额外付出的信息量就是相对熵 D K L ( P ∣ ∣ Q ) D_{KL}(P||Q) DKL(P∣∣Q)

【交叉熵相关文章】

一文搞懂熵(Entropy),交叉熵(Cross-Entropy) - 将为帅的文章 - 知乎https://zhuanlan.zhihu.com/p/149186719

深入理解KL散度（番外篇一） - zjc的文章 - 知乎https://zhuanlan.zhihu.com/p/1923892456325380081

为什么交叉熵（cross-entropy）可以用于计算代价？ - 灵剑的回答 - 知乎https://www.zhihu.com/question/65288314/answer/849294209

说明：文章3中关于 P P P、 Q Q Q、观测分布的讨论

文章中观点：对数里面那个分布理解为真实的随机变量分布，而将对数外面那个理解为观察到的频率

疑问：很多文章里都把对数里面的分布Q当作预测的分布，对数外面的分布P当作真实分布，那么是否可以把观测分布当作真实分布？

回答：对于最优化问题，我们是认为优化完成的时候模型输出的恰好就是真实的概率，这是我们期望得到的结果。于是我们认为对应似然值越高说明模型效果越好，所以优化目标就变成让似然值最高，也就是让交叉熵尽量低。

2.2、KL散度（相对熵）

2.2.1、定义及性质

KL散度（Kullback-Leibler Divergence），也称相对熵（Relative Entropy），可以度量两个概率分布 P P P和 Q Q Q的差异。对于离散随机变量（包含 N N N个事件），其公式如下：
D K L ( P ∣ ∣ Q ) = ∑ i = 1 N p i l o g 2 ( p i q i ) D_{KL}(P||Q)=\sum_{i=1}^N p_i log_2 (\frac{p_i}{q_i}) DKL(P∣∣Q)=i=1∑Npilog2(qipi)

其中， p i p_i pi、 q i q_i qi是分布 P P P和 Q Q Q在事件 i i i上的概率
l o g 2 p i q i = l o g 2 p i − l o g 2 q i log_2 \frac{p_i}{q_i}=log_2 p_i - log_2 q_i log2qipi=log2pi−log2qi，可以认为是事件 i i i在不同分布下的信息量之差，如果把 P P P当作真实分布， Q Q Q当作拟合分布，则该式表示对于事件 i i i，模型 Q Q Q相对于真实情况 P P P的预测偏差所带来的信息损失
D K L ( P ∣ ∣ Q ) = ∑ i = 1 N p i l o g 2 ( p i q i ) = ∑ i = 1 N p i ( l o g 2 p i − l o g 2 q i ) D_{KL}(P||Q)=\sum_{i=1}^N p_i log_2 (\frac{p_i}{q_i})=\sum_{i=1}^N p_i(log_2 p_i - log_2 q_i) DKL(P∣∣Q)=∑i=1Npilog2(qipi)=∑i=1Npi(log2pi−log2qi)，如果把 P P P当作真实分布， Q Q Q当作拟合分布，则该式表示用分布 Q Q Q拟合分布 P P P时，分布 P P P所有可能发生事件的信息损失的期望值，即平均信息损失
D K L ( P ∣ ∣ Q ) = ∑ i = 1 N p i ( l o g 2 p i − l o g 2 q i ) = ∑ i = 1 N p i l o g 2 p i − ∑ i = 1 N p i l o g 2 q i = − ∑ i = 1 N p i l o g 2 q i − ( − ∑ i = 1 N p i l o g 2 p i ) = H ( P , Q ) − H ( P ) D_{KL}(P||Q)=\sum_{i=1}^N p_i(log_2 p_i - log_2 q_i)=\sum_{i=1}^N p_i log_2 p_i - \sum_{i=1}^N p_i log_2 q_i=- \sum_{i=1}^N p_i log_2 q_i - (-\sum_{i=1}^N p_i log_2 p_i)=H(P,Q) - H(P) DKL(P∣∣Q)=∑i=1Npi(log2pi−log2qi)=∑i=1Npilog2pi−∑i=1Npilog2qi=−∑i=1Npilog2qi−(−∑i=1Npilog2pi)=H(P,Q)−H(P)
- D K L ( P ∣ ∣ Q ) = H ( P , Q ) − H ( P ) D_{KL}(P||Q)=H(P,Q)-H(P) DKL(P∣∣Q)=H(P,Q)−H(P)，散度等于交叉熵与信息熵之差，如果把 P P P当作真实分布， Q Q Q当作拟合分布，则散度表示用分布 Q Q Q近似分布 P P P时多付出的冗余信息量，直接量化了两个分布的差异

非负性 ： D K L ( P ∣ ∣ Q ) ≥ 0 D_{KL}(P||Q)\ge 0 DKL(P∣∣Q)≥0

等号成立当且仅当 P = Q P=Q P=Q，即 ∀ i , p i = q i \forall i, p_i=q_i ∀i,pi=qi
KL散度用来衡量两个分布之间的差异程度，两者差异越小，KL散度越小，当两分布一致时，KL散度为0

不对称性 ： D K L ( P ∣ ∣ Q ) ≠ D K L ( Q ∣ ∣ P ) D_{KL}(P||Q)\neq D_{KL}(Q||P) DKL(P∣∣Q)=DKL(Q∣∣P)

【KL散度不对称性相关文章】

深入理解 KL 散度（Kullback-Leibler Divergence）：从直觉、数学到前沿应用的全方位解析 - Laurie的文章 - 知乎https://zhuanlan.zhihu.com/p/1950257135775642370

机器学习中的散度 - Taylor Wu的文章 - 知乎https://zhuanlan.zhihu.com/p/45131536

深入理解KL散度（番外篇一） - zjc的文章 - 知乎https://zhuanlan.zhihu.com/p/1923892456325380081

说明：可将文章1中 "4. 关键特性：为何它不是"距离"？ " 所举例子与文章2中 "1. 熵 vs. KL-散度" 的示例图对照理解

2.2.2、非负性证明

说明：使用Jensen不等式证明非负性

已知 D K L ( P ∣ ∣ Q ) = ∑ i = 1 N p i l o g 2 ( p i q i ) D_{KL}(P||Q)=\sum_{i=1}^N p_i log_2 (\frac{p_i}{q_i}) DKL(P∣∣Q)=∑i=1Npilog2(qipi)，即 D K L ( P ∣ ∣ Q ) = − ∑ i = 1 N p i l o g 2 ( q i p i ) D_{KL}(P||Q)=-\sum_{i=1}^N p_i log_2 (\frac{q_i}{p_i}) DKL(P∣∣Q)=−∑i=1Npilog2(piqi)

已知对数函数是凹函数（二阶导数为负），满足Jensen不等式，即 l o g 2 ( ∑ i = 1 n λ i x i ) ≥ ∑ i = 1 n λ i l o g 2 ( x i ) log_2 (\sum_{i=1}^n\lambda_i x_i)\ge \sum_{i=1}^n\lambda_i log_2 (x_i) log2(∑i=1nλixi)≥∑i=1nλilog2(xi)

将 p i p_i pi看作 λ i \lambda_i λi， q i p i \frac{q_i}{p_i} piqi看作 x i x_i xi，其中， ∀ p i , p i ≥ 0 \forall p_i, p_i \ge 0 ∀pi,pi≥0且 ∑ i = 1 n p i = 1 \sum_{i=1}^n p_i=1 ∑i=1npi=1（另外， ∑ i = 1 n q i = 1 \sum_{i=1}^n q_i=1 ∑i=1nqi=1）

则 D K L ( P ∣ ∣ Q ) = − ∑ i = 1 N p i l o g 2 ( q i p i ) ≥ l o g 2 ( ∑ i = 1 n p i q i p i ) = l o g 2 ( ∑ i = 1 n q i ) = 0 D_{KL}(P||Q)=-\sum_{i=1}^N p_i log_2 (\frac{q_i}{p_i})\ge log_2 (\sum_{i=1}^n p_i \frac{q_i}{p_i})=log_2 (\sum_{i=1}^n q_i)=0 DKL(P∣∣Q)=−∑i=1Npilog2(piqi)≥log2(∑i=1npipiqi)=log2(∑i=1nqi)=0，得证

D K L ( P ∣ ∣ Q ) = 0 D_{KL}(P||Q)=0 DKL(P∣∣Q)=0，当且仅当所有 q i p i = c \frac{q_i}{p_i}=c piqi=c，即所有的 q i = p i = 1 N q_i=p_i=\frac{1}{N} qi=pi=N1

2.3、Jensen不等式

2.3.1、凸函数与凹函数

【定义】

函数 f f f是定义区间上凸函数：如果对于区间内任意两点 x 1 x_1 x1、 x 2 x_2 x2和任意实数 λ ∈ [ 0 , 1 ] \lambda \in [0,1] λ∈[0,1]，都有以下不等式成立：
f ( λ x 1 + ( 1 − λ ) x 2 ) ≤ λ f ( x 1 ) + ( 1 − λ ) f ( x 2 ) f(\lambda x_1 + (1-\lambda) x_2) \le \lambda f(x_1) + (1-\lambda) f(x_2) f(λx1+(1−λ)x2)≤λf(x1)+(1−λ)f(x2)

【说明】

不等式中的" ≤ \le ≤"换成" < < <"，则称函数为严格凸函数
λ x 1 + ( 1 − λ ) x 2 \lambda x_1 + (1-\lambda) x_2 λx1+(1−λ)x2：表示 x 1 x_1 x1、 x 2 x_2 x2的一个凸组合，实际上就是连接 x 1 x_1 x1、 x 2 x_2 x2的线段上的任意一点
λ f ( x 1 ) + ( 1 − λ ) f ( x 2 ) \lambda f(x_1) + (1-\lambda) f(x_2) λf(x1)+(1−λ)f(x2)：表示函数值 f ( x 1 ) f(x_1) f(x1)、 f ( x 2 ) f(x_2) f(x2)的一个凸组合，实际上就是弦（两点连线）上对应点的值

【凸组合说明】

λ x 1 + ( 1 − λ ) x 2 = x 2 − λ ( x 2 − x 1 ) \lambda x_1 + (1-\lambda) x_2=x_2-\lambda(x_2-x_1) λx1+(1−λ)x2=x2−λ(x2−x1)

λ = 0 \lambda=0 λ=0时： x 2 − λ ( x 2 − x 1 ) = x 2 x_2-\lambda(x_2-x_1)=x_2 x2−λ(x2−x1)=x2
λ = 1 \lambda=1 λ=1时： x 2 − λ ( x 2 − x 1 ) = x 1 x_2-\lambda(x_2-x_1)=x_1 x2−λ(x2−x1)=x1
0 < λ < 1 0<\lambda<1 0<λ<1时： x 2 − λ ( x 2 − x 1 ) x_2-\lambda(x_2-x_1) x2−λ(x2−x1)表示 x 1 x_1 x1、 x 2 x_2 x2之间的任意一点
λ \lambda λ越大，点越靠近 x 1 x_1 x1（为方便理解，可以 0 < x 1 < x 2 0<x_1<x_2 0<x1<x2为例进行分析，此时 x 2 − x 1 x_2-x_1 x2−x1表示两点之间的距离）

【几何意义】

凸函数意味着弦始终在函数图像 的上方

2.3.2、Jensen不等式

函数 ϕ \phi ϕ是定义区间上的凹函数 ：对于任意点 x 1 , x 2 , . . . , x n ∈ I x_1, x_2,..., x_n \in I x1,x2,...,xn∈I和权重 λ 1 , λ 2 , . . . , λ n ≥ 0 \lambda_1, \lambda_2,..., \lambda_n \ge 0 λ1,λ2,...,λn≥0满足 ∑ i = 1 n λ i = 1 \sum_{i=1}^n \lambda_i=1 ∑i=1nλi=1，有：
ϕ ( ∑ i = 1 n λ i x i ) ≥ ∑ i = 1 n λ i ϕ ( x i ) \phi(\sum_{i=1}^n\lambda_i x_i)\ge \sum_{i=1}^n\lambda_i \phi(x_i) ϕ(i=1∑nλixi)≥i=1∑nλiϕ(xi)

若函数 ϕ \phi ϕ是严格凹函数 ，则等号成立当且仅当 所有 x i x_i xi（对应权重 λ i > 0 \lambda_i>0 λi>0）完全相等 ，即 x 1 = x 2 = . . . x n x_1=x_2=...x_n x1=x2=...xn

【取等条件证明】

【充分性】：若所有 x i x_i xi相等（设 x i = c x_i=c xi=c），则 ϕ ( ∑ i = 1 n λ i x i ) = ∑ i = 1 n λ i ϕ ( x i ) \phi(\sum_{i=1}^n\lambda_i x_i)=\sum_{i=1}^n\lambda_i \phi(x_i) ϕ(∑i=1nλixi)=∑i=1nλiϕ(xi)

若所有 x i x_i xi相等（设 x i = c x_i=c xi=c），则：

ϕ ( ∑ i = 1 n λ i x i ) = ϕ ( c ∑ i = 1 n λ i ) = ϕ ( c ) \phi(\sum_{i=1}^n\lambda_i x_i)=\phi(c\sum_{i=1}^n\lambda_i)=\phi(c) ϕ(∑i=1nλixi)=ϕ(c∑i=1nλi)=ϕ(c)
∑ i = 1 n λ i ϕ ( x i ) = ∑ i = 1 n λ i ϕ ( c ) = ϕ ( c ) \sum_{i=1}^n\lambda_i \phi(x_i)=\sum_{i=1}^n\lambda_i \phi(c)=\phi(c) ∑i=1nλiϕ(xi)=∑i=1nλiϕ(c)=ϕ(c)
等式成立

【必要性】：若 ϕ ( ∑ i = 1 n λ i x i ) = ∑ i = 1 n λ i ϕ ( x i ) \phi(\sum_{i=1}^n\lambda_i x_i)=\sum_{i=1}^n\lambda_i \phi(x_i) ϕ(∑i=1nλixi)=∑i=1nλiϕ(xi)，则所有 x i x_i xi相等

已知条件：函数 ϕ \phi ϕ是严格凹函数，即 ϕ ( λ x 1 + ( 1 − λ ) x 2 ) > λ ϕ ( x 1 ) + ( 1 − λ ) ϕ ( x 2 ) \phi(\lambda x_1 + (1-\lambda) x_2) > \lambda \phi(x_1) + (1-\lambda) \phi(x_2) ϕ(λx1+(1−λ)x2)>λϕ(x1)+(1−λ)ϕ(x2)

假设 ϕ ( ∑ i = 1 n λ i x i ) = ∑ i = 1 n λ i ϕ ( x i ) \phi(\sum_{i=1}^n\lambda_i x_i)=\sum_{i=1}^n\lambda_i \phi(x_i) ϕ(∑i=1nλixi)=∑i=1nλiϕ(xi)，但存在 x j ≠ x k x_j \neq x_k xj=xk（对应权重 λ j > 0 , λ k > 0 \lambda_j>0, \lambda_k>0 λj>0,λk>0），将点集分为两组：

组A：与 x j x_j xj相同的点（权重和 α = ∑ i ∈ A λ i > 0 \alpha=\sum_{i\in A}\lambda_i>0 α=∑i∈Aλi>0）
组B：其他点（权重和 β = ∑ i ∈ B λ i > 0 \beta=\sum_{i\in B}\lambda_i>0 β=∑i∈Bλi>0含 x k x_k xk）， α + β = 1 \alpha+\beta=1 α+β=1
两组的加权平均值分别记为： y = ∑ i ∈ A λ i x i α = x j y=\frac{\sum_{i\in A}\lambda_i x_i}{\alpha}=x_j y=α∑i∈Aλixi=xj， z = ∑ i ∈ B λ i x i β z=\frac{\sum_{i\in B}\lambda_i x_i}{\beta} z=β∑i∈Bλixi
则 ϕ ( ∑ i = 1 n λ i x i ) = ϕ ( α y + β z ) \phi(\sum_{i=1}^n\lambda_i x_i)=\phi(\alpha y + \beta z) ϕ(∑i=1nλixi)=ϕ(αy+βz)，为严格凹函数，当 y ≠ z y\neq z y=z时可推出 ϕ ( α y + β z ) > α ϕ ( y ) + β ϕ ( z ) \phi(\alpha y + \beta z)>\alpha\phi(y) + \beta\phi(z) ϕ(αy+βz)>αϕ(y)+βϕ(z)
则 ∑ i = 1 n λ i ϕ ( x i ) = ∑ i ∈ A λ i ϕ ( x i ) + ∑ i ∈ B λ i ϕ ( x i ) ≤ α ϕ ( y ) + ϕ ( ∑ i ∈ B λ x i ) = α ϕ ( y ) + β ϕ ( z ) \sum_{i=1}^n\lambda_i \phi(x_i)=\sum_{i\in A}\lambda_i \phi(x_i) + \sum_{i\in B}\lambda_i \phi(x_i)\le \alpha \phi(y) + \phi(\sum_{i\in B}\lambda x_i)=\alpha \phi(y) + \beta \phi(z) ∑i=1nλiϕ(xi)=∑i∈Aλiϕ(xi)+∑i∈Bλiϕ(xi)≤αϕ(y)+ϕ(∑i∈Bλxi)=αϕ(y)+βϕ(z)
所以： ϕ ( ∑ i = 1 n λ i x i ) = ϕ ( α y + β z ) > α ϕ ( y ) + β ϕ ( z ) ≥ ∑ i = 1 n λ i ϕ ( x i ) \phi(\sum_{i=1}^n\lambda_i x_i)=\phi(\alpha y + \beta z)>\alpha\phi(y) + \beta\phi(z)\ge \sum_{i=1}^n\lambda_i \phi(x_i) ϕ(∑i=1nλixi)=ϕ(αy+βz)>αϕ(y)+βϕ(z)≥∑i=1nλiϕ(xi)

因为 ϕ ( ∑ i = 1 n λ i x i ) = ∑ i = 1 n λ i ϕ ( x i ) \phi(\sum_{i=1}^n\lambda_i x_i)=\sum_{i=1}^n\lambda_i \phi(x_i) ϕ(∑i=1nλixi)=∑i=1nλiϕ(xi)

可得 y = z y=z y=z，即 ϕ ( α y + β z ) = α ϕ ( y ) + β ϕ ( z ) \phi(\alpha y + \beta z)=\alpha\phi(y) + \beta\phi(z) ϕ(αy+βz)=αϕ(y)+βϕ(z)
可得 ∑ i ∈ B λ i ϕ ( x i ) = ϕ ( ∑ i ∈ B λ x i ) \sum_{i\in B}\lambda_i \phi(x_i)=\phi(\sum_{i\in B}\lambda x_i) ∑i∈Bλiϕ(xi)=ϕ(∑i∈Bλxi)，对组 B B B中的元素继续划分组 A A A、组 B B B，可证明所有 x i x_i xi相等

三、其他度量指标

3.1、条件熵

对于随机变量 X , Y X,Y X,Y，条件熵 H ( Y ∣ X ) H(Y|X) H(Y∣X)表示在已知随机变量 X X X的条件下随机变量 Y Y Y的不确定性
H ( Y ∣ X ) = ∑ x ∈ X p x H ( Y ∣ X = x ) = − ∑ x ∈ X p x ∑ y ∈ Y p y ∣ x l o g 2 p y ∣ x H(Y|X)=\sum_{x\in X}p_x H(Y|X=x)=-\sum_{x \in X}p_x\sum_{y \in Y}p_{y|x}log_2 p_{y|x} H(Y∣X)=x∈X∑pxH(Y∣X=x)=−x∈X∑pxy∈Y∑py∣xlog2py∣x

举例说明：

对于样本数据集 D D D，样本个数为 ∣ D ∣ |D| ∣D∣，可分为 K K K个类别， ∣ C k ∣ |C_k| ∣Ck∣表示类 C k C_k Ck的样本个数，则 ∑ k = 1 K C k = ∣ D ∣ \sum_{k=1}^K{C_k}=|D| ∑k=1KCk=∣D∣
则数据集的信息熵 H ( D ) = − ∑ k = 1 K ∣ C k ∣ ∣ D ∣ l o g 2 ∣ C k ∣ ∣ D ∣ H(D)=-\sum_{k=1}^K\frac{|C_k|}{|D|}log_2 \frac{|C_k|}{|D|} H(D)=−∑k=1K∣D∣∣Ck∣log2∣D∣∣Ck∣
设 A A A为数据集 D D D的某一个特征变量，有 n n n个不同的取值 a 1 , a 2 , . . . , a n a_1,a_2,...,a_n a1,a2,...,an，根据特征 A A A的取值，将 D D D划分为 n n n个子集 D 1 , D 2 , . . . , D n D_1,D_2,...,D_n D1,D2,...,Dn， ∣ D i ∣ |D_i| ∣Di∣表示子集 D i D_i Di的样本个数，则有 ∑ i = 1 n ∣ D i ∣ = ∣ D ∣ \sum_{i=1}^n|D_i|=|D| ∑i=1n∣Di∣=∣D∣
记子集中 D i D_i Di属于类 C k C_k Ck的样本集合为 D i k D_{ik} Dik，则 ∣ D i k ∣ |D_{ik}| ∣Dik∣为 D i k D_{ik} Dik的样本个数
则针对特征 A A A，数据集 D D D的条件熵 H ( D ∣ A ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ ∑ k = 1 K ∣ D i k ∣ ∣ D i ∣ l o g 2 ∣ D i k ∣ ∣ D i ∣ H(D|A)=-\sum_{i=1}^n\frac{|D_i|}{|D|}\sum_{k=1}^K\frac{|D_{ik}|}{|D_i|}log_2 \frac{|D_{ik}|}{|D_i|} H(D∣A)=−∑i=1n∣D∣∣Di∣∑k=1K∣Di∣∣Dik∣log2∣Di∣∣Dik∣，表示在已知特征 A A A的条件下 D D D的不确定性

【条件熵相关文章】

通俗理解条件熵 - 忆臻的文章 - 知乎https://zhuanlan.zhihu.com/p/26551798

3.2、信息增益及信息增益率

信息增益 G ( D , A ) = H ( D ) − H ( D ∣ A ) G(D,A)=H(D)-H(D|A) G(D,A)=H(D)−H(D∣A)，表示已知特征 A A A对于减少 D D D未知量的贡献

信息增益越大表示使用特征 A A A来划分所获得的"纯度提升越大"
缺点：若根据信息增益的大小确定分类特征则偏向于可取值数较多的特征，例如"编号"类的特征使得条件熵取0，信息增益最大

利用信息增益率可以克服信息增益的缺点，其公式为：
G R = G ( D , A ) H A ( D ) H A ( D ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ l o g 2 ∣ D i ∣ ∣ D ∣ G_R=\frac{G(D,A)}{H_A(D)}\\ H_A(D)=-\sum_{i=1}^n\frac{|D_i|}{|D|}log_2 \frac{|D_i|}{|D|} GR=HA(D)G(D,A)HA(D)=−i=1∑n∣D∣∣Di∣log2∣D∣∣Di∣
H A ( D ) H_A(D) HA(D)表示特征 A A A的不确定性（"不纯度"），不同取值的分布越分散，该值越大，因此可以修正"偏向于可取值数较多的特征"的缺陷，但随之而来的是对可取值较少的特征有所偏好（分母越小，整体越大）

3.3、基尼指数

与信息熵类似，基尼指数也是度量随机变量不纯度的指标，对于离散随机变量，其公式为：
G i n i ( I ) = ∑ i = 1 N p i ( 1 − p i ) = 1 − ∑ i = 1 N p i 2 Gini(I)=\sum_{i=1}^N p_i(1-p_i)=1-\sum_{i=1}^N p_i^2 Gini(I)=i=1∑Npi(1−pi)=1−i=1∑Npi2
0 ≤ G i n i ( I ) ≤ 1 0\le Gini(I)\le 1 0≤Gini(I)≤1，且值越大，说明不确定性越高（越"混乱"）

最小值：仅有1种事件会发生，即 p i = 1 p_i=1 pi=1，其余为0，此时 G i n i ( I ) = 0 Gini(I)=0 Gini(I)=0
最大值 ：所有事件发生的概率相等，即 p i = 1 N p_i=\frac{1}{N} pi=N1，此时 G i n i ( I ) = 1 − 1 N 2 Gini(I)=1-\frac{1}{N^2} Gini(I)=1−N21
信息熵的计算公式中包含大量耗时的对数运算，基尼指数在简化公式的同时性能也接近熵模型
- 对于函数 l o g 2 ( x ) log_2(x) log2(x)，一阶泰勒展开为 l o g 2 ( x ) = − 1 + x + o ( x ) log_2(x)=-1+x+o(x) log2(x)=−1+x+o(x)
- 所以 H ( X ) = − ∑ p x l o g 2 p x ≈ ∑ p x ( 1 − p x ) H(X)=-\sum p_x log_2 p_x\approx \sum p_x(1-p_x) H(X)=−∑pxlog2px≈∑px(1−px)，即基尼指数可以理解为熵模型的一阶泰勒展开

对于样本数据集 D D D， G i n i ( D ) = ∑ k = 1 K ∣ C k ∣ ∣ D ∣ ( 1 − ∣ C k ∣ ∣ D ∣ ) Gini(D)=\sum_{k=1}^K\frac{|C_k|}{|D|}(1-\frac{|C_k|}{|D|}) Gini(D)=∑k=1K∣D∣∣Ck∣(1−∣D∣∣Ck∣)

基尼指数反映了从数据集中随机抽取两个样本，其类别标记不一致的概率。因此基尼指数越小，则数据集纯度越高。
基尼指数偏向于特征值较多的特征，类似信息增益

附上一张二分类情况下，信息熵、基尼指数、分类误差的对比图

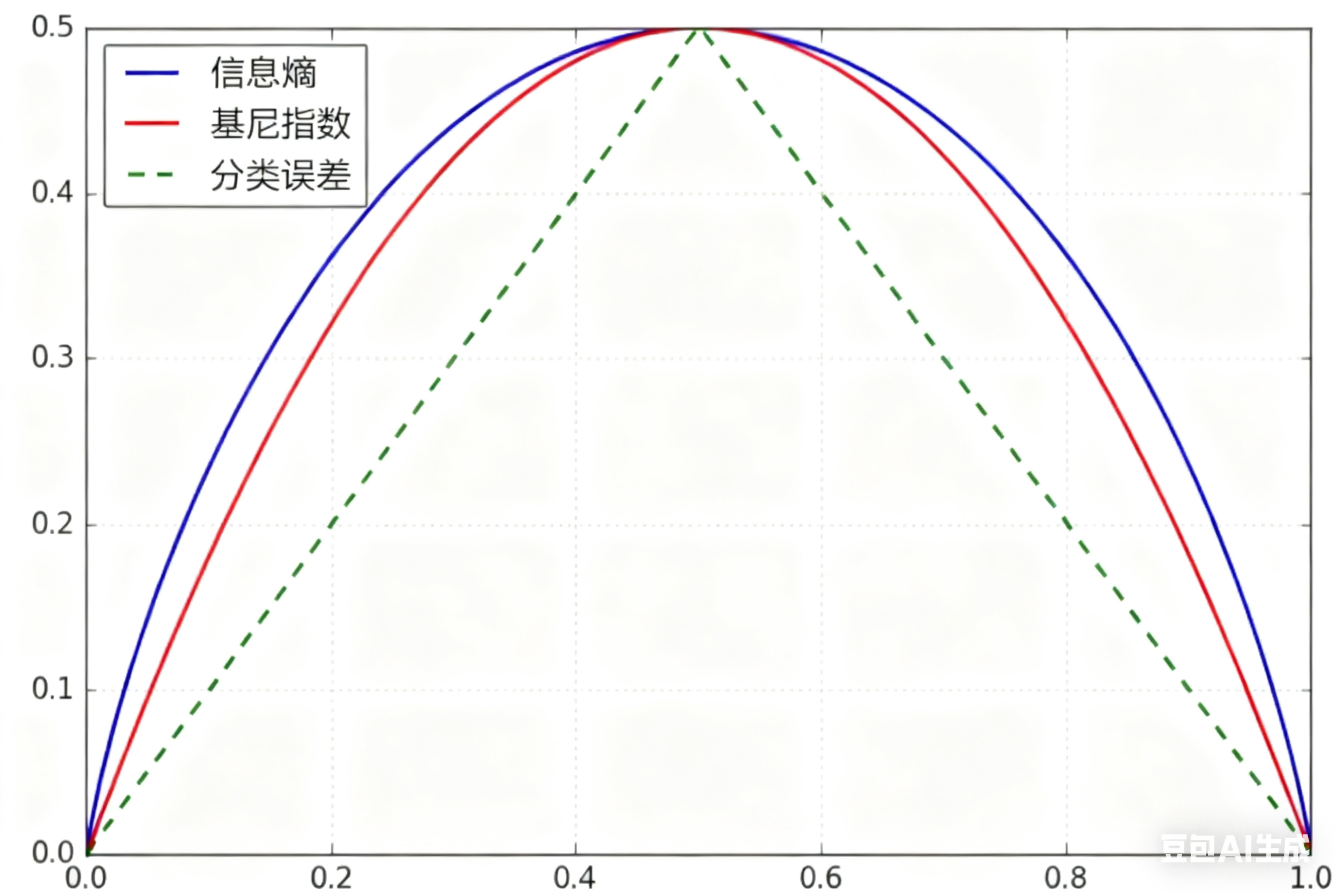
在分析Gini系数，熵，分类误差率时。其中，分类误差率具体是什么，为什么一定小于等于0.5? - 曹佳鑫的回答 - 知乎https://www.zhihu.com/question/351016937/answer/859497058