今天我们要聊聊机器学习界的一位"硬汉"------SVM (Support Vector Machine) ,中文名叫支持向量机。
名字听起来是不是有点高冷?别怕,它的核心思想其实特别简单,甚至有点像小孩子玩的游戏。
如果你完全不懂算法,没关系。想象一下,你面前有一张桌子,桌子上放着两种颜色的球:红球 🔴 和 蓝球🔵。
1. 它的任务是什么?
你的任务很简单:拿一根木棍,把红球和蓝球分开。
这听起来很容易,对吧?只要把木棍往中间一放,左边是红球,右边是蓝球,搞定!
但是,SVM 不仅仅是想"分开"它们,它想找的是最完美的那根木棍。
2. 什么是"最完美"的分界线?
假设红球和蓝球离得比较远,你可以有很多种放木棍的方法:
- 方案 A:木棍紧贴着红球放。
- 方案 B:木棍紧贴着蓝球放。
- 方案 C:木棍放在正中间。
你觉得哪个最好?
直觉告诉我们:方案 C 最好 。为什么?
因为方案 A 和 B 太"偏心"了。如果再滚来一个新的红球,稍微偏一点点,方案 A 可能就把它错分到蓝球那边去了。
SVM 的逻辑就是:
- 这根木棍(分界线)必须把两类分开。
- 这根木棍离红球最近的那几个球,和离蓝球最近的那几个球,距离要越远越好。
这就好比在木棍两边修了一条大马路 。马路越宽,我们就越有安全感,分类就越准确。
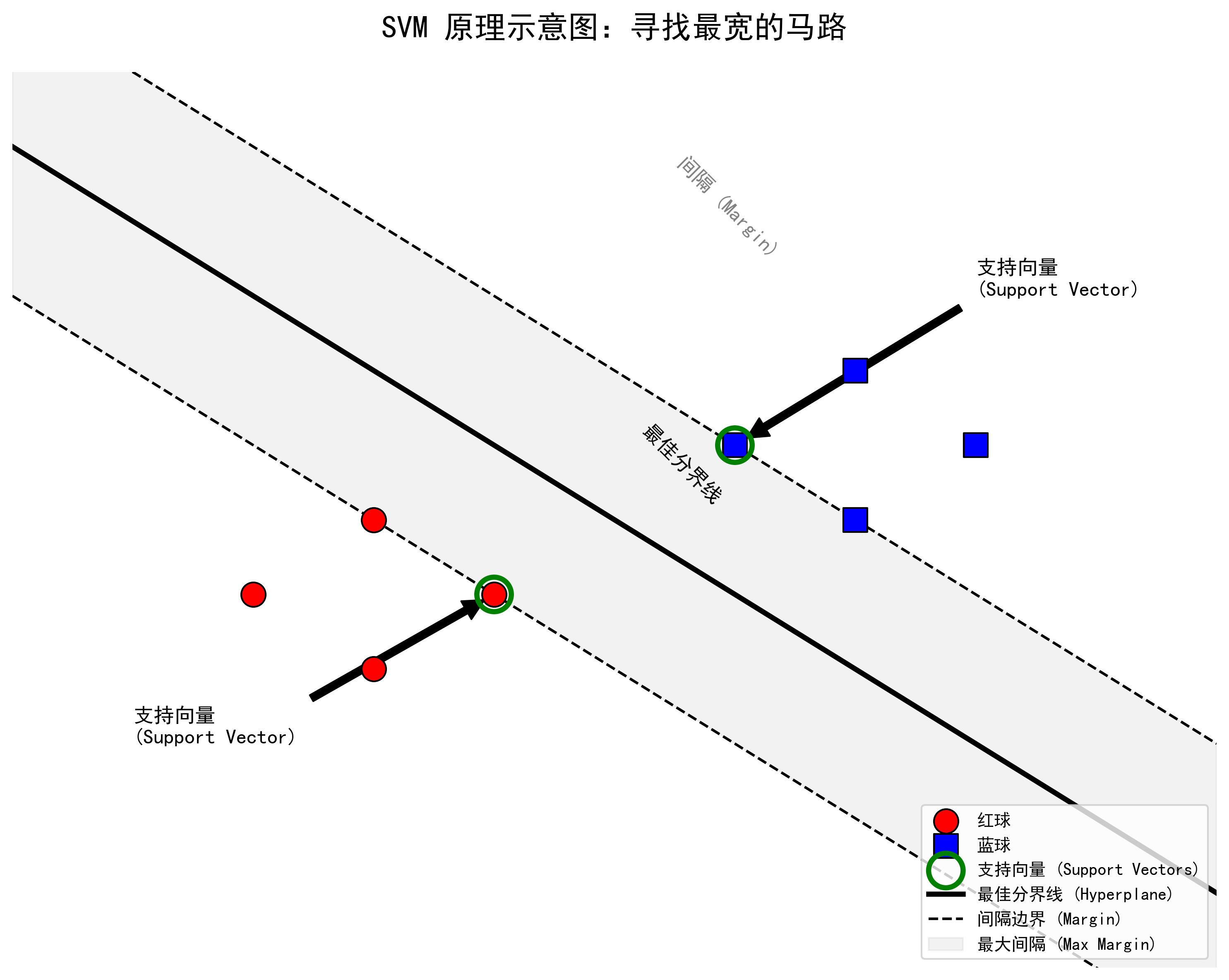
🔑 关键名词解释
- 支持向量 (Support Vectors) :就是那些离分界线最近的球。它们是"撑起"这条马路宽度的关键角色。其他的球离得远,对分界线的位置没有影响。
- 间隔 (Margin) :就是这条"马路"的宽度。SVM 的目标就是让间隔最大化。
3. 如果直线分不开怎么办?(核函数的魔法)
刚才的情况比较简单,一根直的木棍就能分开。但现实往往很残酷。
场景升级 :
假设红球在桌子正中间,蓝球围着红球摆了一圈(像一个靶子)。
这时候,无论你怎么放直木棍,都无法把红球和蓝球完全分开。怎么办?
SVM 有一个超级大招,叫做核函数 (Kernel Trick)。
想象一下,你突然有了超能力!你猛地拍了一下桌子:
- 红球因为比较轻,飞到了半空中。
- 蓝球比较重,还留在桌面上。
现在,你不再是在二维平面上看它们了,你是在三维空间里。
这时候,你拿一张平整的纸板,像切蛋糕一样,横着插进红球和蓝球之间。
- 纸板上面是红球。
- 纸板下面是蓝球。
完美分开!
当你把视角切回到原来的二维桌面时,你会发现那张平整的纸板,在桌面上变成了一个圆形的圈,刚好把红球包在里面。
这就是 SVM 的厉害之处:当低维空间分不开时,它就把数据映射到高维空间,用更高维度的"刀"来切分。
4. SVM 的优缺点
✅ 优点 (为什么它很强?)
- 数学理论完美:它不是瞎猜,而是有严格的数学证明,保证找到的是全局最优解。
- 适合小样本:不需要海量数据也能训练出很好的模型(因为它只关心那几个关键的"支持向量")。
- 能处理复杂关系:通过"核函数",它可以画出各种奇形怪状的分界线(圆的、弯的...)。
❌ 缺点 (也要注意)
- 怕大规模数据:如果数据量有几十万、上百万,SVM 算起来会非常慢,因为它要算矩阵。
- 对噪声敏感:如果红球堆里混进了一个蓝球(噪声),SVM 可能会为了强行把这个蓝球分对,而把马路修得很窄,导致整体效果变差。
5. 总结
SVM (支持向量机) 就是一个强迫症的分类员:
- 它不光要把两类东西分开。
- 它还要找一条路最宽的分界线。
- 如果直线分不开,它就升维打击,用高维空间的平面来分。
它曾经是机器学习界的王者,虽然现在深度学习很火,但在数据量不大、要求精准的场景下,SVM 依然是首选的神器!⚔️