Week09-Clustering聚类&k-mean

一、什么是Clustering

1-1、什么是聚类 (Clustering)?

假设你正在处理一个包含病人信息的医疗系统数据集。这个数据集很复杂，既有分类特征（categorical），也有数值特征（numeric）。你想要在数据中找到规律和相似性，该怎么做呢？

聚类（Clustering） 是一种 无监督机器学习技术，它会根据数据之间的相似性，把没有标签的数据分组。（如果数据本来有标签，那这种分组叫做 分类（Classification）。）

例如，一个研究人员正在进行一项临床试验，评估一种新疗法。在研究过程中，病人会汇报自己 每周出现症状的次数 和 症状的严重程度 。研究人员可以用 聚类分析 将症状表现相似的病人分成几组。

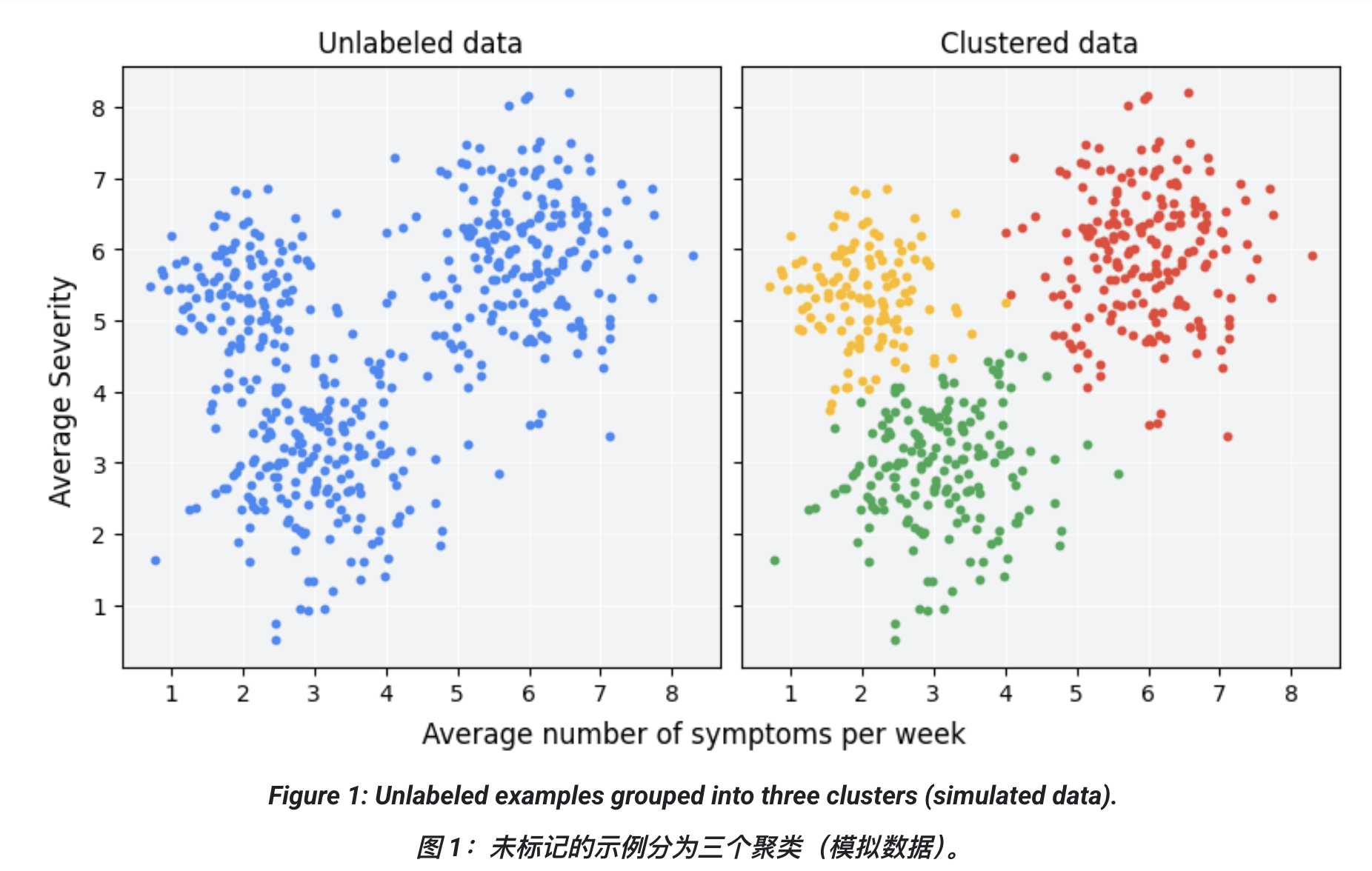
图 1 演示了如何把一组模拟数据分为三个聚类：

• 左边：散点图（横轴是症状次数，纵轴是严重程度），可以隐约看到三组点。

• 右边：同一张图，但三个聚类被不同颜色区分开来。

即使不正式计算"相似度"，人眼也能看出左边的数据大概有三个簇。

但在现实中，必须定义一个明确的 相似性度量（similarity measure），告诉算法如何比较数据点之间的相似程度。

• 当特征只有一两个时，直观上很好比较。

• 但特征维度一多，计算就变复杂了，需要合适的度量方式（如欧氏距离、余弦相似度等）。

  后续章节会介绍不同的相似性度量方法（人工定义的，或基于向量嵌入 embeddings 的）。

完成聚类后，每个分组都会有一个唯一的标签，叫做 Cluster ID。

聚类的强大之处在于：它能把庞大复杂的数据（很多特征）简化成一个 ID。

---

1-2、聚类的应用场景

聚类在很多行业都有应用：

• 市场细分（Market segmentation）

• 社交网络分析

• 搜索结果分组

• 医学影像分析

• 图像分割

• 异常检测

具体例子：

• 天文学：赫罗图 (Hertzsprung-Russell diagram)，把恒星按亮度和温度聚类。

• 生物学：基因测序揭示了不同物种之间以前未知的遗传相似性，导致分类体系的更新。

• 心理学 ：人格特质的 大五模型（Big Five） 是通过聚类分析性格词汇得出的，后来 HEXACO 模型扩展为 6 个聚类。

---

1-3、聚类的用途

1. 缺失值填补（Imputation）

   • 如果一个簇里有些样本的特征缺失，可以用同簇的其他样本推测缺失值。

   • 例如，把冷门视频和热门视频聚在一起，可以帮助改进推荐系统。

2. 数据压缩（Data compression）

   • 原始数据特征可以被聚类 ID 替代。

   • 这样减少了维度，也减少了存储、计算和训练开销。

   • 例如，一个 YouTube 视频的原始特征：

     • 用户观看位置、时间、人口统计

     • 评论时间戳、评论内容、用户 ID

     • 视频标签

       经过聚类后，可以只用一个 Cluster ID 代替所有这些特征。

3. 隐私保护（Privacy preservation）

   • 可以用聚类 ID 替代用户 ID，从而减少隐私泄露风险。

   • 比如在训练 YouTube 用户观看记录模型时，不直接用 user ID，而是用 cluster ID。

   • 这样单个用户的行为不会直接暴露。

   • 注意：每个簇里必须包含足够多用户，隐私保护才有效。

---

1-4、通俗讲解

聚类 = 给一堆没有标签的数据，自动分"群组"。

就像你走进一个派对，没名字标签，但你能根据衣着、语言，把人分成几拨：

• 一群穿西装的

• 一群穿运动服的

• 一群拿相机的

这就是聚类。

在实际数据里：

• 分类 (Classification) = 已知标签（监督学习），比如"这是不是癌症患者"。

• 聚类 (Clustering) = 没有标签（无监督学习），只能让算法找相似点，自动分组。

聚类的价值：

• 简化复杂数据（几百个特征 → 一个 cluster ID）

• 找隐藏模式（谁和谁更像）

• 还能帮助 补缺失值、压缩数据、保护隐私。

---

二、Clustering algorithms（聚类算法）

2-1、聚类算法 (Clustering algorithms)

机器学习数据集可能有数百万条样本，但不是所有的聚类算法都能高效扩展。

许多聚类算法需要计算 所有样本两两之间的相似性 ，因此运行时间复杂度会随着样本数的平方增长，即 O(n²)。这种算法在大规模数据集（百万级以上）上是不实用的。

K-means 算法 的复杂度是 O(n)，意味着它的运行时间与样本数量成线性关系。

因此，K-means 具有良好的扩展性，也是本章的重点。

---

2-2、聚类的类型 (Types of clustering)

聚类方法有很多种，不同方法适合不同的数据分布。这里介绍四种常见方法：

1. 基于质心的聚类 (Centroid-based clustering)

• 簇的质心（centroid）就是该簇所有点的算术平均值。

• 算法将数据划分为非层次性的簇。

• 优点：高效，易理解。

• 缺点：对初始条件和离群点敏感。

• 代表算法：K-means

  • 需要用户指定簇的数量 k

  • 适合"大小差不多"的簇

---

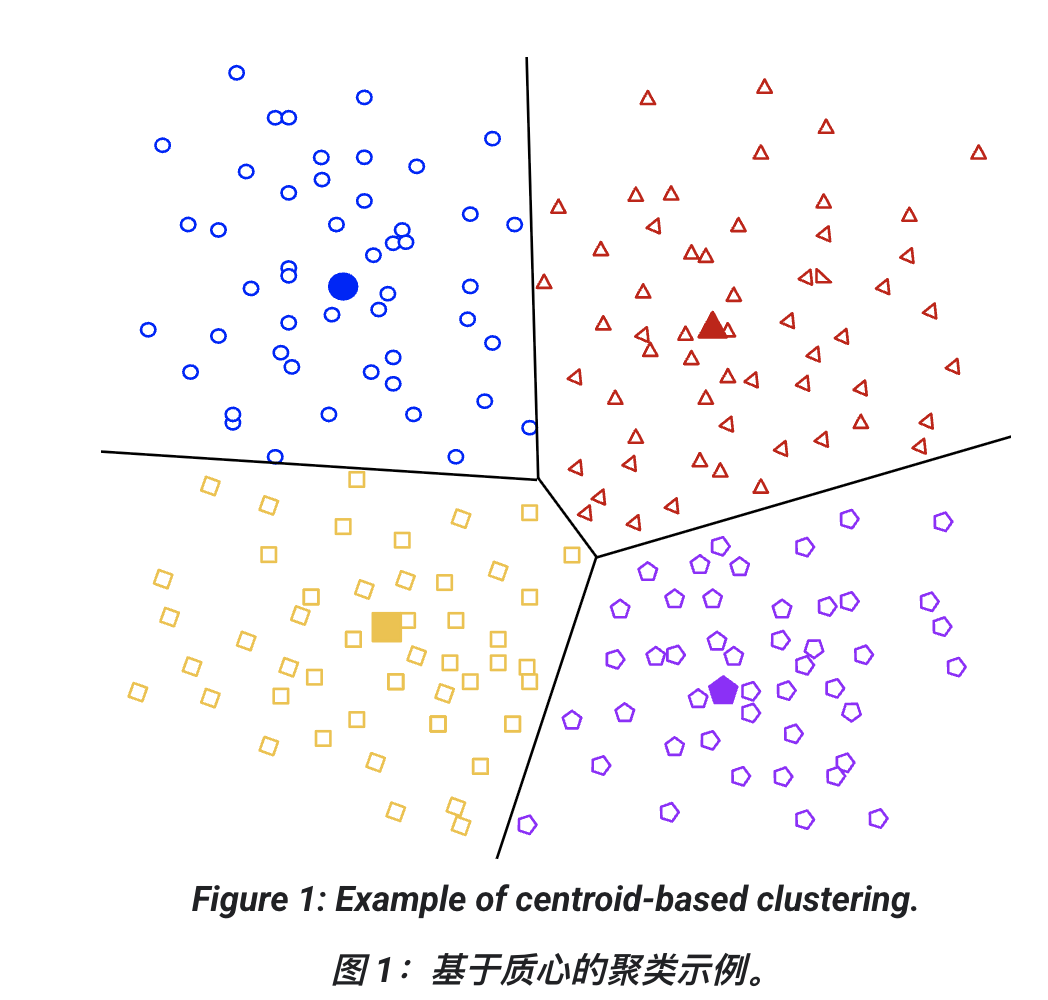
2. 基于密度的聚类 (Density-based clustering)

• 根据高密度区域的连续性形成簇。

• 能发现任意数量、任意形状的簇。

• 离群点不会分配到任何簇中。

• 缺点：

  • 对不同密度的簇效果不好

  • 在高维数据中表现不佳

• 代表算法：DBSCAN

---

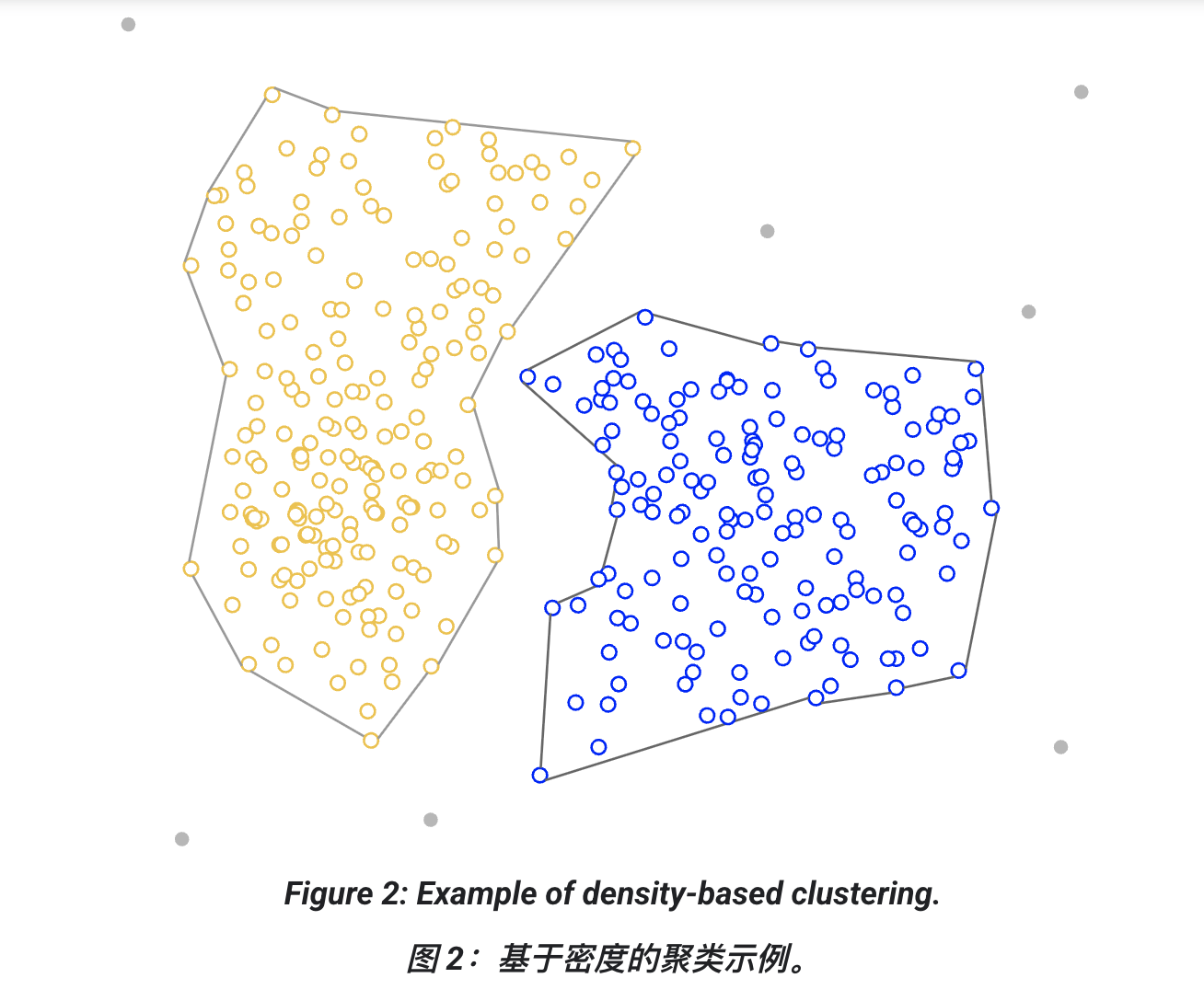
3. 基于分布的聚类 (Distribution-based clustering)

• 假设数据来自某种概率分布（如高斯分布）。

• 簇就是这些分布的混合。

• 样本离分布中心越远，它属于该簇的概率越低。

• 缺点：需要预先假设分布形式，不适合分布未知的情况。

• 代表算法：高斯混合模型 (Gaussian Mixture Model, GMM)

---

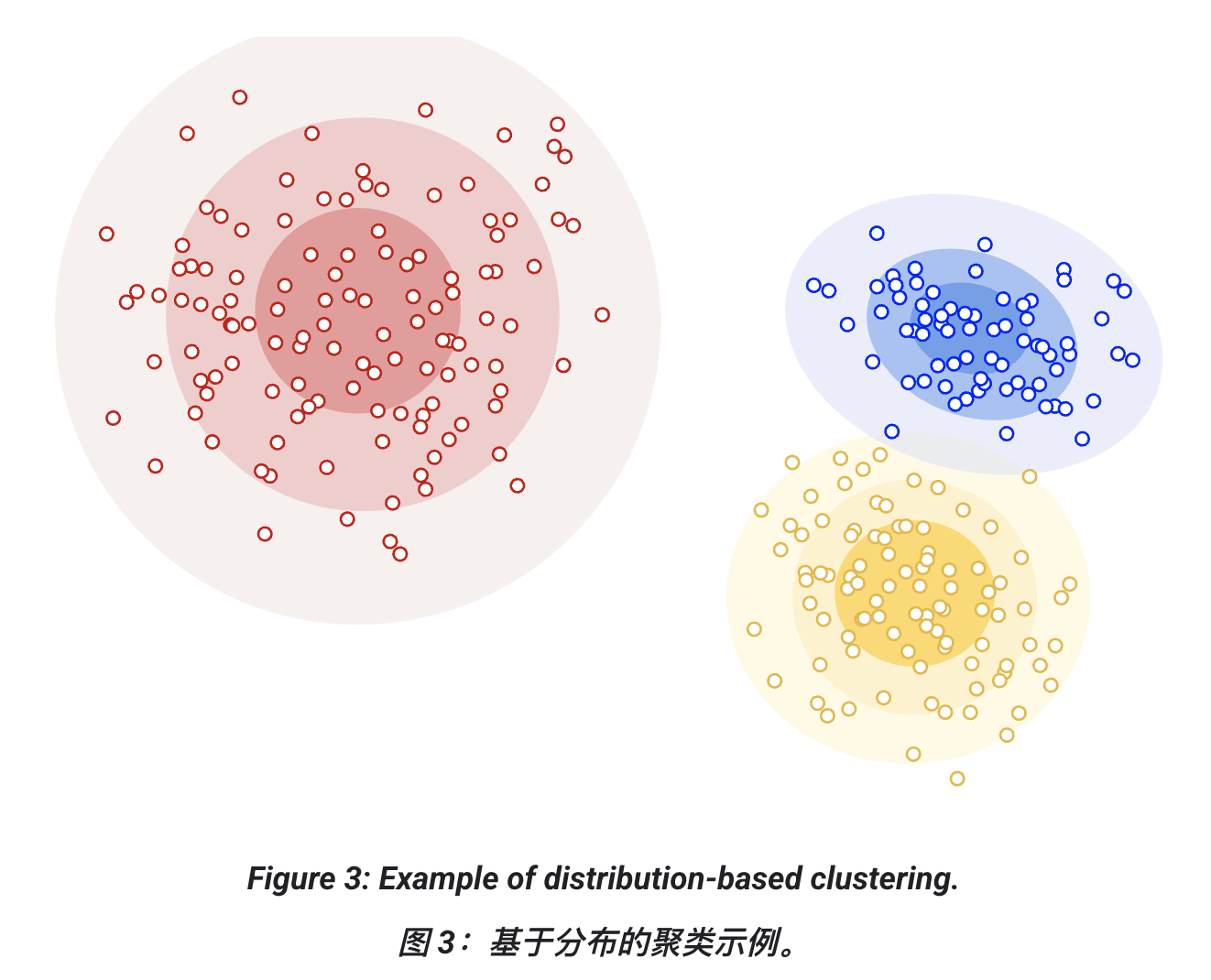
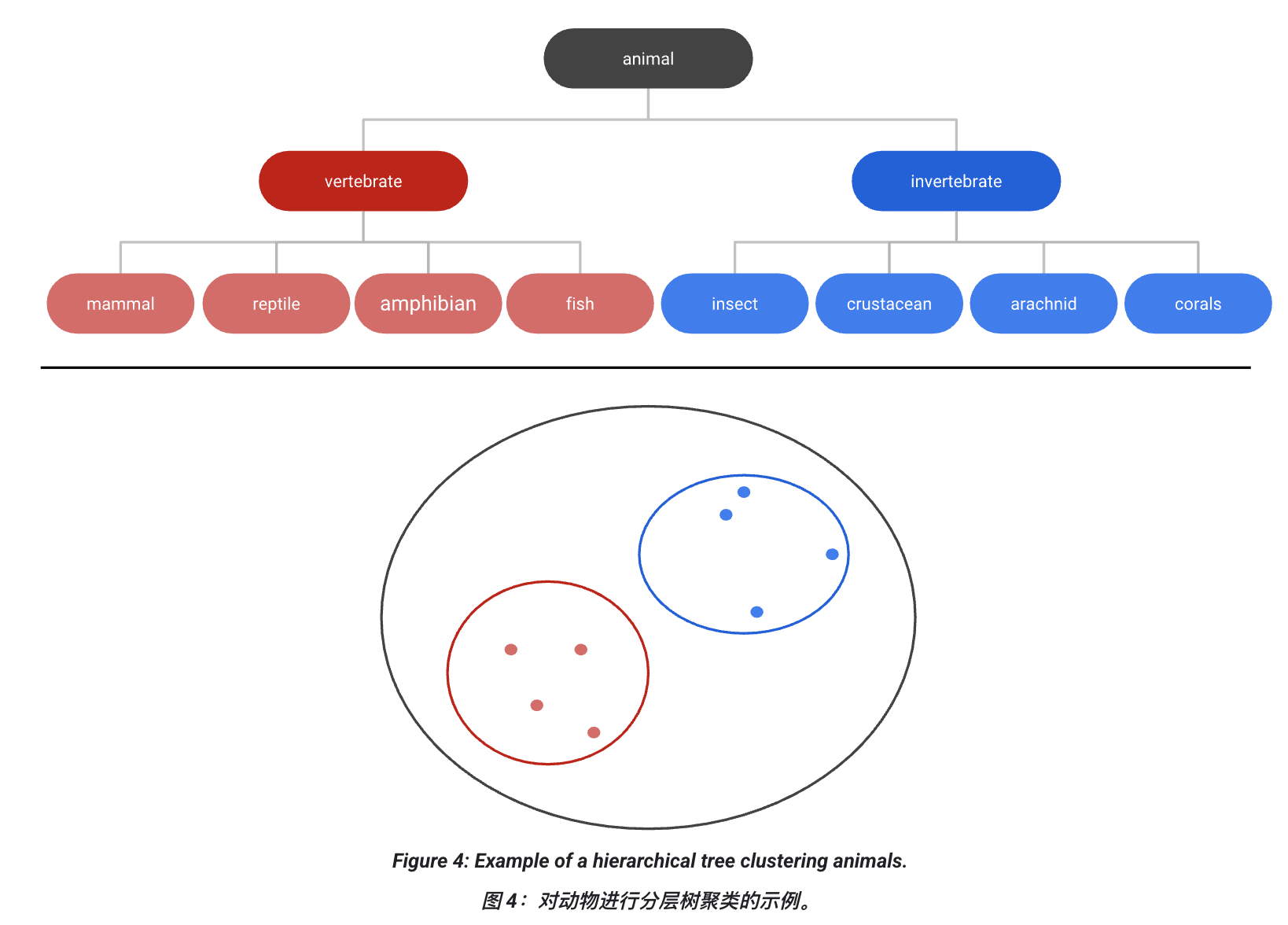
4. 层次聚类 (Hierarchical clustering)

• 生成一个簇的树状结构（dendrogram）。

• 适合层次性数据（如生物分类学）。

• 可以通过在合适的层级"剪树"得到任意数量的簇。

---

2-3、通俗讲解

你可以把这四种方法想象成"分组策略"：

1. 质心法 (K-means) → 像在操场上找几个小组长（质心），然后让同学靠近最近的组长。

2. 密度法 (DBSCAN) → 像看人群聚集度，哪里人多就算一群，零散的人算"离群点"。

3. 分布法 (GMM) → 假设大家都按某种分布散开（比如正态分布），模型推测出每个分布。

4. 层次法 (Hierarchical) → 先大家都分开，逐渐合并成大类，就像画族谱一样。

---

所以，这里重点强调：

• K-means 因为 效率高、能扩展到大数据，所以最常用。

• 其他方法在某些特殊场景下更合适（比如 DBSCAN 在做异常检测时很强）。

---

三、K-means 聚类 (k-means clustering)

K-means 是一种非常流行的聚类算法，用于在 无监督学习 中对样本分组。它的基本步骤如下：

1. 迭代寻找最佳的 k 个中心点（质心 centroids）。

2. 把每个样本分配到最近的质心。同一个质心最近的样本，就属于同一个簇。

3. 算法会选择质心的位置，使得：

   • 每个点到最近质心的距离平方和最小（即最小化 SSE，Sum of Squared Errors）。

---

3-1、举例：狗的身高和宽度

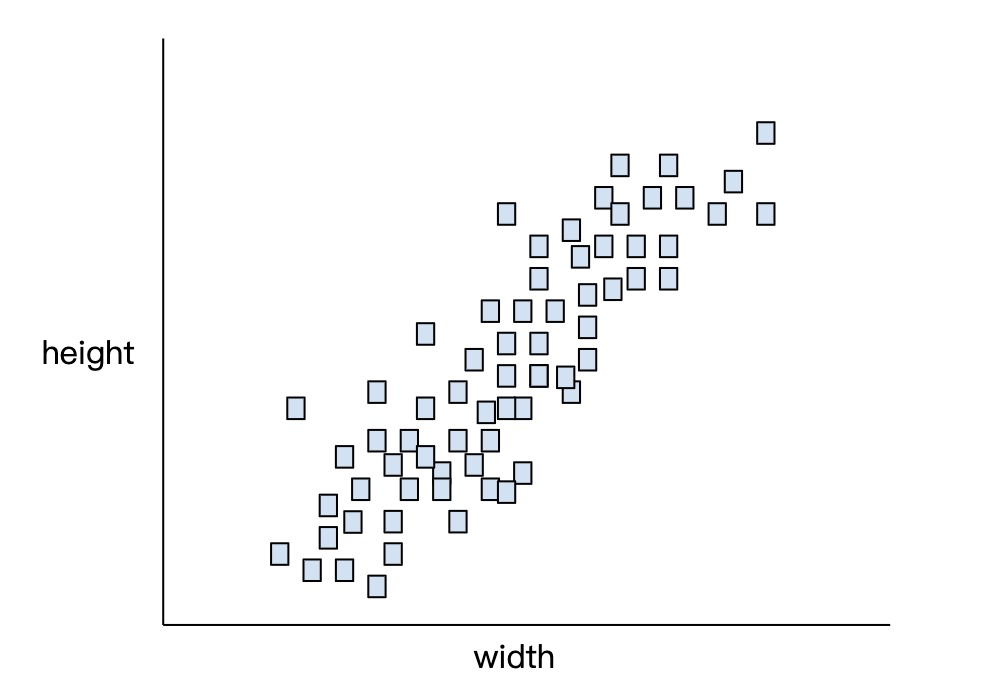
假设我们有一堆狗的数据：身高（height） 和 宽度（width），画在直角坐标图上。

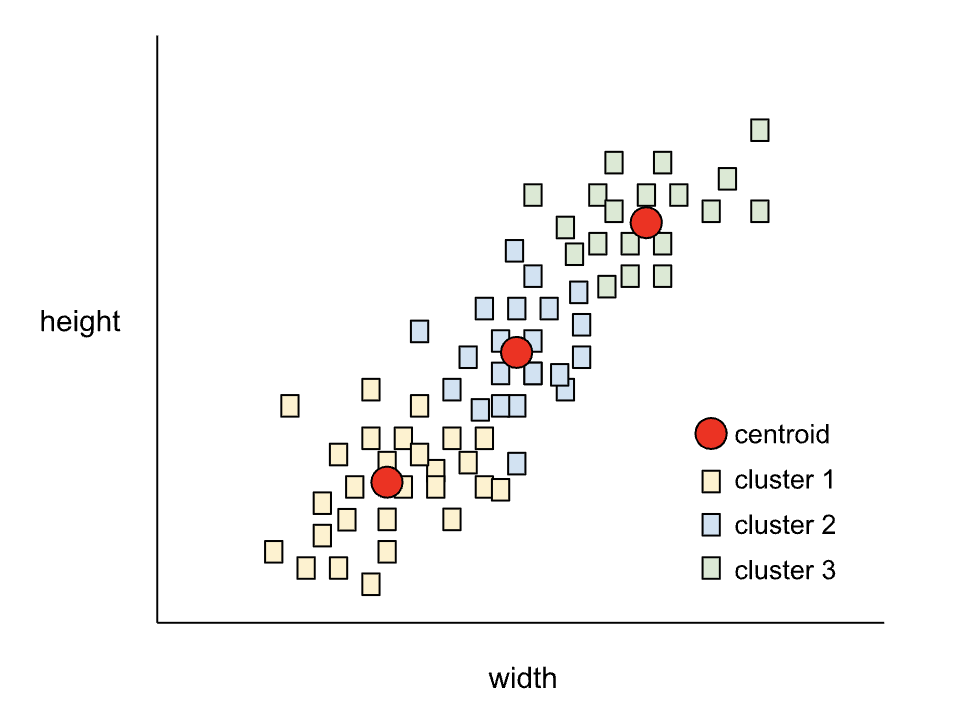
• 如果设定 k=3，那么 k-means 会生成三个质心。

• 每只狗会分配给最近的质心 → 得到三个簇。

• 原始散点图（狗的身高 vs 宽度）。

• 算法自动找到三个质心，把狗分为三组。

---

3-2、应用场景

比如，一个厂家想要确定 小号 / 中号 / 大号狗毛衣 的尺寸：

• 三个质心的坐标 = 每组狗的平均身高和平均宽度。

• 厂家就可以把这三个质心作为三种毛衣的标准尺码。

⚠️ 注意：质心不一定是真实的样本，它只是一个数学上的"平均点"。

---

3-3、高维数据

• 上面的例子只有 两个特征（height, width），画图很直观。

• 实际上，k-means 可以处理 任意多特征（比如 100 个维度），只是我们没法画出来而已。

---

3-4、通俗讲解

你可以把 k-means 想成一个"分小组"的过程：

1. 先随便找几个组长（质心）。

2. 每个学生（样本）都靠近最近的组长。

3. 每次重新算组长（平均值），直到分组稳定下来。

结果：数据就被自动分成了 k 个簇。

---

总结：

• K-means = 找 k 个质心 + 最近距离原则分组。

• 本质目标：让每个点到所属质心的距离平方和最小。

• 应用广泛：市场细分、图像压缩、推荐系统、客户分群、甚至狗毛衣定尺。

---

3-5、演示 k=3 的 k-means 分组过程

举例：假设有 6 个点

二维坐标（身高, 体重）：

A(1,1), B(1.5,2), C(3,4),
D(5,7), E(3.5,5), F(4.5,5)

我们要用 k=2（为了计算简单，我先用 2 簇，你也能看懂流程，换 k=3 一样）。

---

Step 1: 随机初始化质心

假设随机选两个点作为初始质心：

• C1 = A(1,1)

• C2 = D(5,7)

---

Step 2: 分配样本到最近的质心

计算每个点到两个质心的欧氏距离：

公式：

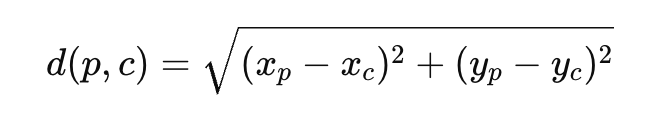
• 点 A(1,1)：

  • d(A,C1)=0 → 最近 C1

  • d(A,C2)=√[(1-5)²+(1-7)²] = √(16+36)=√52≈7.2

• 点 B(1.5,2)：

  • d(B,C1)=√[(1.5-1)²+(2-1)²]=√(0.25+1)=√1.25≈1.12 → C1

  • d(B,C2)=√[(1.5-5)²+(2-7)²]=√(12.25+25)=√37.25≈6.1

• 点 C(3,4)：

  • d(C,C1)=√[(3-1)²+(4-1)²]=√(4+9)=√13≈3.6 → C1

  • d(C,C2)=√[(3-5)²+(4-7)²]=√(4+9)=√13≈3.6 （正好一样，可以随便归一个，比如 C1）

• 点 D(5,7)：

  • d(D,C1)=√[(5-1)²+(7-1)²]=√(16+36)=√52≈7.2

  • d(D,C2)=0 → C2

• 点 E(3.5,5)：

  • d(E,C1)=√[(3.5-1)²+(5-1)²]=√(6.25+16)=√22.25≈4.72

  • d(E,C2)=√[(3.5-5)²+(5-7)²]=√(2.25+4)=√6.25=2.5 → C2

• 点 F(4.5,5)：

  • d(F,C1)=√[(4.5-1)²+(5-1)²]=√(12.25+16)=√28.25≈5.3

  • d(F,C2)=√[(4.5-5)²+(5-7)²]=√(0.25+4)=√4.25≈2.06 → C2

第一次分组结果：

• 簇1 (C1): A(1,1), B(1.5,2), C(3,4)

• 簇2 (C2): D(5,7), E(3.5,5), F(4.5,5)

---

Step 3: 更新质心

新的质心 = 每个簇点的均值（x̄, ȳ）。

• 新 C1 = 平均(A,B,C) = ((1+1.5+3)/3 , (1+2+4)/3) = (5.5/3 , 7/3) ≈ (1.83, 2.33)

• 新 C2 = 平均(D,E,F) = ((5+3.5+4.5)/3 , (7+5+5)/3) = (13/3 , 17/3) ≈ (4.33, 5.67)

---

Step 4: 重新分配

再计算每个点到新质心的距离，分组可能会变化。

重复 分配 → 更新质心，直到分组不再变化 = 收敛。

---

总结流程公式化