数据结构——二叉树学习

树

树是一种非线性的层级数据结构，它由节点（存储数据）和边（连接节点）组成，且结构中不存在循环路径。

这是自然中的树，看下面这个图片，大家看一下方便理解

在数据结构中，这个树的话就是就是到过来的自然的树，因为结构形状相似，这种结构叫做树

结点的度：⼀个结点含有子树的个数称为该结点的度；如上图：A的度为6
树的度：⼀棵树中，所有结点度的最⼤值称为树的度；如上图：树的度为6
叶子结点或终端结点：度为0的结点称为叶结点；如上图：B、C、H、I...等节点为叶结点
双亲结点或父结点：若⼀个结点含有子结点，则这个结点称为其子结点的父结点；如上图：A是B的父结点
孩子结点或子结点：⼀个结点含有的子树的根结点称为该结点的子结点；如上图：B是A的孩子结点
根结点：⼀棵树中，没有双亲结点的结点；如上图：A
结点的层次：从根开始定义起，根为第1层，根的⼦结点为第2层，以此类推
树的高度或深度：树中结点的最大层次；如上图：树的高度为4
树的以下概念只需了解，在看书时只要知道是什么意思即可：
⾮终端结点或分⽀结点：度不为0的结点；如上图：D、E、F、G...等节点为分⽀结点
兄弟结点：具有相同⽗结点的结点互称为兄弟结点；如上图：B、C是兄弟结点
堂兄弟结点：双亲在同⼀层的结点互为堂兄弟；如上图：H、I互为兄弟结点
结点的祖先：从根到该结点所经分⽀上的所有结点；如上图：A是所有结点的祖先
子孙：以某结点为根的⼦树中任⼀结点都称为该结点的⼦孙。如上图：所有结点都是A的子孙
森林：由m（m>=0）棵互不相交的树组成的集合称为森林

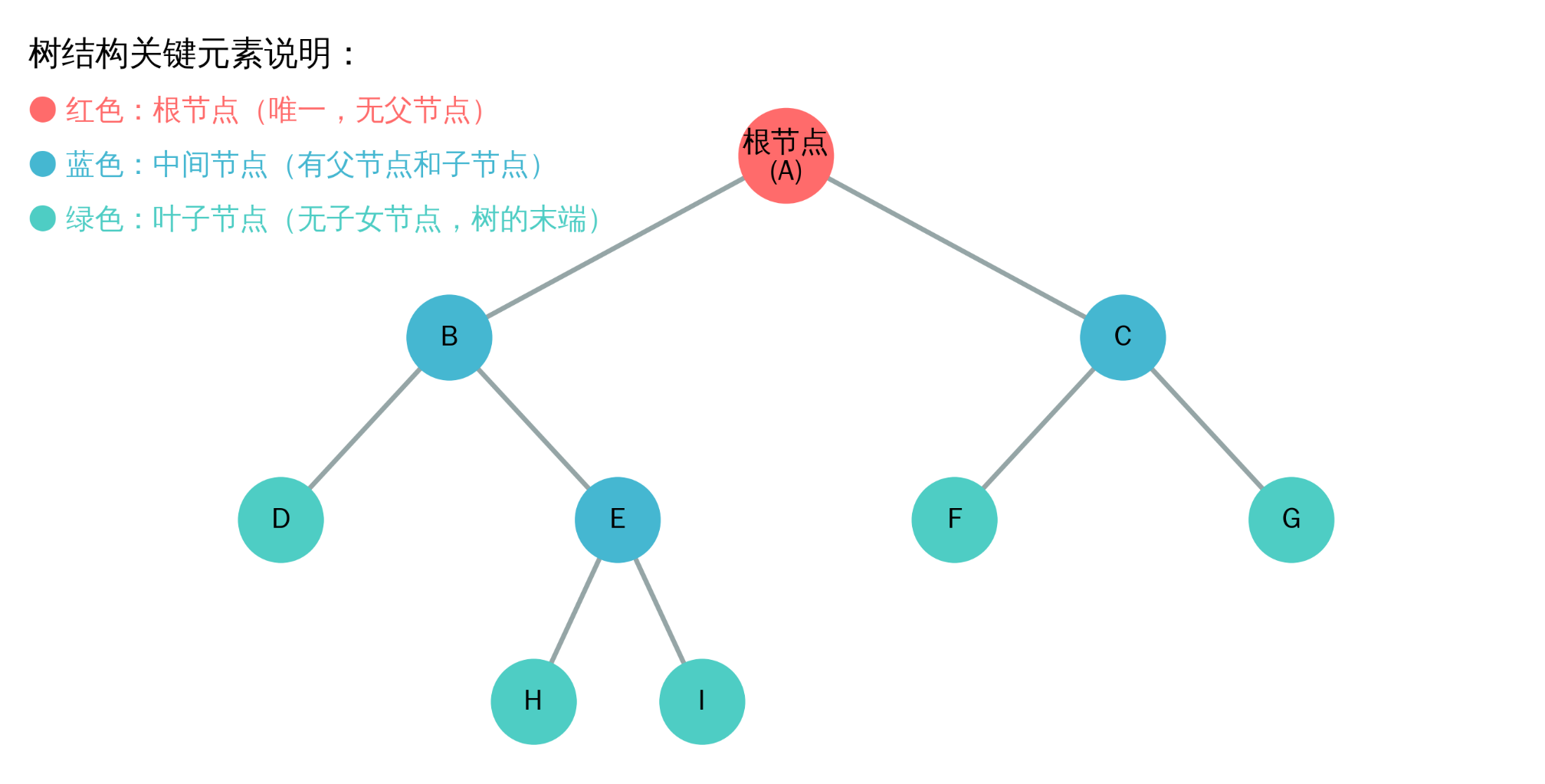
节点（Node）：树的基本构成单元，每个节点包含两部分 ------ 存储的数据本身，以及指向其子节点的引用（或指针）。
根节点 （Root）：树的起点，整个结构中唯一没有父节点的节点，所有其他节点都直接或间接从它衍生而来。
父子关系 ：若节点 A 直接连接到节点 B，则 A 是 B 的父节点，B 是 A 的子节点；一个父节点可以有多个子节点，但一个子节点只能有一个父节点。
层级（Level）：根节点位于第 1 层（部分定义中为第 0 层），其直接子节点位于第 2 层，以此类推，用于描述节点在树中的深度。
叶子节点 （Leaf）：没有任何子节点的节点，是树的 "末端" 节点。
无环特性：树的任意两个节点之间有且只有一条路径相连，整个结构中不存在循环（即不会出现 "节点 A→节点 B→节点 A" 的情况)。

树的关键特性

这些特性是树与其他数据结构（如链表、图）的核心区别：

非线性结构：数据不再像链表那样按顺序线性排列，而是以层级关系分布，能更自然地表示 "一对多" 的关联（如一个父节点对应多个子节点）。
唯一路径：任意两个节点之间仅存在一条连接路径，不存在多条路径或循环，保证了数据访问的唯一性。
n 个节点必有 n-1 条边：树的节点数和边数存在固定关系，n 个节点需要且仅需要 n-1 条边来连接，少一条则结构不连通，多一条则会出现循环。

二叉树的定义

二叉树是一种每个节点最多拥有两个子节点的树形数据结构，这两个子节点分别被称为左子节点和右子节点。也就是说其实二叉树是树的一个特殊的情况
⼀棵⼆叉树是结点的⼀个有限集合，该集合：

或者为空
或者是由⼀个根节点加上两棵别称为左子树和右子树的⼆叉树组成

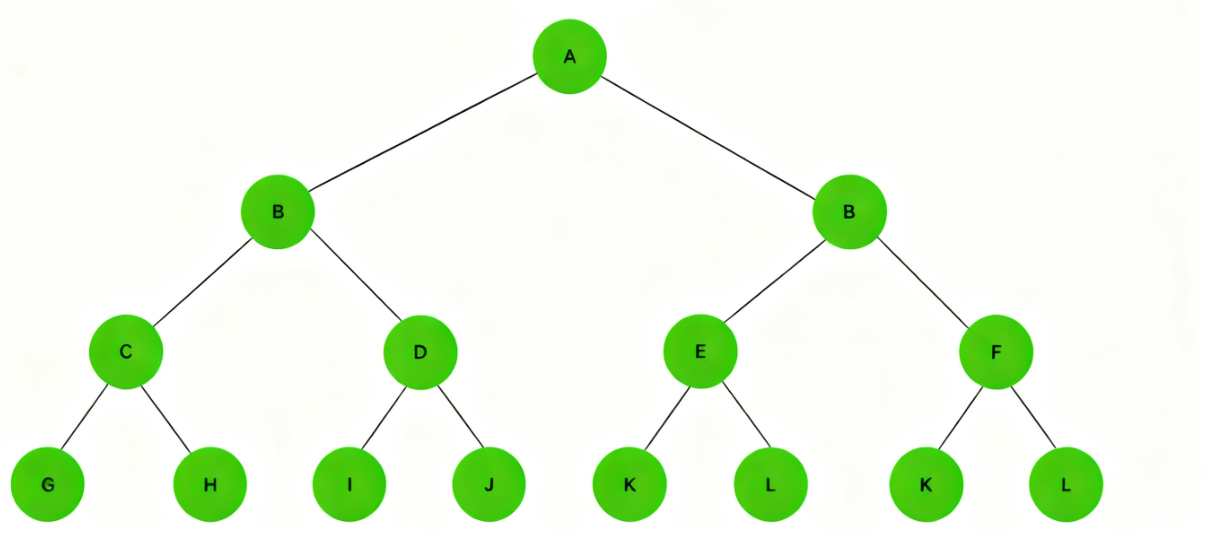
从上图可以看出：

⼆叉树不存在度⼤于2的结点
⼆叉树的子树有左右之分，次序不能颠倒，因此⼆叉树是有序树
注意：对于任意的二叉树都是由以下几种情况复合而成的

特殊的两种二叉树

1.满二叉树：一棵二叉树，如果每层的结点数都达到最大值，则这棵二叉树就是满二叉树。也就是说，如果一棵二叉树的层数为 K，且结点总数是 2的k次方−1，则它就是满二叉树。

2.完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为 K 的，有 n 个结点的二叉树，当且仅当其每一个结点都与深度为 K 的满二叉树中编号从 0 至 n-1 的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。

1.若规定根结点的层数为 1，则一棵非空二叉树的第 i 层上最多有 2的(i-1) 的次方个结点 (i>0)。

2.若规定只有根结点的二叉树的深度为 1，则深度为 K 的二叉树的最大结点数是 2的K次方 - 1 (k>=0)

3.对任何一棵二叉树，如果其叶结点个数为 n0，度为 2 的非叶结点个数为 n2，则有 n0 ＝ n2 ＋ 1。

4.具有 n 个结点的完全二叉树的深度 k 为 [log2 (n+1)]是向取整

5.对于具有 n 个结点的完全二叉树，如果按照从上至下、从左至右的顺序对所有节点从 0 开始编号，则对于序号为 i 的结点有：

若 i>0，双亲序号为：⌊(i−1)/2⌋；若 i=0，i 为根结点编号，无双亲结点。
若 2i+1 < n，左孩子序号为：2i+1，否则无左孩子。
若 2i+2 < n，右孩子序号为：2i+2，否则无右孩子。

6.二叉树的边数：在二叉树中，边的数量与节点的"度"密切相关：
度为0的节点(叶节点)：没有子节点，因此不贡献边
度为1的节点(叶节点)：有1个子节点，因此贡献1条边
度为2的节点(叶节点)：有1个子节点，因此贡献2条边

所以二叉树的总边数是 0 * n0 + 1 * n1 + 2 * n2 = n1 + 2 * n2

同时，二叉树与总结点的关系是总边数= N - 1,因为除了根节点外，每一个节点都由一条边"连接进来"，所以边数比总节点数 - 1
节点-1 =边数

java 复制代码

 1. 
某⼆叉树共有 399 个结点，其中有199 个度为 2 的结点，则该⼆叉树中的叶⼦结点数为（ ）
A 不存在这样的⼆叉树
B 200
C 198
D 199
//第一题叶子节点的n0 ＝ n2 ＋ 1。也就是说叶子节点是199，200个非叶子节点是对的
2.在具有2n 个结点的完全⼆叉树中，叶⼦结点个数为（）
A n
B n+1
C n-1
D n/2
//这个是偶数，因为由根节点的作用下，所以最后有一个父节点是单数的
//2n是总结点，这个是完整二叉树，n0是叶节点，n1是有一个子节点，n2是有两个子节点
//所以  n0 + n1 + n2 =  2n  分为三个不同的类型，每个类型加起来的结果就是总的节点
//让节点个数与边数式子联立
//节点-1 =边数
//   (n0 + n1 + n2) -1 =  n1 + 2 n2
3.⼀个具有767个节点的完全⼆叉树，其叶⼦节点个数为（）
A 383
B 384
C 385
D 386
//767   n + 2 n2 = 边数    n1 + 2 n2 + 1 = 节点
//n0 + n1 + n2 =  767   n2 + 1 - n0 = 0   
//n2  与 n0 的关系出来了带入一下就可以求出来了
//n1 + 2 n2 + 1 = 767带入到这里
4.⼀棵完全⼆叉树的节点数为531个，那么这棵树的⾼度为（ ）
A 11
B 10
C 8
D 12
//log2 (n+1)   
答案：
1.B
2.A
 3.B
 4.B

遍历二叉树

二叉树的遍历实现主要有以下几种方法，根据遍历顺序和实现方式可分为两大类别：

基于节点访问顺序（根节点、左子树、右子树的优先级），分为：

前序遍历（Pre-order）顺序：根节点 → 左子树 → 右子树示例：对于根为 A、左子树 B、右子树 C 的二叉树，遍历结果为 A → B → C（假设 B、C 为叶子节点）。
中序遍历（In-order）顺序：左子树 → 根节点 → 右子树示例：上述树的遍历结果为 B → A → C。注：对于二叉搜索树（BST），中序遍历结果为升序序列。
**后序遍历（Post-order）顺序：**左子树 → 右子树 → 根节点示例：上述树的遍历结果为 B → C → A。
层序遍历（Level-order）顺序 ：按层次（从根节点开始，逐层从左到右访问节点）示例：上述树的遍历结果为 A → B → C（若 B、C 在同一层）。
针对前、中、后序遍历，实现方式分为：
递归实现利用函数递归调用的栈特性，代码简洁直观，核心是递归处理左子树和右子树。示例

java 复制代码

def preorder(node):
    if node is None:
        return
    print(node.val)    # 访问根
    preorder(node.left)  # 左子树
    preorder(node.right) # 右子树

迭代实现手动使用栈模拟递归过程，适用于避免递归栈溢出或需要更高效率的场景。示例：

java 复制代码

def preorder_iterative(root):
    stack = [root]
    while stack:
        node = stack.pop()
        if node:
            print(node.val)
            stack.append(node.right)  # 右子树后入栈，先访问左子树
            stack.append(node.left)

层序遍历通常采用队列实现（迭代方式），依次将每层节点入队，出队时访问并将其左右子节点入队。
注意：如果题目给你一个前序或者后续 + 中序就可以把这个二叉树的结构写出来了。

前序和后续组合不可以画出这个二叉树

java 复制代码

 // 获取树中节点的个数
 
int size(Node root);
 // 获取叶⼦节点的个数
 
int getLeafNodeCount(Node root);
 C: DEFCBA      
D: ABCDEF
 // ⼦问题思路求叶⼦结点个数
 
// 获取第K层节点的个数
 
int getKLevelNodeCount(Node root,int k);
 // 获取⼆叉树的⾼度
 
int getHeight(Node root);
 // 检测值为value的元素是否存在
 
Node find(Node root, int val);
 //层序遍历
 
void levelOrder(Node root);
 // 判断⼀棵树是不是完全⼆叉树
 
boolean isCompleteTree(Node root)

1. 获取树中节点的个数（int size(Node root)）

思路：总节点数 = 根节点（1） + 左子树节点数 + 右子树节点数（递归拆分）。

java 复制代码

int size(Node root) {
    if (root == null) {
        return 0; // 空树节点数为0
    }
    // 根节点计数1，加上左右子树的节点数
    return 1 + size(root.left) + size(root.right);
}

2. 获取叶子节点的个数（int getLeafNodeCount(Node root)）

思路：叶子节点是 "左右子树都为空" 的节点。递归逻辑：

空树：0

根是叶子：1

否则：左子树叶子数 + 右子树叶子数

java 复制代码

int getLeafNodeCount(Node root) {
    if (root == null) {
        return 0;
    }
    // 左右子树都为空，当前节点是叶子
    if (root.left == null && root.right == null) {
        return 1;
    }
    // 否则递归计算左右子树的叶子数之和
    return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);
}

3. 获取第 K 层节点的个数（int getKLevelNodeCount(Node root, int k)）

思路：将 "求第 K 层节点数" 转化为 "求子树的第 K-1 层节点数"：

空树或 k<1：0

k=1：当前层只有根节点（1 个）

否则：左子树第 k-1 层节点数 + 右子树第 k-1 层节点数

java 复制代码

int getKLevelNodeCount(Node root, int k) {
    if (root == null || k < 1) {
        return 0;
    }
    if (k == 1) {
        return 1; // 第1层只有根节点
    }
    // 第k层节点数 = 左子树第k-1层 + 右子树第k-1层
    return getKLevelNodeCount(root.left, k-1) + getKLevelNodeCount(root.right, k-1);
}

4. 获取二叉树的高度（int getHeight(Node root)）

思路：树的高度 = 1 + 左右子树中较高的高度（递归到最底层）。

java 复制代码

int getHeight(Node root) {
    if (root == null) {
        return 0; // 空树高度为0
    }
    // 左子树高度
    int leftHeight = getHeight(root.left);
    // 右子树高度
    int rightHeight = getHeight(root.right);
    // 取左右最大高度 + 1（当前层）
    return Math.max(leftHeight, rightHeight) + 1;
}

检测值为 value 的元素是否存在（Node find(Node root, int val)）
思路：前序遍历查找（先查根，再查左子树，最后查右子树）。

java 复制代码

Node find(Node root, int val) {
    if (root == null) {
        return null; // 空树，未找到
    }
    if (root.val == val) {
        return root; // 找到，返回当前节点
    }
    // 左子树查找
    Node leftResult = find(root.left, val);
    if (leftResult != null) {
        return leftResult;
    }
    // 左子树未找到，查右子树
    return find(root.right, val);
}

6. 层序遍历（void levelOrder(Node root)）

思路：用队列实现（FIFO 特性），依次弹出当前层节点，同时将下一层节点入队。

java 复制代码

void levelOrder(Node root) {
    if (root == null) {
        return;
    }
    Queue<Node> queue = new LinkedList<>();
    queue.offer(root); // 根节点入队
    while (!queue.isEmpty()) {
        Node cur = queue.poll(); // 弹出当前层节点
        System.out.print(cur.val + " "); // 访问节点
        // 左子树不为空则入队
        if (cur.left != null) {
            queue.offer(cur.left);
        }
        // 右子树不为空则入队
        if (cur.right != null) {
            queue.offer(cur.right);
        }
    }
}

7. 判断一棵二叉树是不是完全二叉树（boolean isCompleteTree(Node root)）

思路：完全二叉树的层序遍历有特性：

若遇到一个节点左子树为空但右子树不为空 → 不是完全二叉树

若遇到一个节点左 / 右子树为空，后续所有节点必须是叶子节点（无左右子树）

java 复制代码

boolean isCompleteTree(Node root) {
    if (root == null) {
        return true; // 空树是完全二叉树
    }
    Queue<Node> queue = new LinkedList<>();
    queue.offer(root);
    boolean flag = false; // 标记是否进入"后续节点必须是叶子"的阶段
    while (!queue.isEmpty()) {
        Node cur = queue.poll();
        if (flag) {
            // 进入阶段后，当前节点必须无左右子树
            if (cur.left != null || cur.right != null) {
                return false;
            }
        } else {
            if (cur.left != null && cur.right != null) {
                // 左右子树都有，继续入队
                queue.offer(cur.left);
                queue.offer(cur.right);
            } else if (cur.left == null && cur.right != null) {
                // 左空右非空 → 不是完全二叉树
                return false;
            } else if (cur.left != null && cur.right == null) {
                // 左非空右空 → 进入阶段，后续节点必须是叶子
                queue.offer(cur.left);
                flag = true;
            } else {
                // 左右都空 → 进入阶段
                flag = true;
            }
        }
    }
    return true;
}