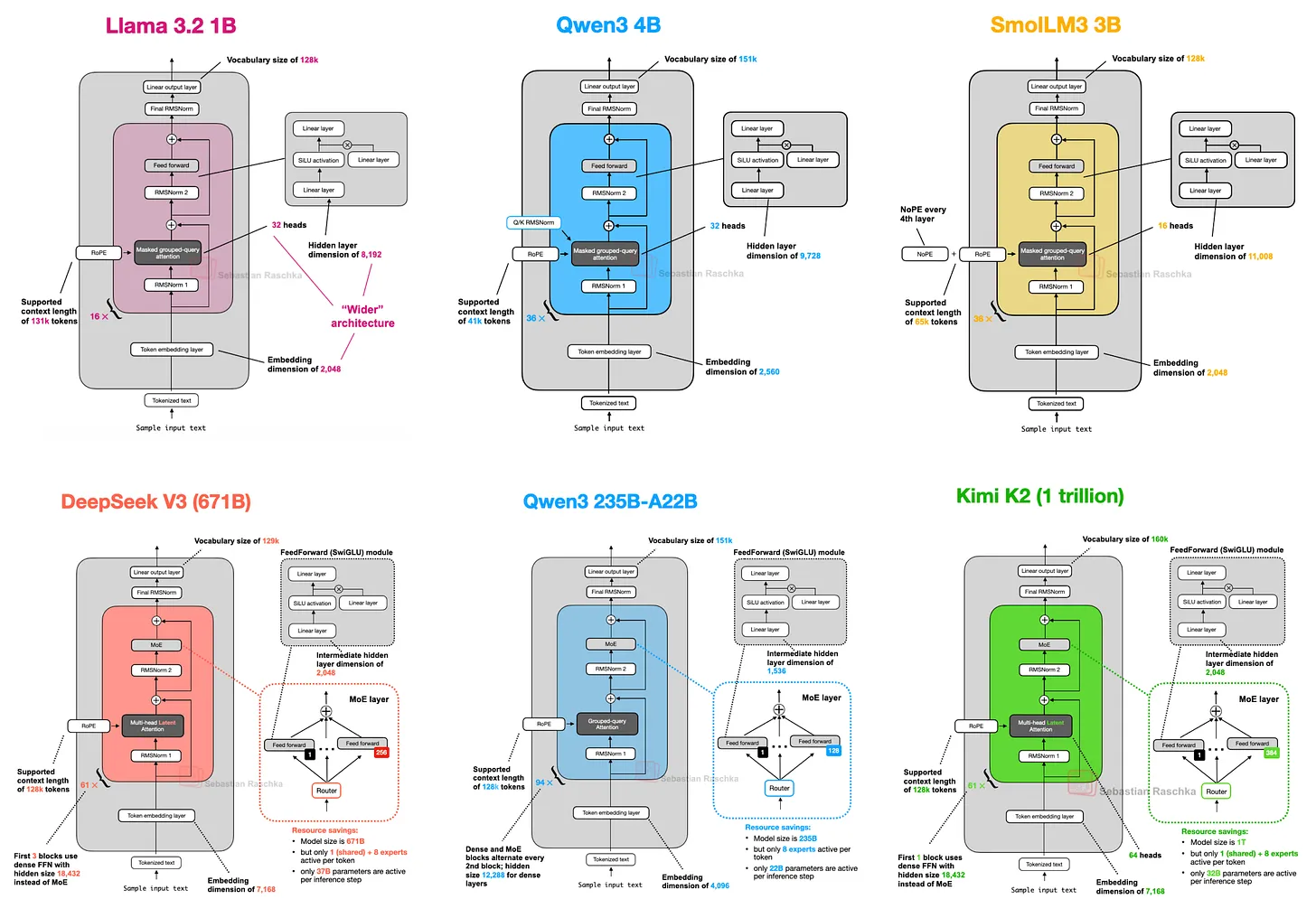
Part 6. Megatron Model Attention 注意力
本文大量依赖苏剑林老师的博文与文章下的评论,非常感谢!
GPT Model使用SelfAttention,是Attention基类的子类。linear层已经了解过。现在需要知道的是core attention和可选的qk norm。

在SelfAttention init时,初始化两个linear,两个norm和一个core attention。
- linear qkv一次性将hidden投影到query_projection_size + 2* KV_projection_size。query_projection_size = kv_channels * num_attention_heads,kv_projection_size = kv_channels * num_query_groups(GQA、MQA等)
- qknorm就是已经介绍过part 5中的layer norm。
有人认为QK norm会损害长距离建模性能,仅仅是用于稳定训练。Qwen3加入了2.5中没有的qk norm,deepseek没有。图源https://magazine.sebastianraschka.com/p/the-big-llm-architecture-comparison

- core attention默认使用DotProductAttention,标准缩放点积注意力计算。forward中,推理时支持开启KV缓存。具体流程:
- 前向Hidden->QKV(cache)->apply_rotary_pos_emb即QK RoPE->core_attention计算->output投影
- 反向允许重计算core attention,不保存中间激活。如果有dropout,要保证随机数生成器生成的掩码一样。之后就是QKV和输出的parallel linear来做模型张量并行。
RoPE embedding计算,只计算部分dim(t)的旋转,然后成对旋转,最后把旋转的部分和不旋转的(t_pass)拼起来返回。具体操作在embedding part介绍过。为什么可以把旋转和不旋转的部分拆开,旋转,再拼起来呢?因为两个点乘的QKV只要位置同时交换,不会影响最后求和的结果。(1,2,3)*(-1,-2,-3)T=(1,3,2)*(-1,-3,-2)T。不同的attention 有不同的旋转处理,具体要参考模型实现。freqs就是RotaryEmbedding返回的频率。


DotProductAttention中,会根据TP world size来划分头,不会进一步划分内部的内容。每个头维度d_k = kv_channels,每个TP有H_p = H/P个头,那么每个TP就有projection_size / P = H_p * P * kv_channels / P = H_p * kv_channels,即刚好是每个头的size乘以每个TP rank上有几个头。这里的计算其实有一点复杂也不太直观,可能是设计上的取舍。
前向传播的时候,输入的QKV是:np每个分区的头数,ng是每个分区有多少组,hn每个头的维度。于是输入就是[sq, b, ng, hn],序列在前,batch在后,最后是头数量和隐藏维度。sq是q序列的长度,sk就是key的,value和key保持对应。
- 首先,如果采用了分组,则在组内把KV重复多遍,匹配头的维度,体现在repeat_interleave这里。这样输入变成[sq, b, ng*head_per_group=np, hn]。
对不同的Query头,一部分头有着相同的KV值。例如32个头,32组Query投影形成32个Q,但是只有4个KV投影,把Q分成48,每8个Q都和相同的KV做计算,SOFTMAX( QK_g/sqrt(d_k) ) * V_g,下标g代表group,这样KV Cache可以大幅下降节约带宽)。为了匹配则需要把1,2,3,4扩展成11223344等。
- 然后把query塑造成[sq, b*np, hn],key也塑造成类似的样子。这样可以同时用一个巨大的矩阵乘法同时处理这一个batch中所有head的结果,而不是用缓慢的4D乘法
b, np, sq, sk\],即对这一个batch中,每个head,每一个sequence中的key对于q的分数。其实就是batch\*heads个方阵。
- 预先分配好矩阵运算结果buffer(预先创建torch.empty形状的tensor),接着调用torch.baddbmm,计算batch matrix-matrix product矩阵乘法,计算两个batch中矩阵的点乘。Batch Add Batch Matrix Multiply,output = beta * input + alpha * (batch1 @ batch2),这里beta就是0,alpha就是softmax scale即1/sqrt(d_k)。这一步得到了初步的attention scores,转换成[b, np, sq, sk]形状
- 进行mask,例如因果mask,屏蔽注意力矩阵的右上角,再添加softmax。然后得到dropout后的注意力(一般不这么干了)
- 再计算context(即value加权求和的内容):torch.bmm(scores, value),形状[b*np, sq, sk]x[b*np, sk, hn]=[b * np, sq, hn]->[b, np, sq, hn]
- 合并最后两个维度(每个分区的每个头拼接)得到[sq, b, np*hn],最终输出
离开core attention,乘以最后的linear proj,返回输出。
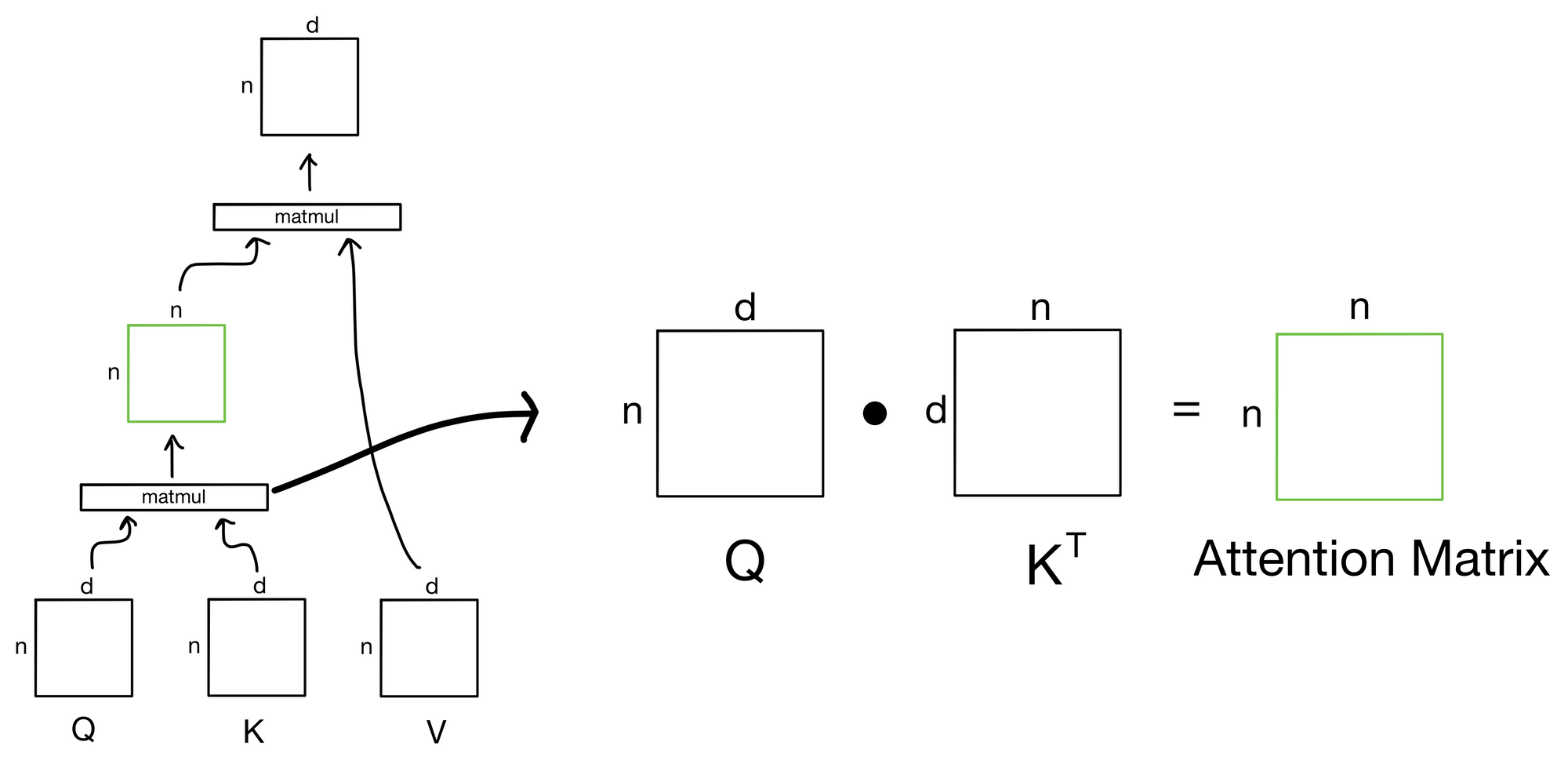
训练的时候需要对每个token都出logits,但是推理的时候只需要序列中最后一个。
上面就是最基本的Attention甚至是一个最普遍的transformer输出了。对于MLA这种比较特殊的attention,需要额外理解。
GQA可以看成一种低秩投影,把原本输入向量维度d,分别投影成k和v(d),然后又拆分给h个头(d/h),但是分成g个组,因此kv总维度变成了g * (d_k + d_v)=2gd/h。2g/h = 2的时候退化成MHA,但是h往往比g大很多,因此2g/h往往小于1,因此从输入d维度缩小成了比d更小的维度。为什么只考虑KV?因为核心的思路是查看GQA在KV缓存优化上的处理,已经用上了低秩投影的思路。MLA可以看成基于这个低秩投影的进一步改进、增强其表达方式。详见https://kexue.fm/archives/10091。MLA的KV cache维度变成了投影后的kv维度(比如512)而不再是强制性的2gd/h。
由于RoPE编码是用在QK计算之后的,在MLA中使用由于通过将QK矩阵合并计算 qk^T = xW_q R (c W_kR)T=x*W_q*R_{相对旋转}*W_kTc,RoPE在这里用上会导致中间三个矩阵WRW没法合并计算,因为R是变化的,所以计算不高效。如果把q也吸收进入c,并且把R放在c之后乘W之前,中间的Wq和Wk确实能合并,但是R和R之间就不能乘法,导致结果里没有显式的相对位置编码,只是把绝对的编码加进去,相对的模型要自己学,这其实就违背了RoPE的初衷。后来的做法是在每个attention head上的QK增加d_r维度,这几个维度仅仅用来添加RoPE,并且K增加的维度给所有Head共享。于是得到的kv cache是v原本的维度,再加上k原本维度加上新增的这个dr。于是总维度d_c+d_r,例如原论文的512+128/2=512+64.
最终版本MLA把Q输入也改成了低秩投影,只不过没有再投到KV共享的C里了,单独拿出来投到新的低秩里。这样或许可以进一步减少激活值(原论文说减小激活,是因为这部分能recompute)
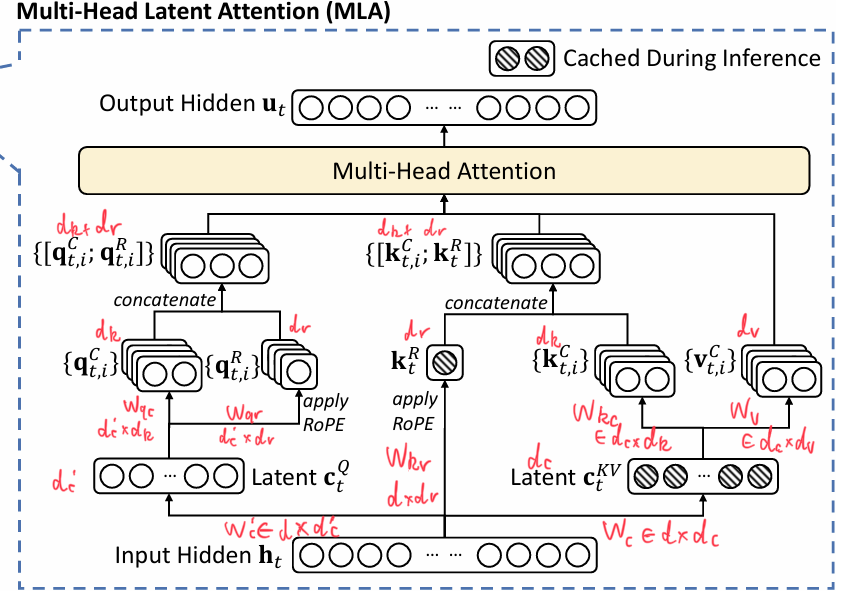

来自DeepSeek的论文,可以大概了解其结构。我把图中省略的矩阵以及维度都标注出来了。对每个token t的input hidden输入后分成三个部分:Q的潜在c{Q},KV共用的潜在c{KV},以及单独用来给K做旋转位置编码的K^r。潜在Q进一步升维度分成有RoPE的部分与没有RoPE的部分,拼接成最终Q(多个head);潜在KV中分成多头后,K拼接旋转编码的部分为最终K;于是最终Q和K与V就可以进入普通的MHA计算,最后作为新的output。注意,阴影部分为缓存的部分,只需要缓存潜在KV,以及K旋转位置编码部分。最终单个token的KV大小是d_c+d_r,相比GQA中(d_k+d_v)*g是要小很多的
为什么MLA可以在训练和推理两种模式中转化?
- 在进行训练的时候,MLA中独特的结构在于,添加了部分RoPE以及一些低秩投影矩阵。剩下的部分和MHA是完全一致的,相当于head size为d_k + d_r的MHA,因为MHA的关键点在于每个QKV都是不同且一一对应上的,在MLA训练中相当于也是把input投影成多个头然后每个头一一对应计算。
- 但是在推理的时候,MLA相当于一个MQA,因为MQA的要点是多个query对应同一组KV:
- 对于V来说,由于我们把KV压缩到了一个潜在向量中,在最后加权计算V的输出时得到output的操作可以放在最后,即上图中W_v的乘法放在output拼接前计算,于是相当于全程只有一个v潜在向量;
- 对于K来说,每个token的W_kc矩阵可以通过矩阵转置排序吸收到Q的计算里,于是K也是只有一个潜在向量;
- 对于Q来说,Q的计算变成从Q的潜在c_t^Q乘以潜在变换矩阵W_qc,再乘上K的潜在变换W_kc,拼接上RoPE。相当于Q有多少个head就有多少种,因为每个头都有自己的潜在变换矩阵
- 此时,Q和K的headsize为d_c+d_r,V的head size为d_c。按照原论文,这些size是普通设置情况下的4倍,所以增加了解码时期的计算量,降低了KV Cache
MLA通过把普通的复制操作替换为多个可学习的投影矩阵增加了原本GQA做不到的学习能力;同时又通过数学上的变换保障了推理时KV Cache的大小更小,保障了类似MQA的高效;另外,通过把显存的瓶颈(KV)转移到计算(更高的解码计算量)上缓解decode的真正瓶颈。
在prefill的时候,算力带宽显存都是瓶颈,直接用和训练一样的MHA形式计算。
一般的Attention中,heads * head size=hidden。MLA没有这个限制,因为其KV Cache大小和head size没有直接关系了(投影到latent中),因此deepseek V2中d_k=128,heads=128,乘起来为16384,是其隐藏维度hidden=5120的三倍。因此可以认为,虽然降低了KV,但是换一种方向上增加了总的attention dim