动机
好的模型需要对输入数据的扰动鲁棒性
- 使用有噪音的数据等价于Ti正则
- 丢弃法: 在层之间加入噪音
无偏差加入噪音
对x加入噪音得到x', 希望E[x′]=xE[x']=xE[x′]=x
丢弃法对每个元素进行如下操作
xi′={0with probablity pxi1−p otherise x_i^{'} = \begin{cases} 0 & with \ probablity \ p \\ \frac{x_i}{1-p} & \ otherise \end{cases} xi′={01−pxiwith probablity p otherise
其中xi1−p\frac{x_i}{1-p}1−pxi中1-p代表原始的概率,所以:
E[xi′]=p∗0+(1−p)xi′1−p=xi E[x_i^{'}] = p * 0 + (1-p)\frac{x_i^{'}}{1-p} \\ = x_i E[xi′]=p∗0+(1−p)1−pxi′=xi
如何使用丢弃法(Dropout)
丢弃法通常作用在隐藏全连接的输出上
h=σ(W1x+b1)h′=dropout(h)o=W2h′+b2y=softmax(o) h = \sigma(W_1x+b_1) \\ h' = dropout(h) \\ o = W_2h^{'} + b_2 \\ y = softmax(o) h=σ(W1x+b1)h′=dropout(h)o=W2h′+b2y=softmax(o)
其中hhh是第一个隐藏层的结果
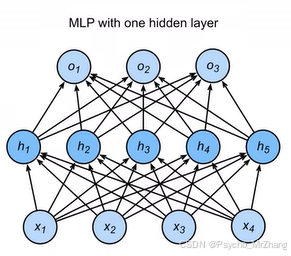
原始的网络结构
(模拟)加入Dropout的网路结构
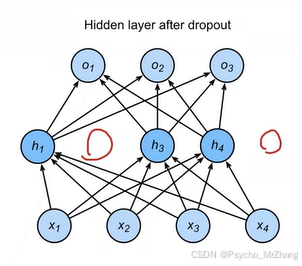
其中红色标记的位置是被随机为0的单元
丢弃法的作用范围
丢弃法只在训练中使用,添加正则项, 只影响参数的更新
推理过程中丢弃法
h=dropout(h)h = dropout(h)h=dropout(h)
输出的结果等于输入的结果