解码红黑树 - 技术栈

红黑树全面解析：从设计逻辑到代码落地

红黑树是自平衡二叉搜索树（Self-Balanced BST） 的经典实现，核心解决了普通 BST 失衡、AVL 树过度平衡的问题。它通过 "颜色约束" 实现 "大致平衡"，兼顾查找性能与插入 / 删除效率，成为 Linux 内核、Java TreeMap、C++ STL 等工业级组件的底层核心结构。本文将从 "为什么需要红黑树" 出发，逐步拆解定义、操作逻辑与代码实现，确保每个知识点清晰易懂。

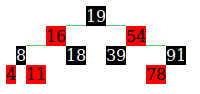
红黑树的设计背景：平衡与性能的折中

要理解红黑树，需先明确它与普通 BST、AVL 树的差异 ------ 红黑树的出现，本质是为了调和 "平衡" 与 "操作开销" 的矛盾。

三种树结构的核心对比

树结构	平衡规则	插入 / 删除调整开销	查找性能（最坏）	核心问题
普通 BST	无平衡约束	极低（无需调整）	O (n)（退化为链表）	数据有序插入时性能暴跌
AVL 树	严格平衡（左右子树高差≤1）	极高（频繁旋转 + 高度维护）	O(logn)	调整开销大，插入删除效率低
红黑树	大致平衡（最长路径≤2 倍最短路径）	中（少量旋转 + 颜色翻转）	O(logn)	兼顾平衡与操作效率，无明显短板

红黑树的设计初衷

AVL 树的 "严格平衡" 虽能保证最优查找性能，但每次插入 / 删除后需多次旋转、更新节点高度，操作开销过高；普通 BST 则完全无平衡约束，极端情况下性能退化。

红黑树的思路是：放弃 "绝对平衡"，用更宽松的约束实现 "大致平衡"------ 只要最长路径不超过最短路径的 2 倍，查找性能仍能稳定在 O (logn)，同时大幅减少插入 / 删除的调整次数。

红黑树的核心定义：5 条约束保证平衡

红黑树是满足以下 5 条颜色 + 结构规则的二叉搜索树（BST 的基础性质仍成立：左子树值＜根值＜右子树值）。这些规则共同确保 "大致平衡"。

5 条核心约束（必须牢记：左根右，根叶黑，不红红，黑路同）

颜色约束：每个节点只有两种颜色 ------ 红色（RED）或黑色（BLACK）；
根节点规则：树的根节点必须是黑色；
红节点相邻禁止：红色节点的父节点和子节点必须是黑色（即 "红不连红"）；
黑高相等规则 ：从任意节点出发，到其所有叶子节点（NIL 节点）的路径中，黑色节点的数量相等（这条路径的黑色节点数称为 "黑高"，记为bh）；
叶子节点规则：所有叶子节点（空节点，记为 NIL）视为黑色（代码中常用 "NIL 哨兵节点" 简化判断，避免空指针问题）。

关键推导：为什么约束能保证平衡？

假设某红黑树的黑高为bh（从根到 NIL 的黑色节点数）：

最短路径：全为黑色节点（无红色节点），长度 = 黑高bh；
最长路径：红黑相间（因 "红不连红"，红色节点最多与黑色节点数量相等），长度 = 2*bh；

由此可得：最长路径 ≤ 2 倍最短路径，树不会过度失衡，查找性能稳定在 O (logn)。

红黑树的节点设计：存储关键信息

红黑树的节点需支持 "追溯亲属关系" 和 "颜色判断"，因此在普通 BST 节点的基础上新增关键成员。但需注意：叔节点（Uncle）无需单独存储，可通过祖父节点动态推导（避免冗余）。

节点结构定义（C 语言）

c 复制代码

// 定义数据类型（可根据需求替换，如int、char等）
typedef int tn_datatype;

// 红黑树节点结构
typedef struct node {
    tn_datatype data;       // 节点存储的数据
    struct node *lchild;    // 左孩子指针
    struct node *rchild;    // 右孩子指针
    struct node *parent;    // 父节点指针（核心：用于追溯祖父/叔节点）
    int color;              // 颜色：0=BLACK（黑色），1=RED（红色）
} treenode, *linktree;

// 全局NIL哨兵节点（所有空叶子都指向它，避免重复创建空节点）
linktree NIL_NODE;

节点设计说明

parent：必须存在！红黑树的调整需要追溯父节点、祖父节点，普通 BST 无此成员，无法完成平衡修复；
color：新节点默认设为红色（关键原因：若设为黑色，会导致所有路径的黑高 + 1，需调整全树；设为红色仅可能违反 "红不连红"，调整范围极小）；
NIL_NODE：哨兵节点，颜色为黑色，所有空的左 / 右孩子都指向它，简化 "叶子节点判断"（比如无需检查lchild == NULL，直接判断lchild == NIL_NODE）。

辅助函数：推导祖父 / 叔节点

叔节点（Uncle）是父节点的兄弟，无需存储，通过祖父节点推导：

c 复制代码

// 获取节点的祖父节点（父节点的父节点）
linktree grandparent(linktree n) {
    if (n == NULL || n->parent == NULL) {
        return NULL;
    }
    return n->parent->parent;
}

// 获取节点的叔节点（父节点的兄弟）
linktree uncle(linktree n) {
    linktree g = grandparent(n);
    if (g == NULL) {
        return NULL; // 无祖父节点，则无叔节点
    }
    // 父节点是祖父的左孩子 → 叔节点是祖父的右孩子
    if (n->parent == g->lchild) {
        return g->rchild;
    } 
    else {
        return g->lchild;
    }
}

红黑树的插入操作：分场景修复平衡

插入流程遵循 "BST 插入 → 颜色修复" 两步：先按普通 BST 规则插入新节点（设为红色），再检查是否违反红黑约束，分场景修复。

插入前准备：BST 插入逻辑

先按 BST 规则找到新节点的插入位置，设置父节点，最后调用insertFixup修复平衡：

c 复制代码

// 按BST规则插入节点（返回插入后的根节点）
linktree bstInsert(linktree root, linktree newNode) {
    if (root == NIL_NODE) {
        return newNode; // 树空，新节点为根
    }
    linktree parent = NIL_NODE;
    linktree cur = root;
    // 找到插入位置（cur最终指向插入位置的父节点）
    while (cur != NIL_NODE) {
        parent = cur;
        if (newNode->data < cur->data) {
            cur = cur->lchild;
        } else if (newNode->data > cur->data) {
            cur = cur->rchild;
        } else {
            // 数据已存在（红黑树通常不允许重复值，可根据需求处理）
            free(newNode);
            return root;
        }
    }
    // 设置新节点的父节点，并入树
    newNode->parent = parent;
    if (newNode->data < parent->data) {
        parent->lchild = newNode;
    } else {
        parent->rchild = newNode;
    }
    // 初始化新节点的孩子为NIL（避免空指针）
    newNode->lchild = NIL_NODE;
    newNode->rchild = NIL_NODE;
    return root;
}

// 红黑树插入入口（对外接口）
void rbInsert(linktree *proot, tn_datatype data) {
    // 创建新节点，默认设为红色
    linktree newNode = (linktree)malloc(sizeof(treenode));
    newNode->data = data;
    newNode->color = 1; // 1=RED

    // 1. 按BST规则插入
    *proot = bstInsert(*proot, newNode);

    // 2. 修复红黑树约束
    insertFixup(proot, newNode);
}

插入后的平衡修复（insertFixup）

新节点为红色，可能违反的约束只有规则 3（红不连红）（其他规则均不涉及红色节点插入）。需根据 "父节点（P）的颜色" 和 "叔节点（U）的颜色" 分 3 种场景处理。

场景 1：父节点（P）是黑色 → 无违规，直接返回

若 P 为黑色，即使新节点（N）是红色，也满足 "红不连红"，且 "黑高" 未变（红色节点不贡献黑高）。

代码逻辑：

c 复制代码

if (newNode->parent->color == 0) { // 0=BLACK
    return;
}

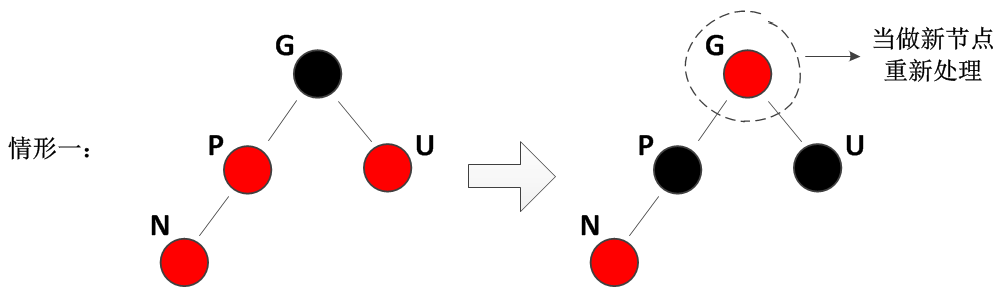
场景 2：父节点（P）是红色，且叔节点（U）是红色 → 颜色翻转 + 递归检查

违规原因：P 是红，N 是红 → 违反 "红不连红"；
修复思路：通过 "颜色翻转" 消除红节点相邻，同时保证黑高不变；
具体步骤：
- 将 P 和 U 的颜色改为黑色（消除 "红不连红"）；
- 将祖父节点（G）的颜色改为红色（保证黑高：原路径黑高 = G（黑）+P/U（黑），翻转后 = G（红）+P/U（黑），黑高不变）；
- 将 G 视为新的 "N"，递归检查（G 从黑变红，可能与 G 的父节点冲突）。

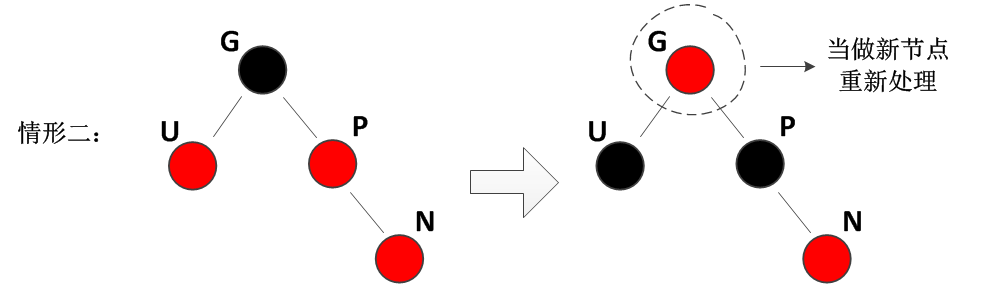
代码逻辑：

c 复制代码

linktree U = uncle(newNode);
linktree G = grandparent(newNode);

// 场景2：P红，U红
if (U != NIL_NODE && U->color == 1) { // 1=RED
    // 1. 翻转P、U为黑色
    newNode->parent->color = 0;
    U->color = 0;
    // 2. 翻转G为红色
    G->color = 1;
    // 3. 递归检查G
    insertFixup(proot, G);
}

场景 3：父节点（P）是红色，且叔节点（U）是黑色 → 旋转 + 颜色翻转

U 为黑色时，颜色翻转无法解决问题（翻转 G 为红后，G 与 P 仍红连红），需通过旋转调整节点位置，再翻转颜色。此场景需进一步按 "N、P、G 是否在一条直线" 细分（左右对称，以 "P 是 G 的左孩子" 为例）。

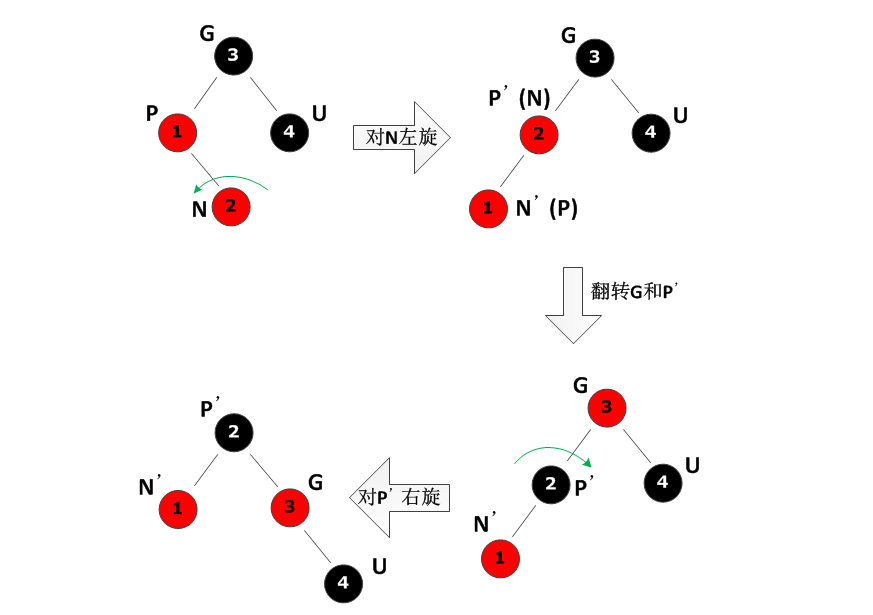
子场景 3.1：N、P、G 不在一条直线（N 是 P 的右孩子，P 是 G 的左孩子）

问题：N 在 P 的右子树，P 在 G 的左子树 → 三者呈 "折线"，无法直接旋转 G；
修复步骤 ：对 P 进行左旋转，将 N 转到 P 的父节点位置，使 N、P、G 呈 "直线"，再进入子场景 3.2。

左旋转函数（rbRotateLeft）：

c 复制代码

// 左旋转：将x的右孩子y转到x的位置，x成为y的左孩子
void rbRotateLeft(linktree *proot, linktree x) {
    linktree y = x->rchild; // y是x的右孩子
    x->rchild = y->lchild;  // y的左孩子转为x的右孩子

    if (y->lchild != NIL_NODE) {
        y->lchild->parent = x; // 更新y左孩子的父节点为x
    }

    y->parent = x->parent; // y的父节点继承x的父节点
    if (x->parent == NIL_NODE) {
        *proot = y; // x是根，则y成为新根
    } else if (x == x->parent->lchild) {
        x->parent->lchild = y; // x是左孩子，则y成为左孩子
    } else {
        x->parent->rchild = y; // x是右孩子，则y成为右孩子
    }

    y->lchild = x; // x成为y的左孩子
    x->parent = y; // x的父节点设为y
}

代码逻辑（子场景 3.1）：

c 复制代码

// N是P的右孩子，P是G的左孩子 → 左旋转P
if (newNode == newNode->parent->rchild && newNode->parent == G->lchild) {
    rbRotateLeft(proot, newNode->parent);
    newNode = newNode->parent; // 旋转后，原P成为新N的左孩子，更新N为原P
}

子场景 3.2：N、P、G 在一条直线（N 是 P 的左孩子，P 是 G 的左孩子）

修复步骤 ：
1. 将 P 的颜色改为黑色，G 的颜色改为红色（消除 "红不连红"）；
2. 对 G 进行右旋转（保证黑高不变，旋转后子树的黑节点数不改变）。

右旋转函数（rbRotateRight）：与左旋转对称，将 x 的左孩子 y 转到 x 的位置，x 成为 y 的右孩子。

c 复制代码

void rbRotateRight(linktree *proot, linktree x) {
    linktree y = x->lchild; // y是x的左孩子
    x->lchild = y->rchild;  // y的右孩子转为x的左孩子

    if (y->rchild != NIL_NODE) {
        y->rchild->parent = x;
    }

    y->parent = x->parent;
    if (x->parent == NIL_NODE) {
        *proot = y;
    } else if (x == x->parent->rchild) {
        x->parent->rchild = y;
    } else {
        x->parent->lchild = y;
    }

    y->rchild = x;
    x->parent = y;
}

代码逻辑（子场景 3.2）：

c 复制代码

// N是P的左孩子，P是G的左孩子 → 颜色翻转+右旋转G
newNode->parent->color = 0; // P改为黑色
G->color = 1;               // G改为红色
rbRotateRight(proot, G);    // 右旋转G

红黑树的删除操作：解决 "黑高缺失" 问题

删除是红黑树最复杂的操作，核心原因是：删除黑色节点会导致 "黑高减少"，违反规则 4（黑高相等） 。删除流程遵循 "BST 删除（转化为单孩子节点删除）→ 颜色修复"，先将复杂删除转化为简单场景，再分情况修复。

前置逻辑：将删除转化为 "单孩子节点删除"

若被删除节点（Old）有两个非空孩子，按 BST 规则：

用 Old 的前驱节点 （左子树最大值，无右孩子）或后继节点（右子树最小值，无左孩子）替代 Old 的数据；
问题转化为删除 "前驱 / 后继节点"（该节点最多只有一个孩子，记为 New）。

代码逻辑（找到前驱 / 后继）：

c 复制代码

// 找到节点的前驱（左子树最大值，无右孩子）
linktree getPredecessor(linktree node) {
    linktree cur = node->lchild;
    while (cur->rchild != NIL_NODE) {
        cur = cur->rchild;
    }
    return cur;
}

// 红黑树删除入口（对外接口）
void rbDelete(linktree *proot, tn_datatype data) {
    // 找到要删除的节点Old
    linktree Old = rbFind(*proot, data);
    if (Old == NIL_NODE) {
        printf("数据%d不存在\n", data);
        return;
    }

    // 转化为删除"最多一个孩子的节点"
    linktree delNode = Old; // 最终要删除的节点（前驱/后继）
    if (Old->lchild != NIL_NODE && Old->rchild != NIL_NODE) {
        // Old有两个孩子 → 用前驱替代
        delNode = getPredecessor(Old);
        Old->data = delNode->data; // 复制数据
    }

    // 执行删除并修复平衡（delNode最多一个孩子New）
    linktree New = (delNode->lchild != NIL_NODE) ? delNode->lchild : delNode->rchild;
    New->parent = delNode->parent; // 连接New和delNode的父节点

    if (delNode->parent == NIL_NODE) {
        *proot = New; // delNode是根，New成为新根
    } 
    else if (delNode == delNode->parent->lchild) {
        delNode->parent->lchild = New;
    } 
    else {
        delNode->parent->rchild = New;
    }

    // 若删除的是黑色节点，需修复黑高
    if (delNode->color == 0) { // 0=BLACK
        deleteFixup(proot, New);
    }

    free(delNode); // 释放删除节点的内存
}

// 辅助函数：查找节点（BST逻辑）
linktree rbFind(linktree root, tn_datatype data) {
    linktree cur = root;
    while (cur != NIL_NODE && cur->data != data) {
        if (data < cur->data) {
            cur = cur->lchild;
        } 
        else {
            cur = cur->rchild;
        }
    }
    return cur;
}

删除后的平衡修复（deleteFixup）

只有当删除的是黑色节点（delNode） 时，才需要修复（红色节点删除不影响黑高）。此时需根据 "New 的颜色" 和 "New 的兄弟节点（S）的颜色" 分场景处理。

核心问题："双黑" 标记

若 delNode 是黑色、New 也是黑色，删除后 New 所在路径的黑高减少 1------ 相当于 New "携带了一个额外的黑标记"，称为 "双黑"（New 本身是黑，加上缺失的 1 个黑，共 2 个黑）。修复的核心是 "消除双黑标记"。

场景 1：New 是红色 → 简单修复

修复思路：将 New 的颜色改为黑色，补充缺失的黑高；

代码逻辑：

c 复制代码

if (New->color == 1) { // 1=RED
    New->color = 0; // 改为黑色，补充黑高
    return;
}

场景 2：New 是黑色，兄弟节点（S）是红色 → 旋转 + 颜色翻转，转化为 S 为黑色的场景

修复思路：通过旋转将 S 的黑色子节点转为 New 的新兄弟，再按 S 为黑色的场景处理；
具体步骤：
- 将 S 的颜色改为黑色，New 的父节点（P）改为红色；
- 对 P 进行旋转（New 在左则左旋转，New 在右则右旋转）；
- 更新 S 为 New 的新兄弟（原 S 的子节点，颜色为黑色）。

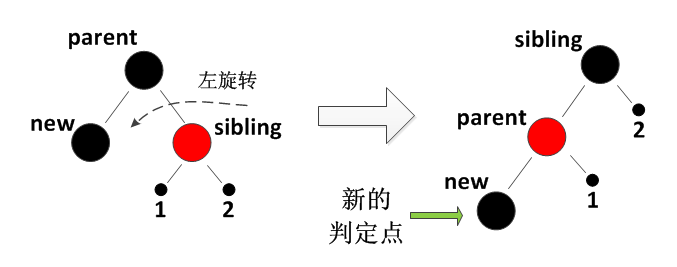
代码逻辑：

c 复制代码

linktree P = New->parent;
linktree S = (New == P->lchild) ? P->rchild : P->lchild; // S是New的兄弟

// 场景2：S是红色
if (S->color == 1) {
    S->color = 0;   // S改为黑色
    P->color = 1;   // P改为红色
    if (New == P->lchild) {
        rbRotateLeft(proot, P); // New在左，左旋转P
    } else {
        rbRotateRight(proot, P); // New在右，右旋转P
    }
    S = (New == P->lchild) ? P->rchild : P->lchild; // 更新S为新兄弟
}

场景 3：New 是黑色，兄弟节点（S）是黑色 → 按 S 的孩子（侄节点）颜色细分

S 为黑色时，需看 S 的两个侄节点（LN：S 的左孩子，RN：S 的右孩子）的颜色，分 3 种情况：

子场景 3.1：S 的两个侄节点（LN、RN）都是黑色 → 分摊双黑标记

修复思路：将 S 的颜色改为红色，把 "双黑标记" 转移给 P，递归检查 P；
逻辑：S 是黑色，LN、RN 也是黑色 → S 可贡献的黑高为 1，改为红色后，P 所在路径的黑高减少 1，相当于双黑标记转移到 P。

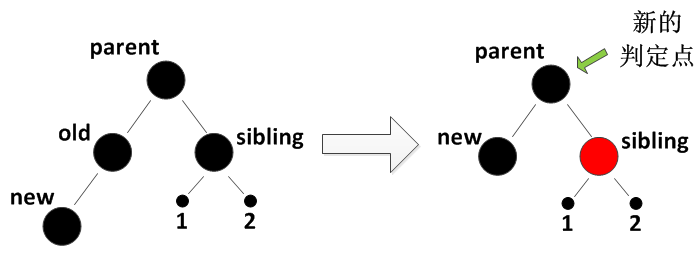
代码逻辑：

c 复制代码

if (S->lchild->color == 0 && S->rchild->color == 0) { // LN、RN都是黑色
    S->color = 1; // S改为红色
    New = P;      // 双黑标记转移到P
    P = New->parent;
    S = (New == P->lchild) ? P->rchild : P->lchild; // 更新S
}

子场景 3.2：S 的同边侄节点是红色（如 New 在左，LN 是红；New 在右，RN 是红）

修复思路：旋转 S → 旋转 P → 颜色翻转，消除双黑；
具体步骤（以 New 在左、LN 是红为例）：

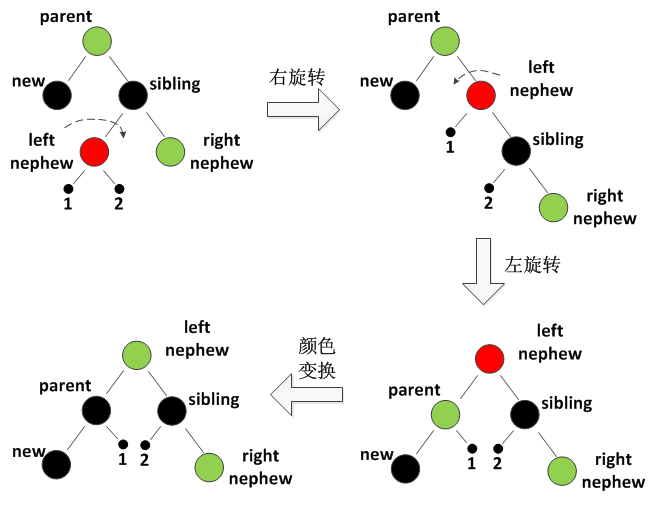
代码逻辑：

c 复制代码

// New在左，S的左侄（LN）是红色（同边）
if (New == P->lchild && S->lchild->color == 1) {
    rbRotateRight(proot, S); // 右旋转S
    S->color = S->parent->color; // 新S颜色继承原S的颜色
    S->parent->color = 1;        // 原S改为红色
    rbRotateLeft(proot, P);      // 左旋转P
    S->color = P->color;         // 新S颜色继承P的颜色
    P->color = 0;                // P改为黑色
}

子场景 3.3：S 的对边侄节点是红色（如 New 在左，RN 是红；New 在右，LN 是红）

修复思路：旋转 P → 颜色翻转，消除双黑；
具体步骤（以 New 在左、RN 是红为例）：

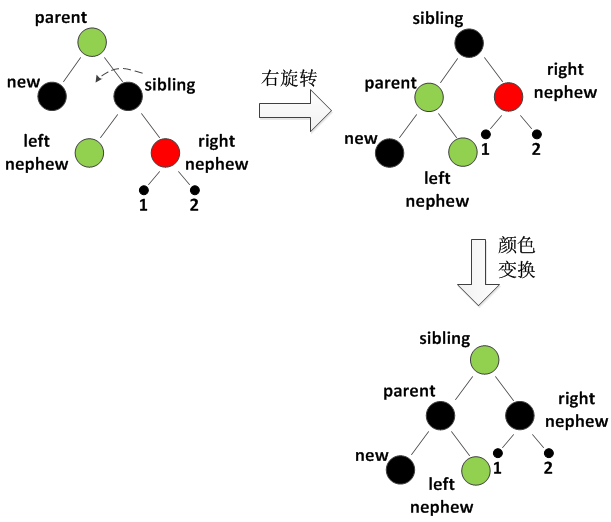
代码逻辑：

c 复制代码

// New在左，S的右侄（RN）是红色（对边）
if (New == P->lchild && S->rchild->color == 1) {
    rbRotateLeft(proot, P);  // 左旋转P
    S->color = P->color;     // S颜色继承P的颜色
    P->color = 0;            // P改为黑色
    S->rchild->color = 0;    // RN改为黑色
}