7.1 树的基本概念
1. 树的定义
树(Tree)是由 n (n≥0)n~(n\ge0)n (n≥0) 个结点组成的有限集合,记作 T。
- 如果 n=0n=0n=0 ,它是一颗空树;
- 如果 n>0n\gt0n>0 ,则为非空树,可以有图 7.1.1 所示的树的示例。
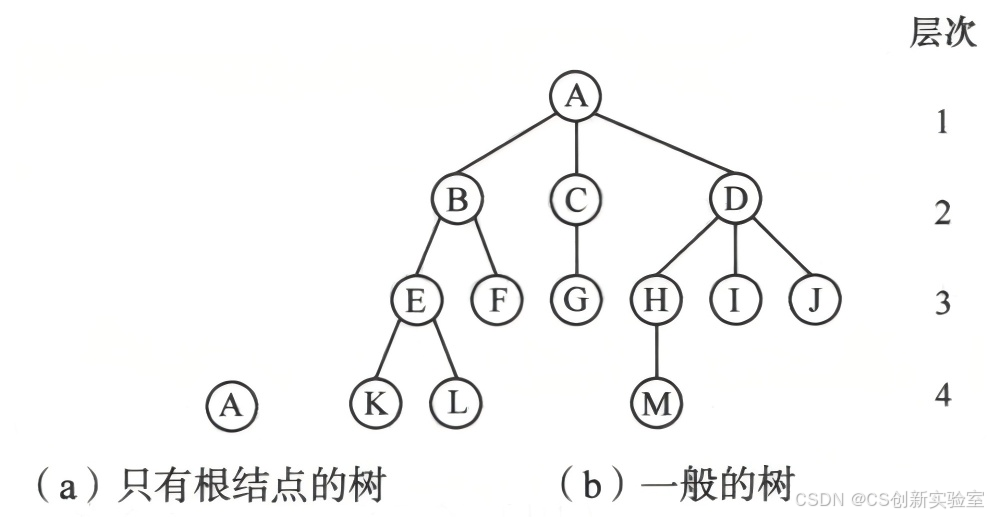
图 7.1.1 树的示例
对于非空树 T:
- 有且只有一个称为根结点(Root)的结点,简称根。
- 除根结点以外的其余结点可分为 m (m>0)m~(m\gt0)m (m>0) 个互不相交的有限集 T1,T2,⋯ ,TmT_1,T_2,\cdots,T_mT1,T2,⋯,Tm ,其中每一个集合本身又是一棵树,并且称为根的子树(Subtree)。
从以上可以看出,树的定义是递归的,因为在树的定义中又用到了树的定义。定义显示出了树固有的特性:一棵树由若干棵互不相交的子树构成,而子树又由更小的若干棵子树构成。
2. 树的逻辑表示
(1)以树形图表示:如图 7.1.1 所示,用一个圆圈表示一个结点,圆圈内的符号代表该结点的数据信息,结点之间的关系通过连线表示。虽然每条连线上都不带有箭头(即方向),但它仍然是有方向的,其方向隐含着从上向下,即连线的上方结点是下方结点的前驱结点,下方结点是上方结点的后继结点。它的直观形象是一棵倒置的树(树根在上,树叶在下)。
(2)以嵌套集合表示:如图 7.1.2 所示,每棵树对应一个圆圈,圆圈内包含根结点和子树的圆圈,同一个根结点下的各个子树对应的圆圈不能相交。结点之间的关系通过圆圈的包含来表示。
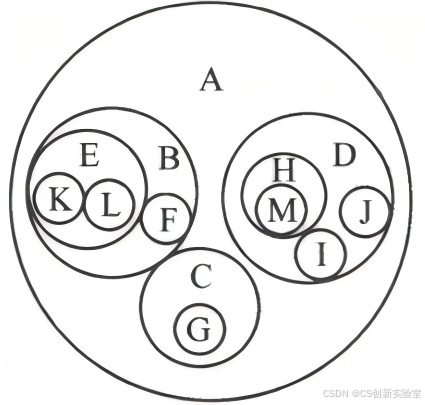
图 7.1.2 树的嵌套集合形式
(3)以广义表形式表示:如图 7.1.3 所示,根作为由子树组成的表的名字,写在表的左侧,形如 (root(T1,T2,...,Tm) 。每棵子树的表示方法与整棵树类似,各个子树之间用逗号分开。在这种形式中,结点之间的关系是通过括号的嵌套表示的。
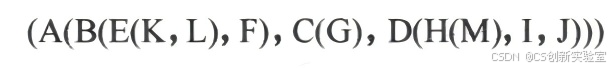
图 7.1.3 树的广义表形式
(4)以凹入形式表示:如图 7.1.4 所示,每棵树的根结点对应一条形,其子树的根对应着一个较短的条形,且树的根结点在上,子树的根在下,同一个根下各个子树的根对应的条形长度一样。
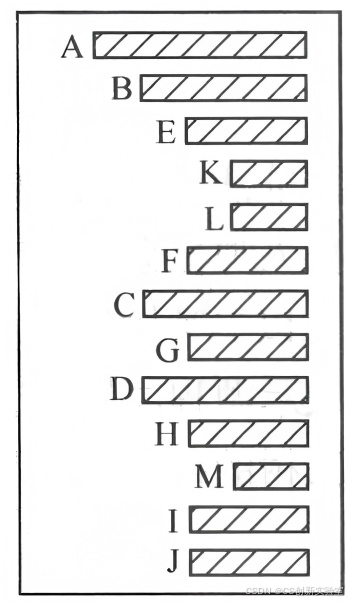
图 7.1.4 树的凹入形式
3. 树的基本术语
-
结点:树中的一个独立单元。包含一个数据元素及若干指向其子树的分支,如图 7.1.1(b) 中的 A、B、C、D 等。
-
结点的度:结点拥有的子树数称为结点的度。例如,图 7.1.1(b) 中结点 A 的度为 3,C 的度为 1,F 的度为 0。
-
树的度:树的度是树内各结点度的最大值。图 7.1.1(b) 所示的树的度为 3。通常将度为 mmm 的树称为 mmm 次树。
-
叶子:度为 0 的结点称为叶子或终端结点。图 7.1.1(b) 的结点 K、L、F、G、M、I、J 都是树的叶子。
-
非终端结点:度不为 0 的结点称为非终端结点或分支结点。除根结点之外,非终端结点也称为内部结点。
-
双亲和孩子:结点的子树的根称为该结点的孩子,相应地,该结点称为孩子的双亲。例如,图 7.1.1(b) 中 B 的双亲为 A,B 的孩子有 E 和 F。
-
兄弟:同一个双亲的孩子之间互称兄弟。例如,图 7.1.1(b) 的 H、I 和 J 互为兄弟。
-
祖先:从根到该结点所经分支上的所有结点。例如,图 7.1.1(b) 中 M 的祖先为 A、D 和 H。
-
子孙:以某结点为根的子树中的任一结点都称为该结点的子孙。如图 7.1.1(b) 中 B 的子孙为 E、K、L和 F。
-
层次:结点的层次从根开始定义起,根为第一层,根的孩子为第二层。树中任一结点的层次等于其双亲结点的层次加 1。
-
堂兄弟:双亲在同一层的结点互为堂兄弟。例如,图 7.1.1(b) 中结点 G 与 E、F、H、I、J 互为堂兄弟。
-
树的深度,或称为高度:树中结点的最大层次称为树的深度或高度。图 7.1.1(b) 所示的树的深度为 4。
注意:关于树的高度,不同资料会有不同约定,本书的约定,若只含有一个结点,树的高度为 1,空树的高度是 0。
-
有序树和无序树:如果将树中结点的各子树看成从左至右是有次序的(即不能互换),则称该树为有序树,否则称为无序树。在有序树中最左边的子树的根称为第一个孩子,最右边的称为最后一个孩子。
-
森林:是 m (m≥0)m~(m\ge0)m (m≥0) 棵互不相交的树的集合。对树中每个结点而言,其子树的集合即为森林。由此,也可以用森林和树相互递归的定义来描述树。
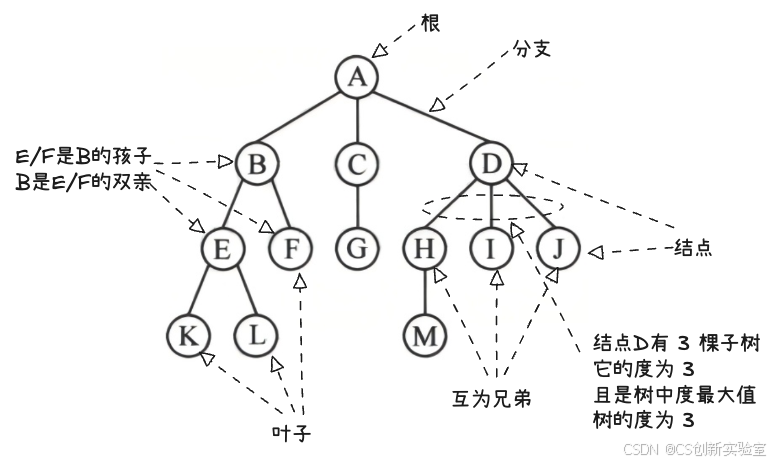
图 7.1.5 树的有关术语
就逻辑结构而言,任何一棵树都是一个二元组 Tree=(root,F) ,其中 root 是数据元素,称作树的根结点;F 是 m (m≥0)m~(m\ge0)m (m≥0) 棵树的森林,F=(T1,T2,⋯ ,Tm)\text{F}=(T_1,T_2,\cdots,T_m)F=(T1,T2,⋯,Tm) ,其中 Ti=(ri,Fi)T_i=(r_i,F_i)Ti=(ri,Fi) 称作根 root 的第 iii 棵子树;当 m≠0m\ne0m=0 时,在树根和其子树森林之间存在下列关系:
RF={<root,ri>∣i=1,2,⋯ ,m} RF=\{<root,r_i>|i=1,2,\cdots,m\} RF={<root,ri>∣i=1,2,⋯,m}
这个定义将有助于得到森林和树与二叉树之间转换的递归定义。