[算法设计与分析-从入门到入土] 查找&合并&排序&复杂度&平摊分析

个人导航

知乎：https://www.zhihu.com/people/byzh_rc

CSDN：https://blog.csdn.net/qq_54636039

注：本文仅对所述内容做了框架性引导，具体细节可查询其余相关资料or源码

参考文章：各方资料

文章目录

[[算法设计与分析-从入门到入土] 查找&合并&排序&复杂度&平摊分析](#[算法设计与分析-从入门到入土] 查找&合并&排序&复杂度&平摊分析)
个人导航
基础约定
[二分查找(binary search)](#二分查找(binary search))
[合并算法(merge two sorted lists)](#合并算法(merge two sorted lists))
[选择排序(selection sort)](#选择排序(selection sort))
[插入排序(insertion sort)](#插入排序(insertion sort))
[自底向上的合并(bottom-up merge sort)](#自底向上的合并(bottom-up merge sort))
复杂度分析
平均分析
[平摊分析(amortized analysis)](#平摊分析(amortized analysis))
- - - [经典场景 1：数组扩容](#经典场景 1：数组扩容)
    - [经典场景 2：双向链表的奇偶元素处理](#经典场景 2：双向链表的奇偶元素处理)
关键总结

基础约定

对数默认底数: log ⁡ n = log ⁡ 2 n \log n = \log_2 n logn=log2n
数组下标范围: 默认从 1 到 n
向下取整: ⌊ x ⌋ \lfloor x \rfloor ⌊x⌋
向上取整: ⌈ x ⌉ \lceil x \rceil ⌈x⌉
交换操作定义: 1 次交换 = 3 次赋值

x与y交换 -> temp=y, y=x, x=temp

二分查找(binary search)

若数组长度为 2n（偶数）：取第 n 个元素为中间值，左侧 n − 1 n-1 n−1 个元素，右侧 n 个元素
若数组长度为 2 n + 1 2n+1 2n+1（奇数）：取第 n 个元素为中间值，左右两侧各 n 个元素

合并算法(merge two sorted lists)

场景: 数组区间 [ p , q ] [p,q] [p,q] 和 [ q + 1 , r ] [q+1,r] [q+1,r] 已分别有序，需合并为 [ p , r ] [p,r] [p,r] 的有序数组

思路: 双指针法 + 额外开辟长度为 n 的辅助空间，排序后赋值回原数组

元素赋值次数：2n 次
比较次数： min ⁡ ( n 1 , n 2 ) ∼ ( n − 1 ) \min(n_1,n_2) \sim (n-1) min(n1,n2)∼(n−1) 次（ n 1 , n 2 n_1,n_2 n1,n2 为两个子数组长度）

选择排序(selection sort)

思路: 每一轮从未排序子序列中选择最小值，交换至已排序子序列的末尾

比较次数：固定为 n ( n − 1 ) 2 \frac{n(n-1)}{2} 2n(n−1) 次
元素赋值次数： 0 ∼ 3 ( n − 1 ) 0 \sim 3(n-1) 0∼3(n−1) 次（最优情况无需交换，最差情况需 n − 1 n-1 n−1 次交换）

插入排序(insertion sort)

思路: 将数组分为已排序（初始长度为 1）和未排序两部分，逐个将未排序元素插入已排序部分的合适位置

重点: 执行移动操作而非交换操作

比较次数： n − 1 ∼ n ( n − 1 ) 2 n-1 \sim \frac{n(n-1)}{2} n−1∼2n(n−1) 次（最优为数组已有序，最差为数组逆序）
元素赋值次数： 2 ( n − 1 ) ∼ 2 ( n − 1 ) + ∑ k = 1 n − 1 k 2(n-1) \sim 2(n-1)+\sum_{k=1}^{n-1}k 2(n−1)∼2(n−1)+∑k=1n−1k 次

自底向上的合并(bottom-up merge sort)

设A是一个包含n个元素的数组

首先，分成 ⌊ n / 2 ⌋ \lfloor n/2 \rfloor ⌊n/2⌋个长度为 2 的已排序序列
(若存在 1 个剩余元素，则将其传递到下一轮迭代)
其次，合并 ⌊ n / 4 ⌋ \lfloor n/4 \rfloor ⌊n/4⌋个连续的 "长度为 2 的序列" 对，得到 ⌊ n / 4 ⌋ \lfloor n/4 \rfloor ⌊n/4⌋个长度为 4 的已排序序列
(若剩余 3 个元素，则将其中 2 个元素与 1 个元素合并)
重复此过程

若当前的合并步长为 2 j − 1 2^{j-1} 2j−1, 待合并的剩余元素为 k 个:

若 1 ≤ k ≤ 2 j − 1 1 \le k \le 2^{j-1} 1≤k≤2j−1：剩余元素传递至下一轮合并
若 2 j − 1 < k < 2 j 2^{j-1} < k < 2^j 2j−1<k<2j：剩余元素需要在当前轮完成合并

轮次指标	比较次数 C j C_j Cj	赋值次数 A j A_j Aj
单轮计算	n 2 j ( 2 j − 1 ∼ 2 j − 1 ) \frac{n}{2^j}(2^{j-1} \sim 2^j-1) 2jn(2j−1∼2j−1)	n 2 j × 2 j + 1 = 2 n \frac{n}{2^j} \times 2^{j+1}=2n 2jn×2j+1=2n
总复杂度	n log ⁡ n 2 ≤ C ≤ n log ⁡ n − n + 1 \frac{n\log n}{2} \le C \le n\log n -n +1 2nlogn≤C≤nlogn−n+1	A = 2 n log ⁡ n A=2n\log n A=2nlogn

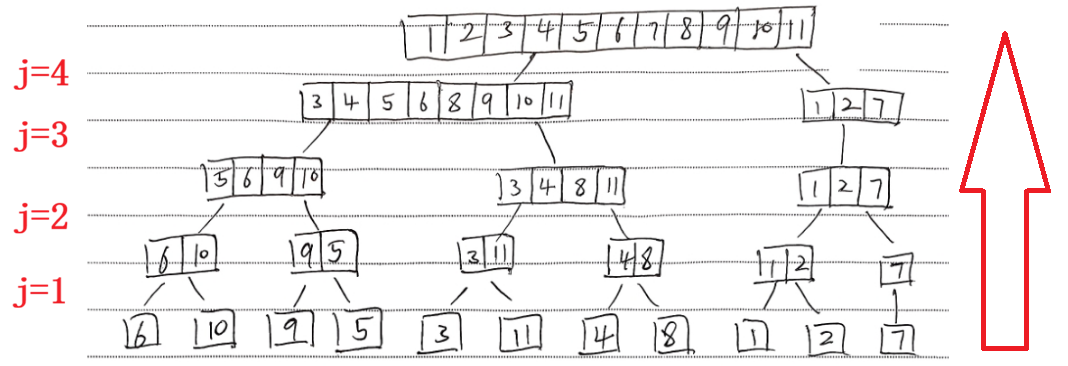
第一轮(j=1)是合并长度为1的子数组

-> k=1 -> 7传递到下一轮

第二轮(j=2)是合并长度为2的子数组

-> k=3 -> 12和7合并

第三轮(j=3)是合并长度为4的子数组

-> k=3 -> 127传到下一轮

第四轮(j=4)是合并长度为8的子数组

-> k=3 -> 合并all

复杂度分析

元运算：时间成本恒定的操作(与输入规模、算法无关)

时间复杂度 ：关注算法运行时间的增长率，而非具体运行时间

空间复杂度 ：算法运行所需的额外存储空间 ，不包含输入数据占用空间
空间复杂度上界 ≤ 时间复杂度 \text{空间复杂度上界} \leq \text{时间复杂度} 空间复杂度上界≤时间复杂度

复杂度量级分类

次线性: Sublinear
n c , n c log ⁡ k n , 0 < c < 1 n^c,~n^c\log^kn,~0<c<1 nc, nclogkn, 0<c<1
线性: Linear
c n cn cn
对数: Logarithmic
log ⁡ k n \log^kn logkn
次二次: Subquadratic
n 1.5 , n log ⁡ n n^{1.5}, n\log n n1.5,nlogn
二次: Quadratic
c n 2 cn^2 cn2
三次: Cubic
c n 3 cn^3 cn3

复杂度符号定义

符号	含义	数学定义	通俗解释
O ( g ( n ) ) O(g(n)) O(g(n))	上界（最坏情况）	∃ n 0 , c > 0 , ∀ n ≥ n 0 , f ( n ) ≤ c ⋅ g ( n ) \exists n_0,c>0, \forall n\ge n_0, f(n)\le c\cdot g(n) ∃n0,c>0,∀n≥n0,f(n)≤c⋅g(n)	运行时间不超过 g ( n ) g(n) g(n) 的常数倍
Ω ( g ( n ) ) \Omega(g(n)) Ω(g(n))	下界（最好情况）	∃ n 0 , c > 0 , ∀ n ≥ n 0 , f ( n ) ≥ c ⋅ g ( n ) \exists n_0,c>0, \forall n\ge n_0, f(n)\ge c\cdot g(n) ∃n0,c>0,∀n≥n0,f(n)≥c⋅g(n)	运行时间不低于 g ( n ) g(n) g(n) 的常数倍
Θ ( g ( n ) ) \Theta(g(n)) Θ(g(n))	精确界	∃ n 0 , c 1 , c 2 > 0 , ∀ n ≥ n 0 , c 1 g ( n ) ≤ f ( n ) ≤ c 2 g ( n ) \exists n_0,c_1,c_2>0, \forall n\ge n_0, c_1g(n)\le f(n)\le c_2g(n) ∃n0,c1,c2>0,∀n≥n0,c1g(n)≤f(n)≤c2g(n)	运行时间与 g ( n ) g(n) g(n) 同量级

性质:

f ( n ) = Ω ( g ( n ) ) ⟺ g ( n ) = O ( f ( n ) ) f(n)=\Omega(g(n)) \iff g(n)=O(f(n)) f(n)=Ω(g(n))⟺g(n)=O(f(n))
(若 f ( n ) f(n) f(n)是 g ( n ) g(n) g(n)的下界, 则 g ( n ) g(n) g(n)是 f ( n ) f(n) f(n)的上界)
f ( n ) = Θ ( g ( n ) ) ⟺ f ( n ) = O ( g ( n ) ) f(n)=\Theta(g(n)) \iff f(n)=O(g(n)) f(n)=Θ(g(n))⟺f(n)=O(g(n)) 且 f ( n ) = Ω ( g ( n ) ) f(n)=\Omega(g(n)) f(n)=Ω(g(n))
(若 f ( n ) f(n) f(n)是 g ( n ) g(n) g(n)的精确界, 则 f ( n ) f(n) f(n)即是 g ( n ) g(n) g(n)的上界, 又是 g ( n ) g(n) g(n)的下界)

典型函数复杂度

函数	O	Ω \Omega Ω	Θ \Theta Θ
任意常数函数	1	1	1
log ⁡ n k = k log ⁡ n \log n^k=k\log n lognk=klogn	log ⁡ n \log n logn	log ⁡ n \log n logn	log ⁡ n \log n logn
∑ j = 1 n log ⁡ j = log ⁡ n ! \sum_{j=1}^n\log j=\log n! ∑j=1nlogj=logn!	n log ⁡ n n\log n nlogn	n log ⁡ n n\log n nlogn	n log ⁡ n n\log n nlogn

log ⁡ n ! \log n! logn! 复杂度推导依据：利用积分近似面积

上界： ∑ j = 1 n log ⁡ j ≤ ∫ 1 n − 1 log ⁡ x d x + log ⁡ n = O ( n log ⁡ n ) \sum_{j=1}^n\log j \le \int_1^{n-1}\log x dx+\log n = O(n\log n) ∑j=1nlogj≤∫1n−1logxdx+logn=O(nlogn)

下界： ∑ j = 1 n log ⁡ j ≥ ∫ 1 n log ⁡ x d x = Ω ( n log ⁡ n ) \sum_{j=1}^n\log j \ge \int_1^{n}\log x dx = \Omega(n\log n) ∑j=1nlogj≥∫1nlogxdx=Ω(nlogn)

平均分析

前提: 需要已知输入数据的概率分布

以插入排序为例：(如果假设其是随机分布的话)

插入位置概率:
P i n s e r t = 1 i P_{insert}=\frac{1}{i} Pinsert=i1

单轮期望比较次数:
C i − e x p = i − 1 i + ∑ j = 1 i − 1 i − j i = i 2 − 1 i + 1 2 \begin{align} C_{i-exp}&= \frac{i-1}{i} + \sum_{j=1}^{i-1}\frac{i-j}{i} \\ &=\frac{i}{2} - \frac{1}{i} + \frac{1}{2} \end{align} Ci−exp=ii−1+j=1∑i−1ii−j=2i−i1+21

平均比较次数:
A v e r a g e C o m p a r i s o n = ∑ i = 2 n ( i 2 − 1 i + 1 2 ) = n 2 4 + 3 4 n − ∑ i = 1 n 1 n = Θ ( n 2 ) \begin{align} Average~Comparison &= \sum_{i=2}^{n}(\frac{i}{2} - \frac{1}{i} + \frac{1}{2}) \\ &= \frac{n^2}{4} + \frac{3}{4}n-\sum_{i=1}^{n}\frac{1}{n} \\ &=\Theta(n^2) \end{align} Average Comparison=i=2∑n(2i−i1+21)=4n2+43n−i=1∑nn1=Θ(n2)

平摊分析(amortized analysis)

情景: 算法中某操作的时间成本存在波动（偶尔耗时久，多数时间耗时短）

思想: 不依赖输入概率分布，将高成本操作的时间平摊至低成本操作上

经典场景 1：数组扩容

向数组中插入元素时，当数组已满，需要执行扩容操作

（通常扩容为原容量的 2 倍，需将原数组元素全部复制到新数组）

普通插入操作：时间复杂度为 O ( 1 ) O(1) O(1)（直接追加）
扩容时的插入操作：时间复杂度为 O ( n ) O(n) O(n)（复制 n 个元素）

平摊复杂度分析:

假设数组初始容量为 1，每次满容量时扩容为 2 倍，共执行 n 次插入

前 n 次插入中，扩容操作仅发生 log ⁡ n \log n logn 次（如插入第 2、4、8... 个元素时）
所有扩容操作 的总时间为 1 + 2 + 4 + ... + 2 ⌊ log ⁡ n ⌋ ≤ 2 n 1+2+4+...+2^{\lfloor \log n \rfloor} ≤ 2n 1+2+4+...+2⌊logn⌋≤2n
普通插入的总时间 = n − log ⁡ n < n n - \log n < n n−logn<n
将扩容的总时间平摊到所有插入操作 后，每个插入操作的平摊时间为 O ( n ) n = O ( 1 ) \frac{O(n)}{n}=O(1) nO(n)=O(1)

经典场景 2：双向链表的奇偶元素处理

初始双向链表仅含节点 "0"
输入数组 A [ 1 ... n ] A[1...n] A[1...n]，对每个元素x执行：
1. 若x是奇数：将x追加到链表末尾
2. 若x是偶数：先追加x，再删除x之前的所有奇数元素

e.g.示例演示（输入 A = [ 5 , 7 , 3 , 4 , 9 , 8 , 7 , 3 ] A=[5,7,3,4,9,8,7,3] A=[5,7,3,4,9,8,7,3]）

处理步骤：

5（奇）→ 链表：0→5

7（奇）→ 链表：0→5→7

3（奇）→ 链表：0→5→7→3

4（偶）→ 追加 4，删除之前的奇数（5、7、3）→ 链表：0→4

9（奇）→ 链表：0→4→9

8（偶）→ 追加 8，删除之前的奇数（9）→ 链表：0→4→8

7（奇）→ 链表：0→4→8→7

3（奇）→ 链表：0→4→8→7→3

平摊复杂度分析:

最坏情况单次操作 ：若连续插入奇数后插入偶数，删除操作需遍历所有奇数，单次时间复杂度为 O ( n ) O(n) O(n)，整体看似 O ( n 2 ) O(n^2) O(n2)
平摊分析核心 ：每个奇数元素仅会被删除一次（被删除后不会再出现在链表中）
总操作次数：
- 追加操作：共 n 次（每个元素都追加）
- 删除操作：最多 n 次（每个奇数仅被删一次）
总时间为 O ( n ) + O ( n ) = O ( n ) O(n)+O(n)=O(n) O(n)+O(n)=O(n)，平摊到 n 次操作后，整体复杂度为 Θ ( n ) \Theta(n) Θ(n)

关键总结

	C	A	O O O	Ω \Omega Ω	Θ \Theta Θ
选择排序Selection	n ( n − 1 ) 2 \frac{n(n-1)}{2} 2n(n−1)	0 ∼ 3 ( n − 1 ) 0\sim 3(n-1) 0∼3(n−1)	n 2 n^2 n2	n 2 n^2 n2	n 2 n^2 n2
插入排序Insertion	n − 1 ∼ n ( n − 1 ) 2 n-1 \sim \frac{n(n-1)}{2} n−1∼2n(n−1)	C + ( n − 1 ) C+(n-1) C+(n−1)	n 2 n^2 n2	n n n	n 2 n^2 n2
自底向上Bottom Up Merge	n log ⁡ n 2 ∼ n log ⁡ n − n + 1 \frac{n\log n}{2}\sim n\log n-n+1 2nlogn∼nlogn−n+1	2 n log ⁡ n 2n\log n 2nlogn	n log ⁡ n n\log n nlogn	n log ⁡ n n\log n nlogn	n log ⁡ n n\log n nlogn