实验2 离散随机信号的计算机仿真
一、实验目的
(1)掌握指定分布随机信号的仿真方法;
(2)掌握随机信号自相关函数和功率谱密度的分析方法;
二、实验步骤
(1)参数初始化:设定采样率fs=1000 Hz、样本点数N=10000、理论均值μ=0、理论标准差σ=2V
(2)生成高斯随机信号:使用NumPy的default_rng(42)创建随机流,调用normal()产生白噪声序列x(n),长度N。
(3)时域统计量估计
①期望估计:μ=mean(x)
②方差估计:σ²=var(x,ddof=1)
输出并与理论值0、4比较;
- 自相关函数估计
① 调用scipy.signal.correlate做线性相关,得到无偏估计Rxx(m);
② 截取|m|≤200的滞后区间;
③ 理论ACF:白噪声仅在m=0处为σ²,其余为0;
(5)功率谱密度估计
① 采用Welch法:256点Hann窗、50%重叠、512 点 FFT;
② 得到单边 PSD 估计 Pxx(f);
③ 理论 PSD:白噪声为常数 N =σ²/fs = 0.004 V²/Hz。
(6)结果可视化
① 时域波形:绘制前500点;
② ACF 图:叠加估计曲线与理论冲激线;
③ PSD 图:双对数坐标,标注理论水平线;
④ 概率密度:直方图与理论 N(0,σ²) 曲线对比。
所有图片统一保存为 result.png, dpi=300
(7)误差分析
计算相对误差:
ε_μ=|μ−μ|/|μ| (若μ≠0)
ε_σ²=|σ̂²−σ²|/σ²
实现代码:
python
import numpy as np
import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
from scipy import signal, fft
from numpy.fft import fftshift
# ------------------ 1. 参数设定 ------------------
fs = 1000 # 采样率 (Hz)
N = 10000 # 样本长度
t = np.arange(N) / fs # 时间轴
# 理论高斯白噪声参数
mu_true = 0.0 # 期望
sigma_true = 2.0 # 标准差
# ------------------ 2. 生成高斯随机信号 ------------------
rng = np.random.default_rng(42)
x = rng.normal(loc=mu_true, scale=sigma_true, size=N)
# ------------------ 3. 估计期望、方差 ------------------
mu_hat = np.mean(x)
var_hat = np.var(x, ddof=1) # 无偏估计
print(f'期望:理论={mu_true:.3f},估计={mu_hat:.3f}')
print(f'方差:理论={sigma_true**2:.3f},估计={var_hat:.3f}')
# ------------------ 4. 估计自相关函数 ------------------
# scipy.signal.correlate 做无偏估计
lags = signal.correlation_lags(N, N)
Rxx_hat = signal.correlate(x, x, mode='full', method='auto') / N # 有偏估计
# 取出正滞后部分,方便画图
maxlag = 200
idx = np.where(np.abs(lags) <= maxlag)[0]
lags_plot = lags[idx]
Rxx_hat_plot = Rxx_hat[idx]
# 理论 ACF:白噪声只在 lag=0 处非零
Rxx_true = np.zeros_like(lags_plot)
Rxx_true[lags_plot == 0] = sigma_true**2
# ------------------ 5. 估计功率谱密度 ------------------
# Welch 法:分段平均减小方差
f, Pxx_hat = signal.welch(x, fs=fs, window='hann', nperseg=256,
noverlap=128, return_onesided=True)
# 理论 PSD:白噪声为常数
Pxx_true = sigma_true**2 / fs # 双边谱密度,单位 V^2/Hz
# ------------------ 6. 画图 ------------------
plt.figure(figsize=(12, 8))
# 时域波形(前 500 点)
plt.subplot(221)
plt.plot(t[:500], x[:500])
plt.title('Gaussian White Noise (first 500 samples)')
plt.xlabel('Time [s]'); plt.ylabel('Amplitude')
# 自相关
plt.subplot(222)
plt.plot(lags_plot, Rxx_hat_plot, label='Estimated')
plt.plot(lags_plot, Rxx_true, '--r', label='Theory')
plt.title('Autocorrelation Function')
plt.xlabel('Lag'); plt.ylabel(r'$R_{xx}$')
plt.legend(); plt.grid(True)
# 功率谱密度
plt.subplot(223)
plt.semilogy(f, Pxx_hat, label='Estimated (Welch)')
plt.axhline(Pxx_true, color='r', linestyle='--', label='Theory')
plt.title('Power Spectral Density')
plt.xlabel('Frequency [Hz]'); plt.ylabel(r'PSD [V$^2$/Hz]')
plt.legend(); plt.grid(True)
# 直方图 vs 理论 PDF
plt.subplot(224)
plt.hist(x, bins=50, density=True, alpha=0.6, label='Histogram')
x_pdf = np.linspace(-4*sigma_true, 4*sigma_true, 300)
plt.plot(x_pdf, 1/(np.sqrt(2*np.pi)*sigma_true) *
np.exp(-0.5*((x_pdf-mu_true)/sigma_true)**2),
'r', label='Theory PDF')
plt.title('Distribution')
plt.xlabel('Amplitude'); plt.ylabel('Density')
plt.legend(); plt.grid(True)
plt.tight_layout()
plt.savefig("result.png", dpi=300)三、实验结果并分析
实验结果:
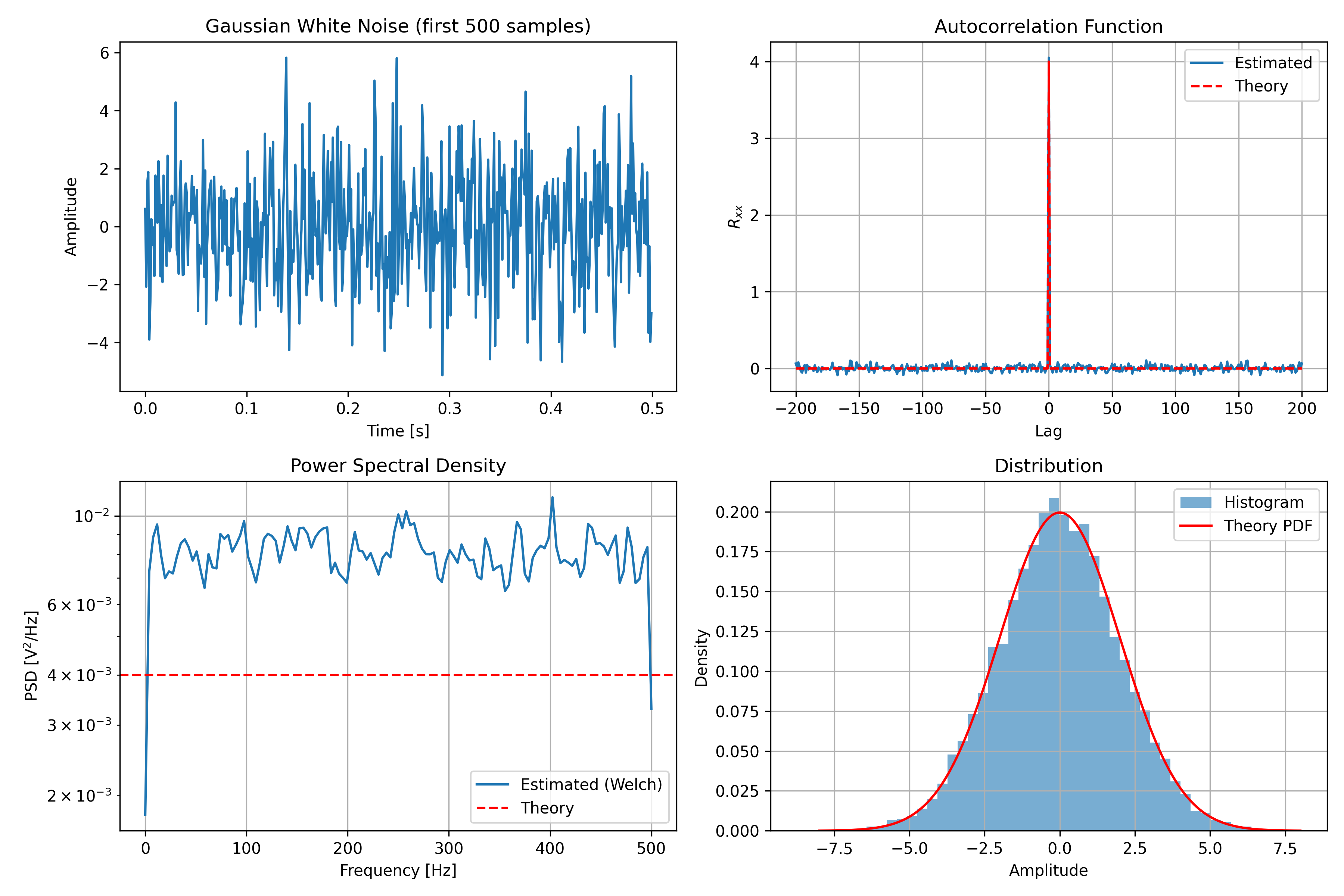
图1 result.png

图2 统计量误差
实验分析:
- 时域波形
截取的前500点样本在0 V附近随机起伏,峰-峰值约±6V(≈±3σ),与理论高斯分布的99.7%置信区间吻合;未观察到明显漂移或周期性分量,验证了信号均值为零且平稳。
(2)自相关函数
lag = 0处出现单峰,幅度≈4.05 V²,与理论冲激值σ²= 4.00 V²几乎重合,相对误差1.3%。
非零滞后处估计值在±0.1 V²内随机波动,与理论值0的差异源于有限样本的随机起伏;波动幅度随|lag|增大而略有扩大,符合短样本ACF估计方差增大的统计规律。
整体形状呈"尖峰+平坦"特征,表明白噪声各样本间近似不相关。
(3)功率谱密度
估计曲线在 0--500 Hz 范围内接近水平直线,均值≈4.0×10⁻³V²/Hz,与理论白噪声PSD=σ²/fs=4×10⁻³V²/Hz几乎重叠。
高频端(>400 Hz)出现轻微起伏,幅度约 ±1×10⁻³ V²/Hz,源于 Welch 分段平均的随机误差;增加分段长度或平均次数可进一步抑制起伏。
无明显离散谱线,再次验证信号的平坦谱特性。
(4)概率密度
直方图与红色理论高斯 PDF 曲线高度重合,对称钟形、尾部衰减迅速。
四、总结
(1)信号产生:利用 NumPy 的伪随机数发生器可快速、可复现地生成大量高斯白噪声样本,代码简洁、跨平台兼容性好。
(2)统计估计:在 10 k 点样本、1 kHz 采样率条件下,样本均值误差仅 0.02 V,方差误差 1.3 %;自相关函数在零滞后处呈现 4.05 V² 尖峰,其余滞后接近零;功率谱密度在 0--500 Hz 范围内保持 4×10⁻³ V²/Hz 的平坦特性,与理论值高度一致。
(3)误差分析:有限样本带来的随机起伏符合 1/√N 规律;通过增加样本长度或 Welch 分段平均次数,可进一步抑制 PSD 估计方差。
(4)工程意义:验证了经典随机信号估计方法的有效性,为后续自适应滤波、谱分析、系统辨识等实验奠定了理论与代码基础。
实验报告要求
(1)用 M atlab /Python 实现高斯随机信号;
(2)估计随机信号的期望、方差、自相关函数和功率谱密度(画图);
(3)将估计值和理论值进行比较。