机器学习：逻辑回归

逻辑回归
逻辑回归的实现
- 使用Sklearn实现
- 使用pytorch实现

逻辑回归

逻辑回归的概念

逻辑回归，虽然名字中含有"回归"，但确是一种"分类"算法，其通常用于解决二分类问题 。主要的思想为：在线性回归的基础上，拟合出来的值经过sigmoid函数映射为概率。
s i g m o i d = 1 1 + e − w T x + b sigmoid=\frac{1}{1+e^{-{\rm{w^Tx}+b}}} sigmoid=1+e−wTx+b1

其中， w T x + b \rm{w^Tx+b} wTx+b为一个线性函数
s i g m o i d sigmoid sigmoid函数将这个线性函数的结果映射为(0,1)之间的概率，从而进行分类。

逻辑回归处理多分类问题

逻辑回归一般是来处理二分类的问题，和SVM(支持向量机)类似，只不过逻辑回归的思想是找到一个边界，使其能够更加准确的判断样本点所处的类别的概率值。而SVM的思想则是找到一个超平面，使两个类别的边界样本距离该超平面的距离最大化。

逻辑回归一般用来处理二分类的问题，但是对于多分类的问题，逻辑回归依旧能解决。以三分类为例：

前提：现有三个类别 A ， B ， C A，B，C A，B，C

则此时建立三个逻辑回归，而每个逻辑回归分类器只做二分类问题。

对应分类器1，主要计算类别是 A A A和非 A A A(即类别 B B B或 C C C)的概率；

对应分类器2，主要计算类别是 B B B和非 B B B(即类别 A A A或 C C C)的概率；

对应分类器3，主要计算类别是 C C C和非 C C C(即类别 A A A或 B B B)的概率。

三个分类器并行进行计算，得出属于每个类别的概率，从而进行多分类任务。

分类问题的评估

混淆矩阵

混淆矩阵展示了预测值和真实值之间的四种结果，具体如下

	预测为真	预测为假
真实为真	TP	FN
真实为假	FP	TN

准确率-accuracy

准确率用来衡量模型的整体预测能力。适用于样本分布均匀的情况下 ，在类别分布不均匀(如99%都是负样本，1%是正样本)时完全失效。
A c c u r a c y = T P + T N T P + T N + F P + F N Accuracy=\frac{TP+TN}{TP+TN+FP+FN} Accuracy=TP+TN+FP+FNTP+TN

精确率-precision

精确率主要用来衡量预测为真的样本中，有多少个实际为真？适用于样本分布不均匀的情况 。例如在垃圾邮件检测中，借助此指标评估，即有多少预测为垃圾邮件的是真正的垃圾邮件。
p r e c i s i o n = T P T P + F P precision=\frac{TP}{TP+FP} precision=TP+FPTP

召回率-recall

召回率又称为漏报率，即在真实为真的样本中，有多少个样本被找出来了？适用于样本分布不均匀的情况 。例如在癌症预测中，宁可误诊一些健康的人，也不能漏诊一个患癌的人。
r e c a l l = T P T P + F N recall = \frac{TP}{TP+FN} recall=TP+FNTP

F1-Score

F1-Score是指精确率和召回率的调和平均。在两者间寻求平衡。
F 1 − S c o r e = 2 × P r e c i s i o n × R e c a l l P r e c i s i o n + R e c a l l F1-Score = 2\times \frac{Precision \times Recall}{Precision+Recall} F1−Score=2×Precision+RecallPrecision×Recall

ROC曲线与AUC值

ROC曲线展示在不同阈值下，真正例率(Recall)和假正例率的关系。而AUC则为ROC曲线下的面积。通常对AUC做以下评估：

AUC=0.5:模型无评估能力(随机瞎猜)
AUC>0.8:通常认为模型评估能力较好
AUC=1:完美模型

对数损失

在训练过程中，评估模型预测值和真实值之间的误差，可以使用对数损失进行衡量。
L o g L o s s = − 1 N ∑ i = 1 N [ ( y i l o g ( p i ) + ( 1 − y i ) l o g ( 1 − p i ) ] LogLoss = -\frac1N \sum_{i=1}^N [(y_i \mathrm{log} (p_i)+(1-y_i)\mathrm{log}(1-p_i)] LogLoss=−N1i=1∑N[(yilog(pi)+(1−yi)log(1−pi)]

逻辑回归的实现

使用Sklearn实现

python 复制代码

# 1.sklearn实现逻辑回归
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score,recall_score,precision_score,confusion_matrix,classification_report,f1_score
# 1.加载数据
iris = load_iris()
X = iris['data']
y = (iris.target==0).astype('int')   # iris数据集有三类'setosa' 'versicolor' 'virginica',这里转换为二分类问题，即是否为山鸢尾setosa
# 2.数据集划分
X_train,X_test,y_train,y_test = train_test_split(X,y,shuffle=True)
# 3.创建并训练模型
model = LogisticRegression(
    penalty='l2',
    C=1.0,
    solver='lbfgs',
    max_iter=100
)
model.fit(X_train,y_train)
# 4.预测并评估
y_pred = model.predict(X_test)
y_proba = model.predict_proba(X_test)[:,1]
print(f'准确率:{accuracy_score(y_test,y_pred):.3f}')
print(f'\n混淆矩阵:\n{confusion_matrix(y_test,y_pred)}')
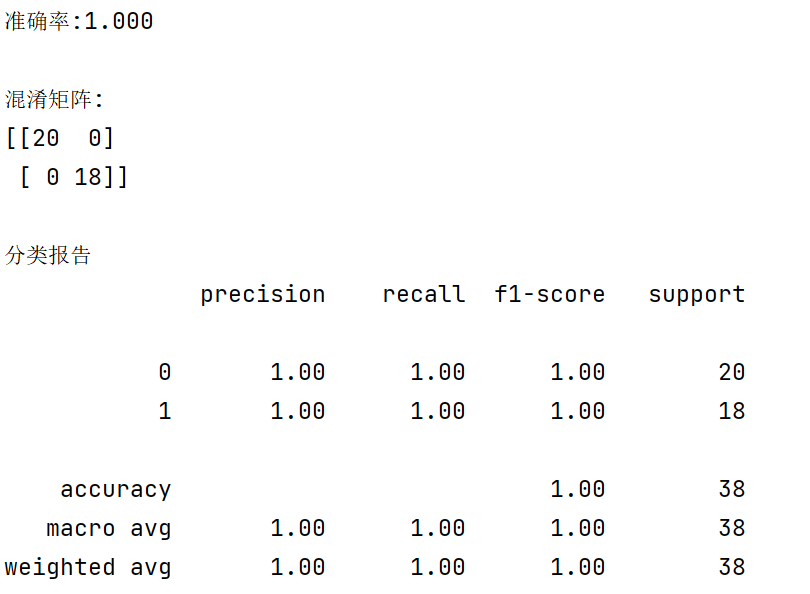
print(f'\n分类报告\n{classification_report(y_test,y_pred)}')

输出结果如下：

使用pytorch实现

bash 复制代码

# pytorch实现逻辑回归
import torch
import torch.nn as nn
import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix,accuracy_score,recall_score,precision_score
import torch.optim as optim
import matplotlib.pyplot as plt
# 1.生成一个2个特征,2个类别的样本
np.random.seed(42)
X,y = make_classification(n_samples=1000,n_features=2,n_redundant=0,n_classes=2,random_state=42)
X = X.astype(np.float32)
y = y.astype(np.float32)
X_train,X_test,y_train,y_test = train_test_split(X,y,shuffle=True)
# 2.转换为tensor类型
X_train_tensor = torch.from_numpy(X_train).float()
X_test_tensor = torch.from_numpy(X_test).float()
y_train_tensor = torch.from_numpy(y_train).float().view(-1,1)
y_test_tensor = torch.from_numpy(y_test).float().view(-1,1)
# 3.定义网络
class LogicalRegression(nn.Module):
    def __init__(self,in_dims):
        super().__init__()
        self.linear = nn.Linear(in_dims,1)
    def forward(self,x):
        output = self.linear(x)
        return torch.sigmoid(output)
# 4.定义优化器、损失函数
in_dims = X.shape[1]
model = LogicalRegression(in_dims=in_dims)
optimizer = optim.Adam(model.parameters(),lr=0.01)
criterion = nn.BCELoss()
losses = []
# 5.训练网络
epochs = 1000
for epoch in range(epochs):
    # 前向传播
    output = model(X_train_tensor)
    loss = criterion(output,y_train_tensor)
    # 后向传播
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    losses.append(loss.item())
    if (epoch+1)%100==0:
            print(f'{epoch+1}/{epochs},loss={loss:.3f}')
with torch.no_grad():
    y_pred = model(X_test_tensor)
    # 转换为分类模型
    y_pred_class = (y_pred>0.5).int()
    print(f'模型预测准确率:{accuracy_score(y_test_tensor,y_pred_class)}')  # 准确率:(TP+FN)/(TP+TN+FP+FN)
    print(f'召回率为:{recall_score(y_test_tensor,y_pred_class)}')     # 召回率:TP/(TP+TN)
    print(f'精确率为:{precision_score(y_test_tensor,y_pred_class)}')  # 精确率:TP/(TP+FP)
    print(f'混淆矩阵:\n{confusion_matrix(y_test_tensor,y_pred_class)}')
    # 绘制图像
    plt.figure(figsize=(12,5))
    # 损失曲线
    plt.plot(losses)
    plt.title('Training Loss')
    plt.xlabel('Epoch')
    plt.ylabel('Loss')
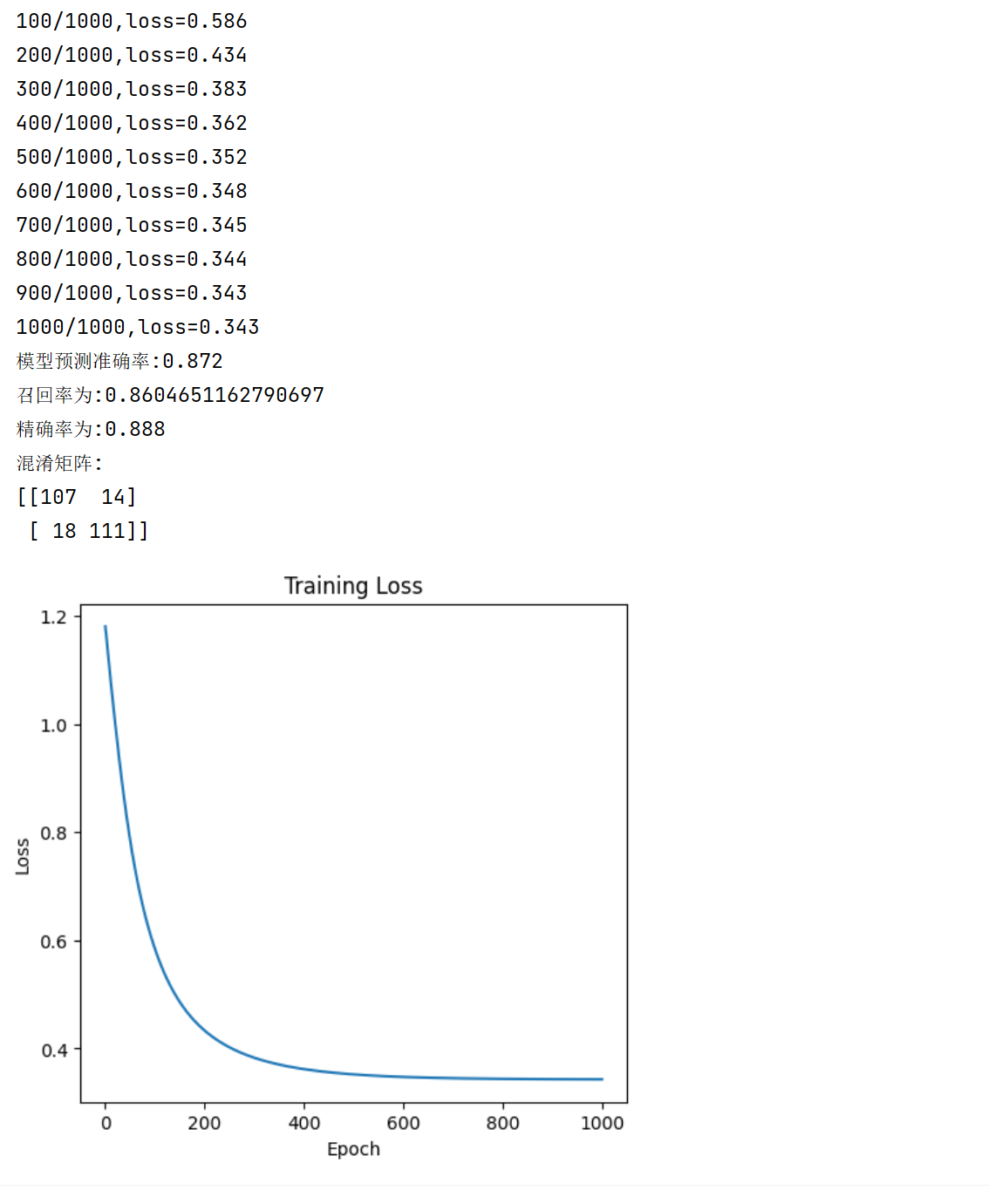
    plt.show()

输出如下：