LeetCode:90.最长有效括号

目录

1.最长有效括号

---

1.最长有效括号

设dpi表示以i位置结尾的最长有效括号长度，假设i位置为'），可以分为以下两种情况：

1. i - 1位置为（，那么i - 1和i位置刚好可以拼接为一个有效括号长度为2，如果i - 2位置还有括号的话，那么dpi = dpi - 2 + 2，下面用一张图来表示
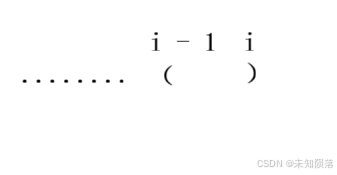
2. i - 1的位置为），如果dpi - 1 >= 0的话，表示前面还有有效括号，并且i - dpi - 1 - 1 >= 0,i - dpi - 1 - 1的位置为（，dpi = dpi - 1 + 2,如果i - dpi - 1 - 2 >= 0的话，dpi = dpi - 1 + 2 + dpi - dp\[i - 1 - 2]，下面用图表示

class Solution {
public:
    int longestValidParentheses(string s) {
        int n = s.size();
        vector<int> dp(n);
        int length = 0;
        for(int i = 1; i < n; i++)
        {
            if(s[i] == ')')
            {
                if(s[i - 1] == '(')
                {
                    dp[i] = 2;
                    if(i - 2 >= 0)
                        dp[i] = dp[i - 2] + dp[i];
                }
                else
                {
                    if(dp[i - 1] >= 0)
                    {
                        if(i - dp[i - 1] - 1 >= 0 && s[i - dp[i - 1] - 1] == '(')
                        {
                            dp[i] = dp[i - 1] + 2;
                            if(i - dp[i - 1] - 2 >= 0)
                                dp[i] = dp[i] + dp[i - dp[i - 1] - 2];
                        }
                    }
                }
            }
            length = max(length, dp[i]);
        }
        return length;
    }
};