Week 19: 深度学习补遗：自注意力和Transformer Encoder架构

Week 19: 深度学习补遗：自注意力和Transformer Encoder架构

摘要

本周主要跟随李宏毅老师的课程进行学习，对自注意力的知识进行了深化学习和理解，并且开始了对于Transformer的模型的学习。

Abstract

This week's learning primarily followed Professor Hung-yi Lee's course, deepening my knowledge and understanding of self-attention mechanisms while also initiating the study of Transformer models.

1. Self-Attention 自注意力

自注意力机制对比其他前后文时序模型，例如RNN、LSTM等的显著优势之一是其并行性，即不再需要串行地依赖前文的计算用于后文计算，而是可以并行地计算所有元素的注意力分数。
qi=Wqaiki=Wkaivi=Wvai q^i=W^qa^i \\ k^i=W^ka^i \\ v^i=W^va^i qi=Wqaiki=Wkaivi=Wvai

因为每一个qiq^iqi、kik^iki、viv^ivi都是aia^iai乘以对应的矩阵运算得到的，于是，可以考虑将aia^iai矩阵拼接，变为III。直接进行矩阵乘法，一次性计算出结果。那么 qiq^iqi、kik^iki、viv^ivi将会对应变为QQQ、KKK、VVV。而其中的转换矩阵WqW^qWq、WkW^kWk、WvW^vWv是需要被学习的参数。
Q‾Query Matrix=WqI‾Input Vector MatrixK‾Key Matrix=WkI‾Input Vector MatrixV‾Value Matrix=WvI‾Input Vector Matrix \underset{\text{Query Matrix}}{\underline{Q}}=W^q\underset{\text{Input Vector Matrix}}{\underline{I}}\\ \underset{\text{Key Matrix}}{\underline{K}}=W^k\underset{\text{Input Vector Matrix}}{\underline{I}}\\ \underset{\text{Value Matrix}}{\underline{V}}=W^v\underset{\text{Input Vector Matrix}}{\underline{I}}\\ Query MatrixQ=WqInput Vector MatrixIKey MatrixK=WkInput Vector MatrixIValue MatrixV=WvInput Vector MatrixI

完成了QQQ、KKK、VVV的计算后，就可以进一步利用矩阵运算计算注意力分数。
A′‾Attention Matrix←Some ModificationA=KTQO‾Output Matrix=VA′ \underset{\text{Attention Matrix}}{\underline{A'}}\underset{\text{Some Modification}}{\gets} A=K^TQ\\ \underset{\text{Output Matrix}}{\underline{O}}=VA' Attention MatrixA′Some Modification←A=KTQOutput MatrixO=VA′

2. Multi-head Self-Attention 多头自注意力

有时问题会有很多个尺度的信息，单个注意力头并不足够提取全局特征，可能就需要多个注意力头对全局特征进行提取。在一些场景下，例如翻译、语义解析等，多头注意力能显著取得更好的效果。

多头注意力机制指的是有多个并行的注意力头，使用不同的权重和转换矩阵以提取序列不同维度的信息。

以两头自注意力机制为例，在求解qi,1q^{i,1}qi,1时，使用Wq,1W^{q^,1}Wq,1权重矩阵；而在求解qi,2q^{i,2}qi,2时，使用Wq,2W^{q^,2}Wq,2权重矩阵。
qi,1=Wq,1qiqi,2=Wq,2qi q^{i,1}=W^{q,1}q^i \\ q^{i,2}=W^{q,2}q^i qi,1=Wq,1qiqi,2=Wq,2qi
kkk、vvv同理，同时根据相同头一起计算的原则，与自注意力一样的步骤计算出kkk、vvv、aaa和bi,1b^{i,1}bi,1与bi,2b^{i,2}bi,2。

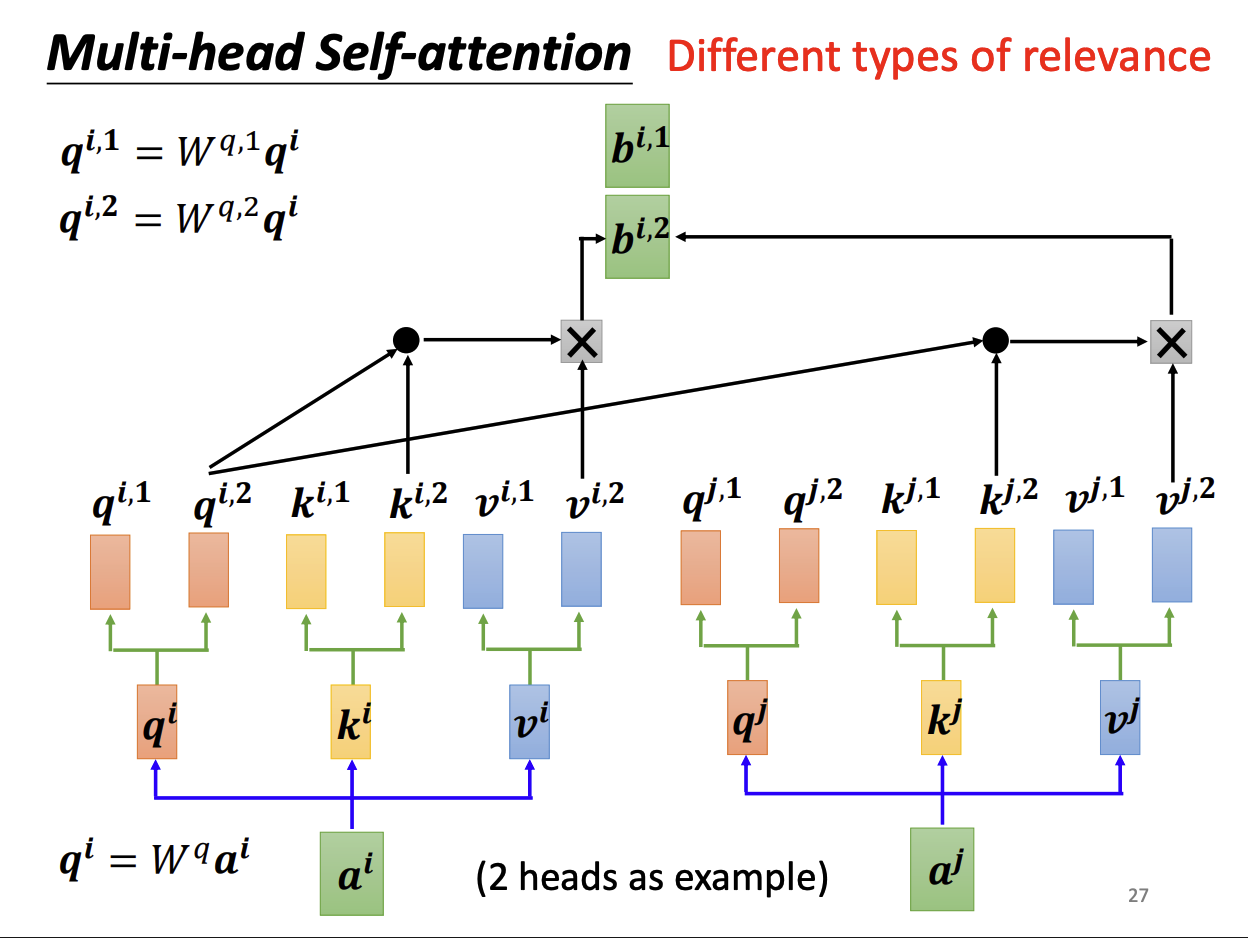
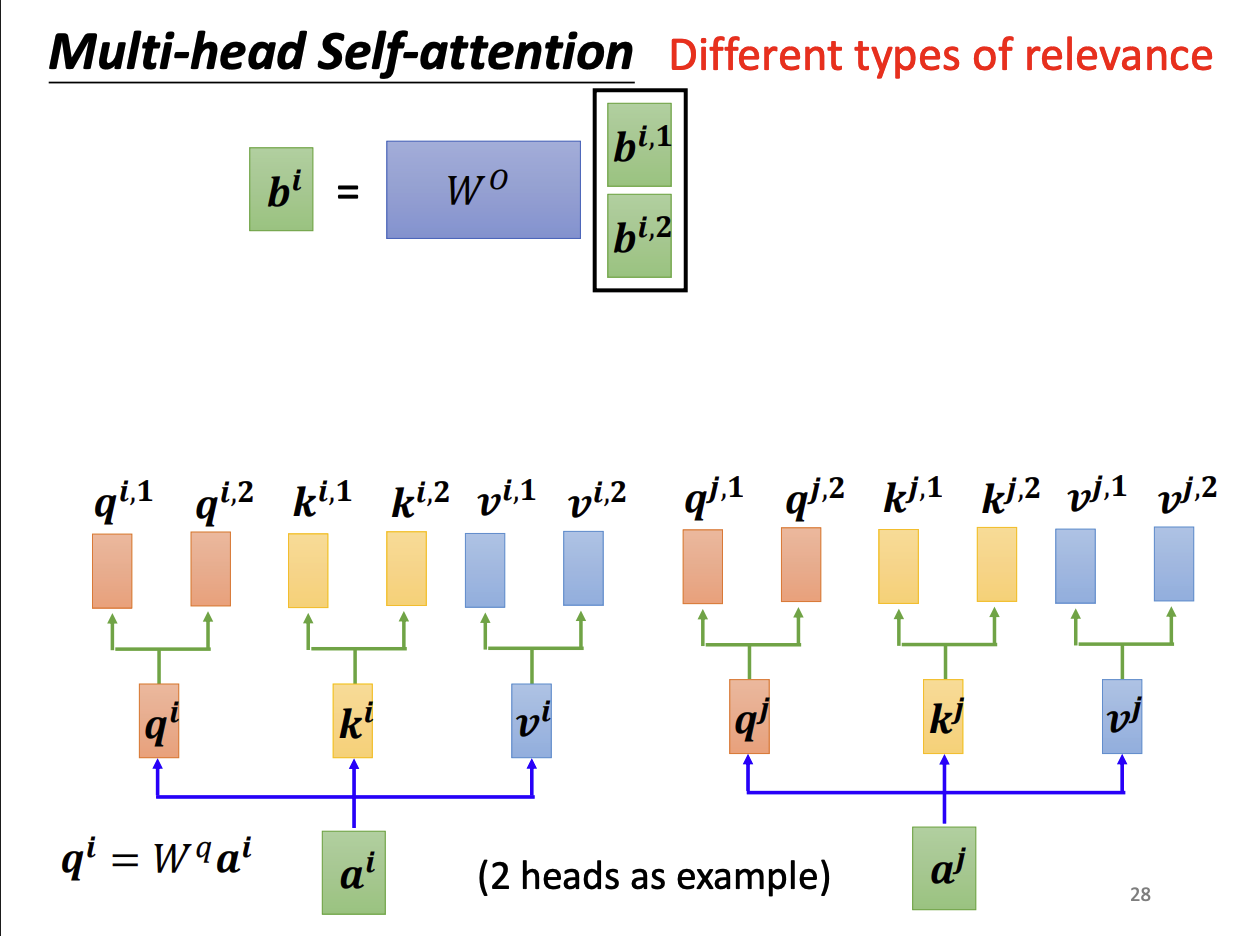
最后，纵向拼接bi,1b^{i,1}bi,1与bi,2b^{i,2}bi,2，乘一个转换矩阵WOW^OWO后得到原来单头注意力输出的bib^ibi。

3. Positional Encoding 位置编码

在自注意力里，没有位置信息嵌入，位置对每个输出没有影响。位置编码对每一个位置设定一个位置向量（Positional Vector）eie^iei。
ei+ai‾qikivi e^i+\underset{q^i\quad k^i \quad v^i}{\underline{a^i}} ei+qikiviai

直接将位置编码加上即可完成对位置信息的嵌入，在"Attention is all you need"原论文中，使用了一种利用三角函数生成位置向量的方法。实际上位置向量可以既可以采用三角函数生成（Sinusoidal），也可以利用神经网络进行嵌入，还可以自己设计生成规则。

4. Transformer架构初探

Transformer是一个开创性的Seq2Seq架构，同时也是一个Encoder-Decoder设计的模型。

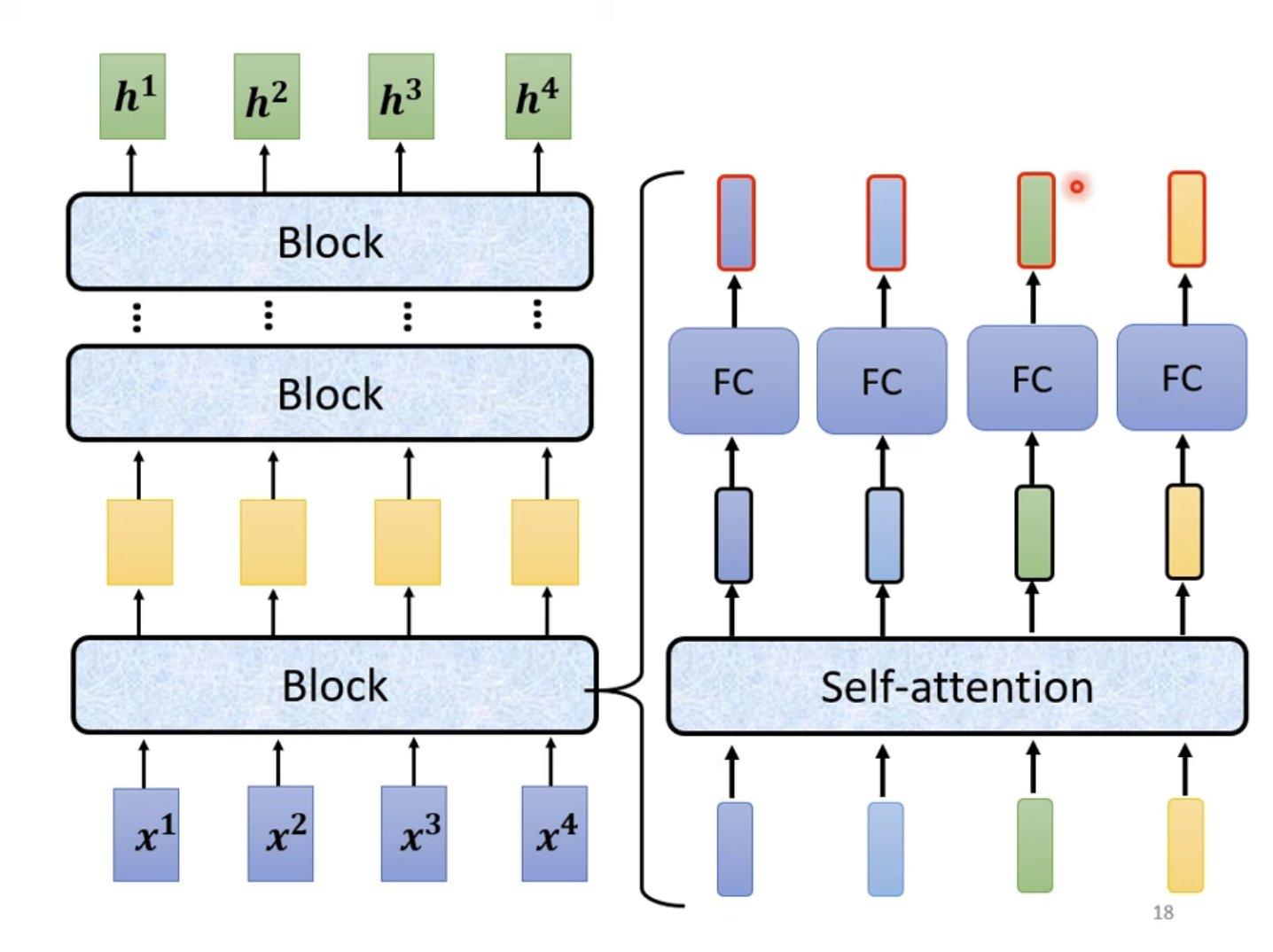
对于一个复杂的模型，通常架构由数个Block组成，由一组向量输入，输出相同维度的一组向量进入下一个Block......之所以不将一个Block称为一个Layer，是因为一个Block实际上是由多个Layer组合而成的，并不是单一的Layer的作用。

5. Residual Connection 残差链接

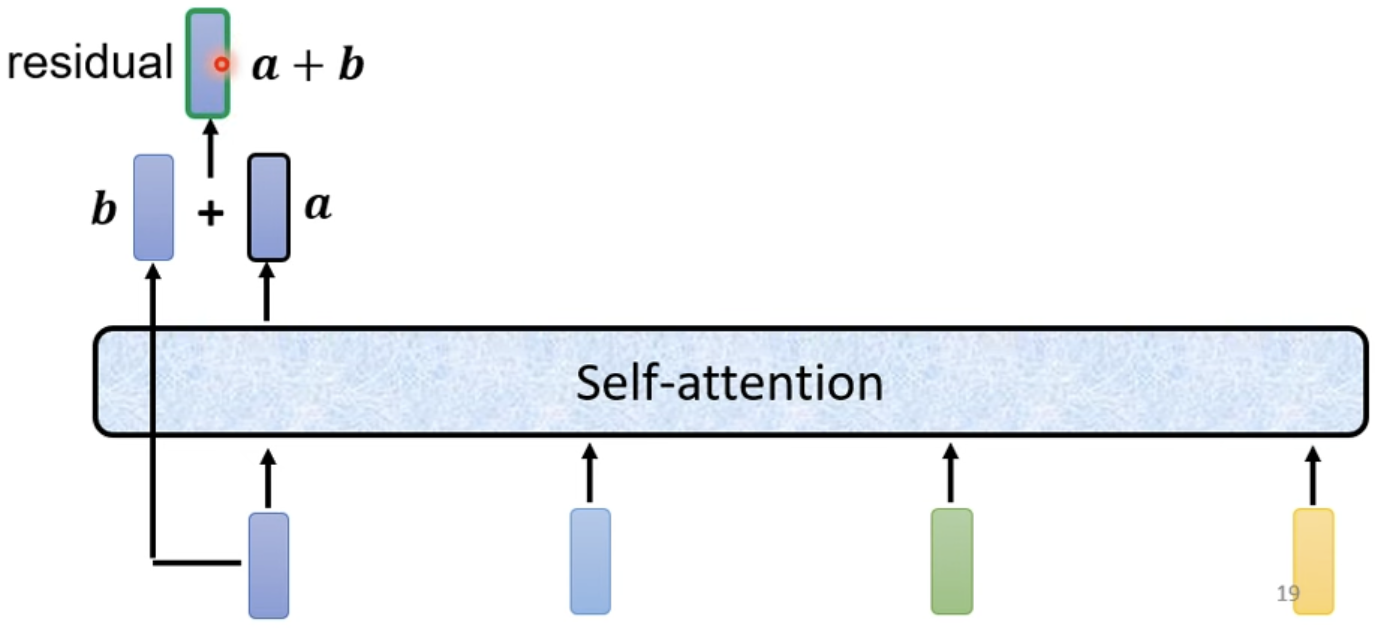
Transformer中的自注意力机制有特殊的设计，使用了残差连接机制。即对于自注意力层的输出aaa再加上其输入bbb，以a+ba+ba+b作为自注意力层输出的结果。在Transformer中，大量使用了残差链接机制。

6. Layer Normalization 层归一化

与常用的Batch Normalization 批归一化不同，Transformer使用了层归一化，更加简单。批归一化做的是对于不同的样本、不同的特征的同一个维度进行归一化，而层归一化是对于相同的样本、相同的特征的不同维度进行归一化。

层归一化首先要计算层输出的均值mmm与标准差σ\sigmaσ，归一化的结果xi′=xi−mσx_i^{'}=\frac{x_i-m}{\sigma}xi′=σxi−m。

在Transformer中的"Add+Norm"层指的就是残差连接与层归一化。

7. Transfomer Encoder 总览

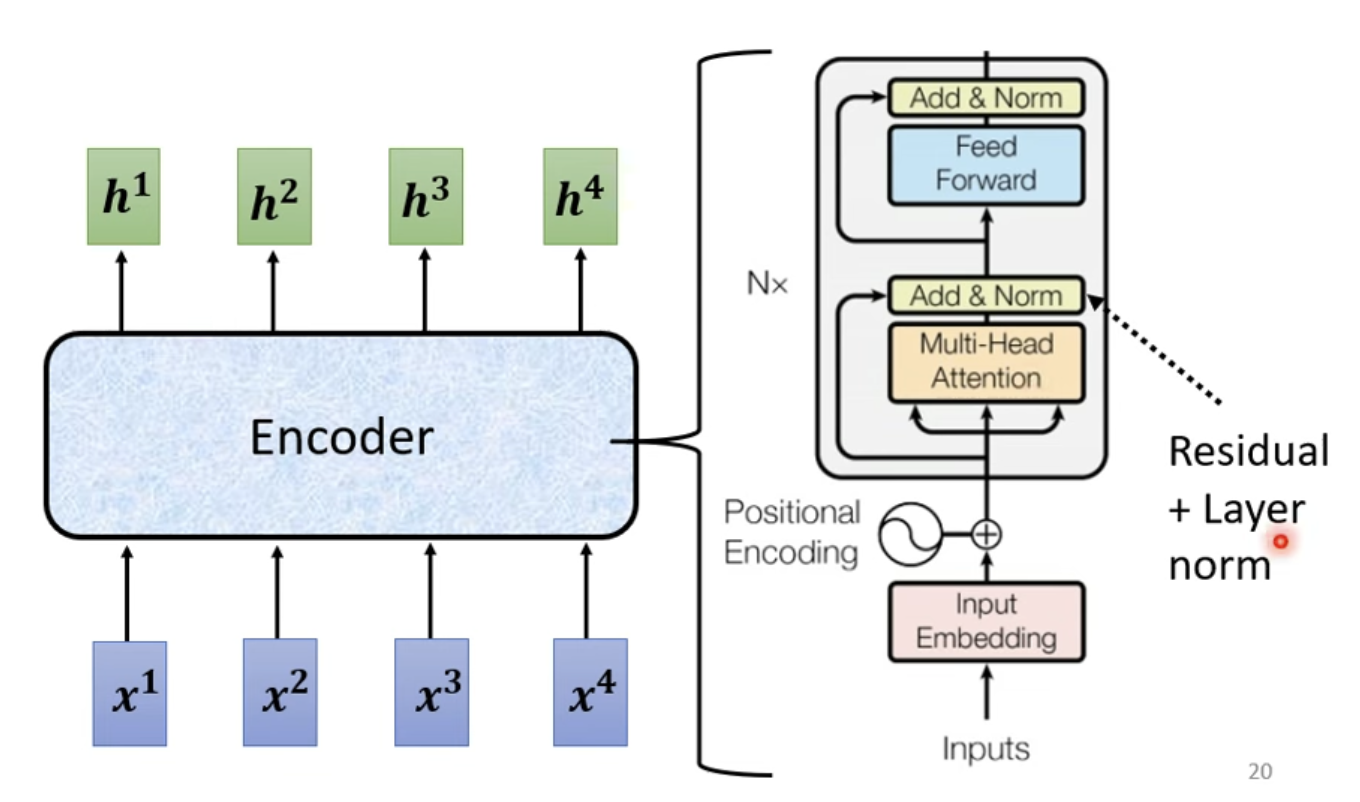
简要来讲，每个Transformer的Encoder Block都由这个架构组成，输入经过嵌入后加上位置编码，通往多头注意力机制并予以残差连接和层归一化，最后输入前馈神经网络（全连接层）同时予以残差连接和层归一化，完成一个Encoder的输出。

总结

本周对自注意力机制的批量运算数学机制进行了学习，并且对Transformer开始了探究。对Transformer几个关键机制进行了了解，例如残差连接与层归一化等机制，预计下周对Transformer Decoder等相关机制进行探索和学习。