Leetcode刷题 - 技术栈

一、链表中的环问题

[141. 环形链表：判断链表是否有环](#141. 环形链表：判断链表是否有环)

[142. 环形链表 II：找到入环的第一个节点](#142. 环形链表 II：找到入环的第一个节点)

二、字符串处理问题

[942. 增减字符串匹配](#942. 增减字符串匹配)

[409. 最长回文串](#409. 最长回文串)

[三、数组贪心问题：870. 优势洗牌](#三、数组贪心问题：870. 优势洗牌)

总结

在算法学习的路上，刷题是提升能力的关键途径。今天我们来剖析几道经典的算法题目，涵盖链表、字符串、数组等多个领域，一起看看它们的解题思路和代码实现。

一、链表中的环问题

141. 环形链表：判断链表是否有环

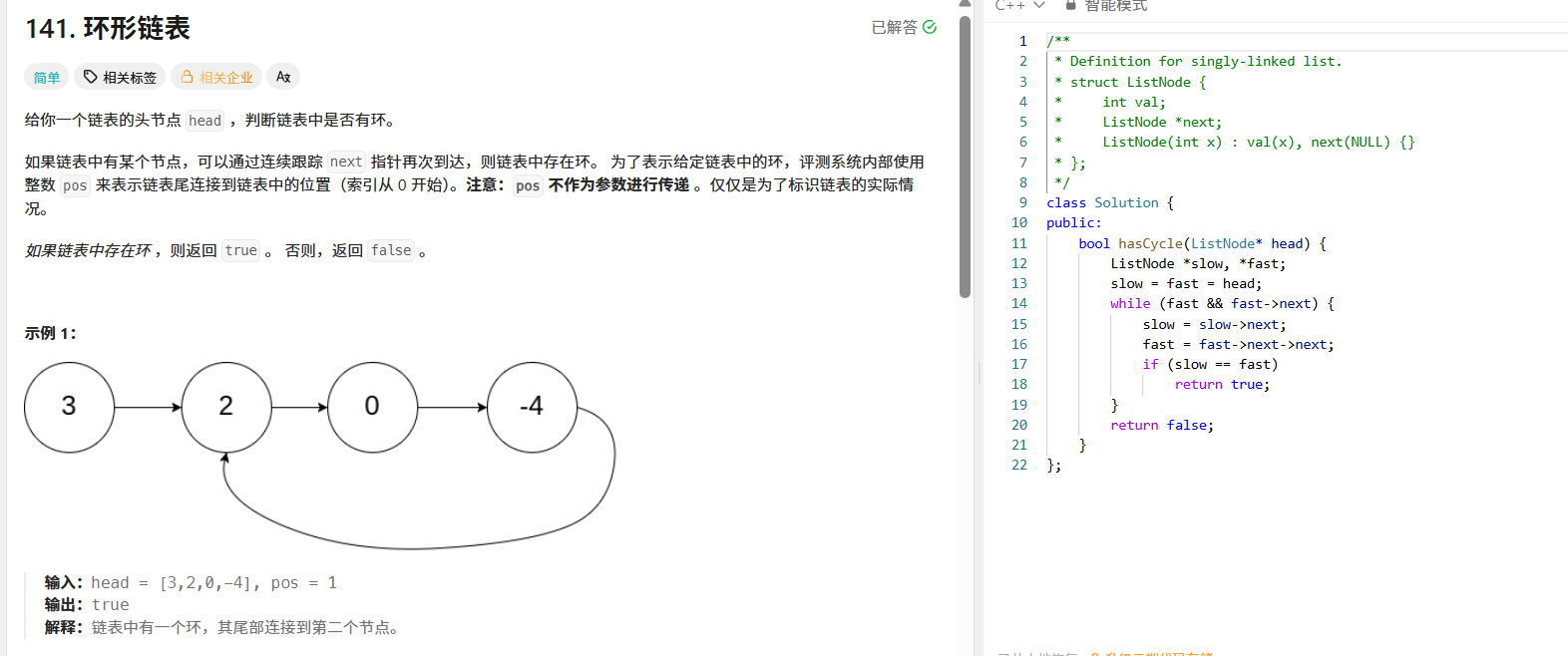
这道题可以用快慢指针法（龟兔赛跑算法）来解决。我们定义两个指针，慢指针一次走一步，快指针一次走两步。如果链表中存在环，那么快慢指针最终一定会相遇；如果快指针走到了链表末尾（ null ），则说明链表无环。

cpp 复制代码

class Solution {
public:
    bool hasCycle(ListNode* head) {
        ListNode *slow, *fast;
        slow = fast = head;
        while (fast && fast->next) {
            slow = slow->next;
            fast = fast->next->next;
            if (slow == fast)
                return true;
        }
        return false;
    }
};

142. 环形链表 II：找到入环的第一个节点

这道题是上一题的进阶。当快慢指针相遇后，我们再定义一个指针从链表头出发，慢指针继续从相遇点出发，两者每次都走一步，最终相遇的节点就是入环的第一个节点。

原理是：设链表头到入环点的距离为 a ，环的长度为 b 。快慢指针相遇时，慢指针走了 a + x ，快指针走了 a + x + nb （ n 是快指针绕环的圈数）。又因为快指针速度是慢指针的两倍，所以 2(a + x) = a + x + nb ，化简得 a = nb - x 。这意味着从头节点和相遇点同时出发的指针，会在入环点相遇。

cpp 复制代码

class Solution {
public:
    ListNode* detectCycle(ListNode* head) {
        ListNode *fast, *slow;
        slow = fast = head;
        while (fast && fast->next) {
            fast = fast->next->next;
            slow = slow->next;
            if (fast == slow) {
                ListNode* index1 = fast;
                ListNode* index2 = head;
                while (index1 != index2) {
                    index1 = index1->next;
                    index2 = index2->next;
                }
                return index1;
            }
        }
        return nullptr;
    }
};

二、字符串处理问题

942. 增减字符串匹配

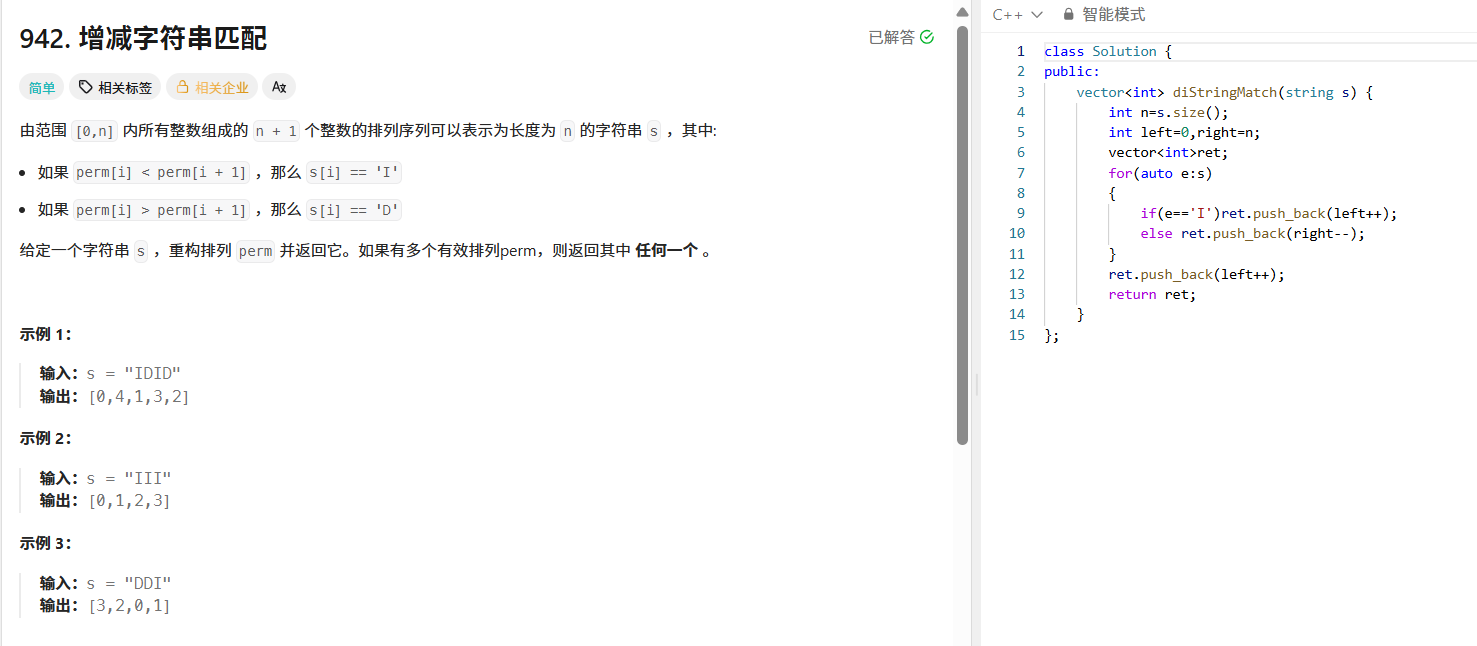
这道题可以用双指针贪心的思路解决。我们定义 left 指针指向当前可用的最小数， right 指针指向当前可用的最大数。遍历字符串 s ：

若当前字符是 'I' ，说明下一个数要比当前大，所以选当前最小的数 left ，并将 left 右移；
若当前字符是 'D' ，说明下一个数要比当前小，所以选当前最大的数 right ，并将 right 左移；
最后把剩下的那个数加入结果即可。

cpp 复制代码

class Solution {
public:
    vector<int> diStringMatch(string s) {
        int n = s.size();
        int left = 0, right = n;
        vector<int> ret;
        for (auto e : s) {
            if (e == 'I') ret.push_back(left++);
            else ret.push_back(right--);
        }
        ret.push_back(left++);
        return ret;
    }
};

409. 最长回文串

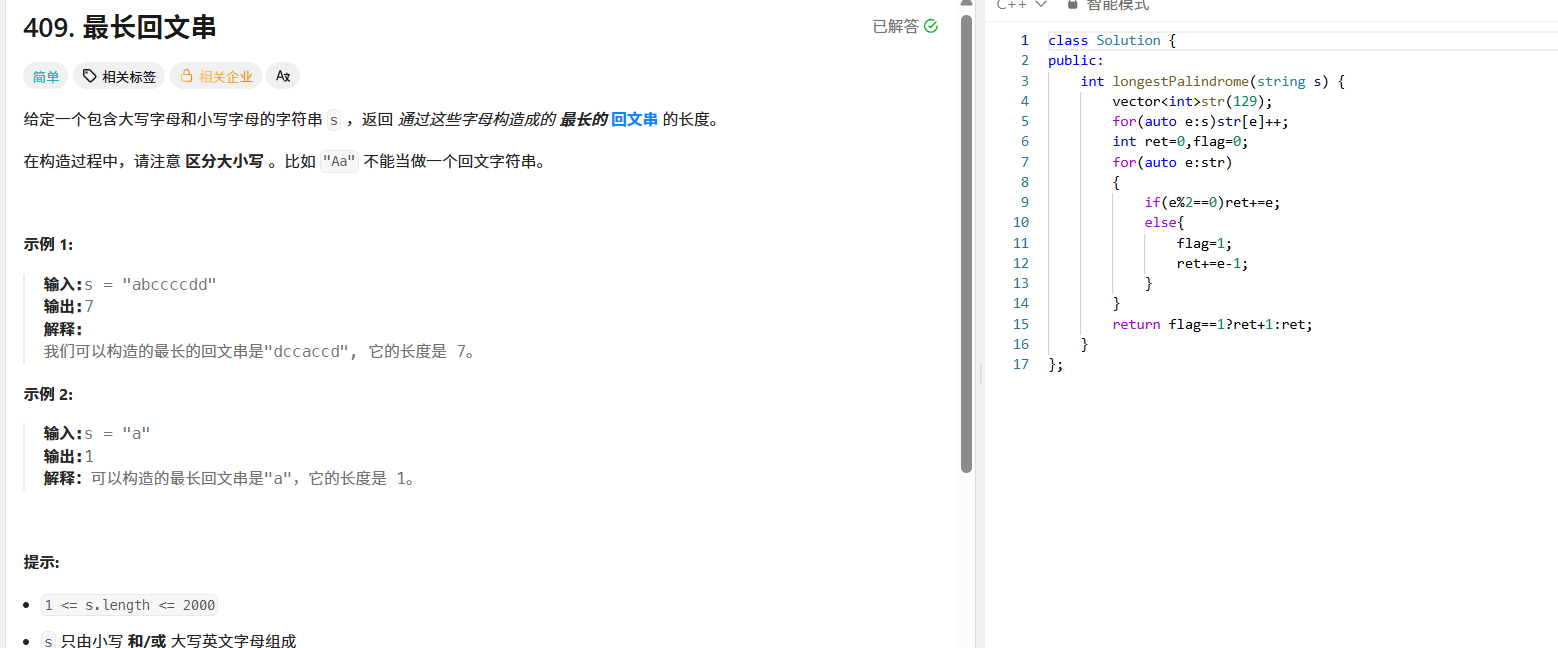
回文串的特点是对称，所以我们可以统计每个字符出现的次数。对于出现偶数次的字符，可以全部用来构造回文串；对于出现奇数次的字符，我们可以用其偶数部分，并且最多可以保留一个奇数次数的字符作为回文串的中心。

cpp 复制代码

class Solution {
public:
    int longestPalindrome(string s) {
        vector<int> str(129); // 涵盖大小写字母的ASCII范围
        for (auto e : s) str[e]++;
        int ret = 0, flag = 0;
        for (auto e : str) {
            if (e % 2 == 0) ret += e;
            else {
                flag = 1;
                ret += e - 1;
            }
        }
        return flag ? ret + 1 : ret;
    }
};

三、数组贪心问题：870. 优势洗牌

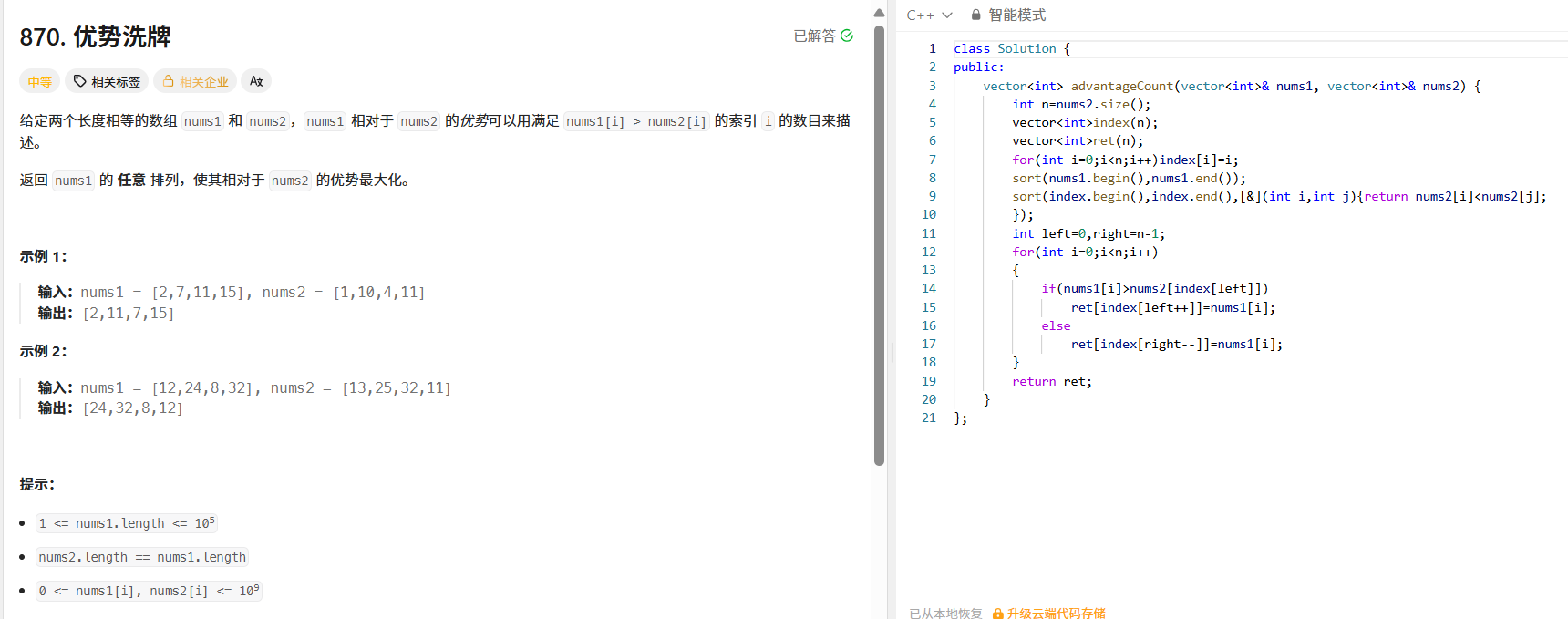
这道题的核心是最大化优势，即让 nums1 中尽可能多的元素大于 nums2 中对应位置的元素。我们可以用排序和双指针的方法：

先对 nums1 排序，再对 nums2 按元素大小排序（同时记录原始索引）；
用双指针分别指向 nums1 的头和 nums2 的头/尾：如果 nums1 的当前最小值大于 nums2 的当前最小值，就将这两个元素匹配；否则，将 nums1 的当前最小值与 nums2 的当前最大值匹配，这样可以尽可能保留 nums1 中较大的元素去匹配 nums2 中较小的元素。

cpp 复制代码

class Solution {
public:
    vector<int> advantageCount(vector<int>& nums1, vector<int>& nums2) {
        int n = nums2.size();
        vector<int> index(n);
        vector<int> ret(n);
        for (int i = 0; i < n; i++) index[i] = i;
        sort(nums1.begin(), nums1.end());
        // 对nums2的索引按nums2元素大小排序
        sort(index.begin(), index.end(), [&](int i, int j) { return nums2[i] < nums2[j]; });
        int left = 0, right = n - 1;
        for (int i = 0; i < n; i++) {
            if (nums1[i] > nums2[index[left]]) {
                ret[index[left++]] = nums1[i];
            } else {
                ret[index[right--]] = nums1[i];
            }
        }
        return ret;
    }
};

总结

以上几道题涵盖了快慢指针、贪心、哈希统计等多种算法思想。在刷题时，我们要注重理解题目的本质，提炼解题模型，这样才能在遇到类似问题时举一反三。希望这篇笔记能对大家的算法学习有所帮助，一起加油刷题吧！