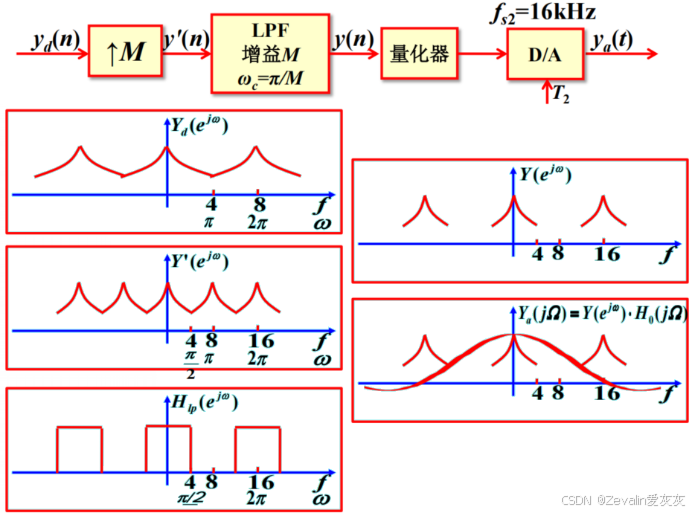
一、信号的整数倍抽取
1、问题引入
(1)研究多采样率信号处理的原因:
①数字传输系统应具有传输多种抽样率信号(比如语音信号和视频信号)并自动地完成抽样率转换的能力。
②频信号的处理和应用中目前存在着多种抽样频率,例如,立体声音频信号采样频率是48 kHz,CD是44.1 kHz,而数字音频广播是32 kHz。
③将数字信号在两个具有独立时钟的数字系统之间传递时,要求该数字信号的抽样率能根据时钟的不同而转换。
④用具有不同频带的低通、带通及高通滤波器对信号做子带分解,对分解后的信号再做抽样率转换及特征提取,可以最大限度地减少数据量,实现数据压缩的目的。
⑤对一个信号抽样时,若抽样率过高,必然会造成数据的冗余,这时希望能将该数字信号的抽样率减下来。
(2)以上几个方面都是希望能对抽样率进行转换,或要求数字系统能工作在多抽样率状态,因此,建立在抽样率转换理论及其系统实现基础上的多抽样率数字信号处理已成为现代信号处理的重要内容。
2、信号的整数倍抽取过程
(1)抽取前后时域和频域的变化:

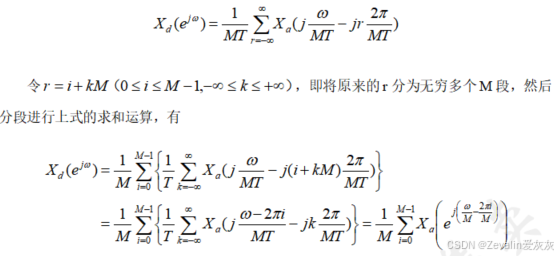
(2)举例:
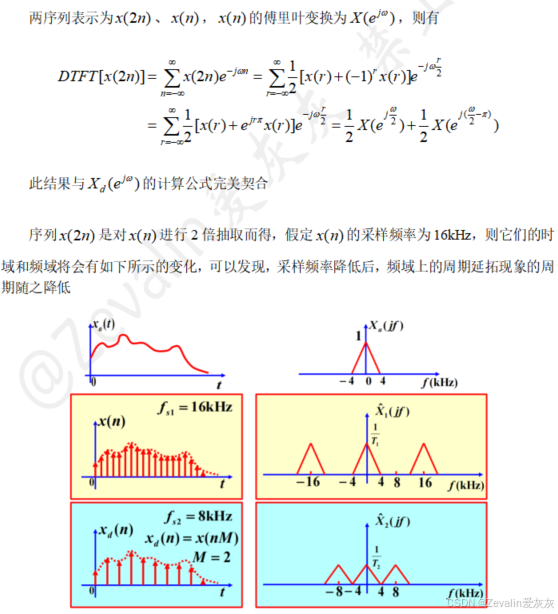
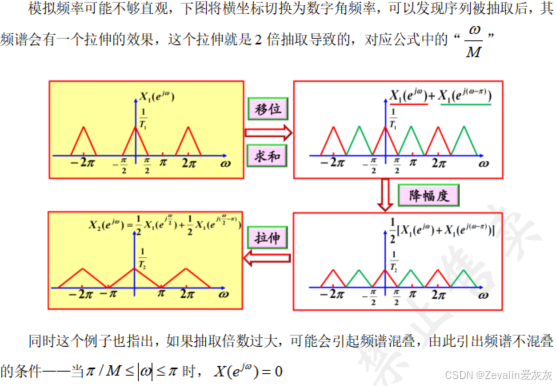
3、抽取滤波器(抗混叠滤波器)与抽取器级联

二、信号的整数倍内插
1、信号的整数倍内插过程
(1)内插前后时域和频域的变化:

(2)举例:
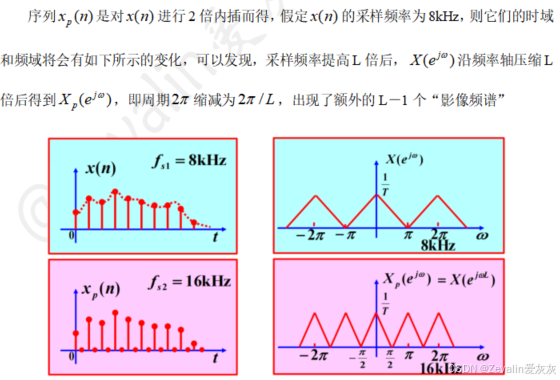
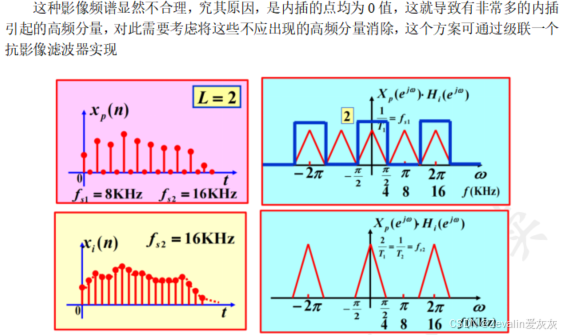
2、内插器与内插滤波器(抗影像滤波器)级联

三、信号的任意有理数倍采样频变换及应用
1、单级采样频率变换
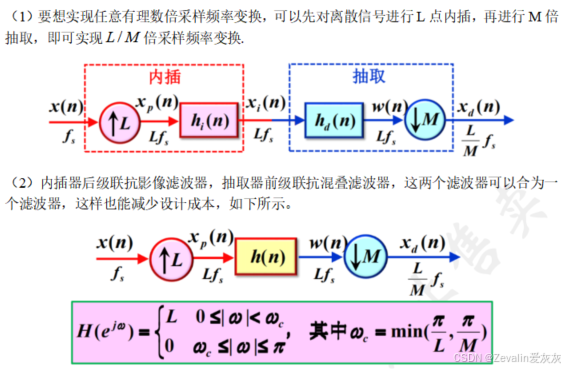
2、多级采样频率变换
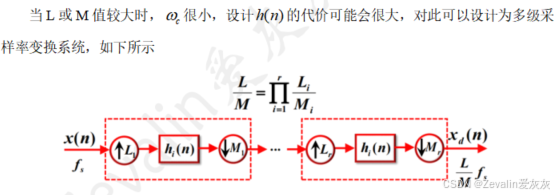
3、多采样率系统的应用举例
(1)语音系统中的应用:
语音系统往往需要处理各种频率的音频信号,它对抗混叠的需求也会比较高,然而理想的抗混叠滤波器(即使设计为模拟滤波器)很难实现,这就导致经过抗混叠滤波器处理过的信号仍然可能无法满足采样定理的要求
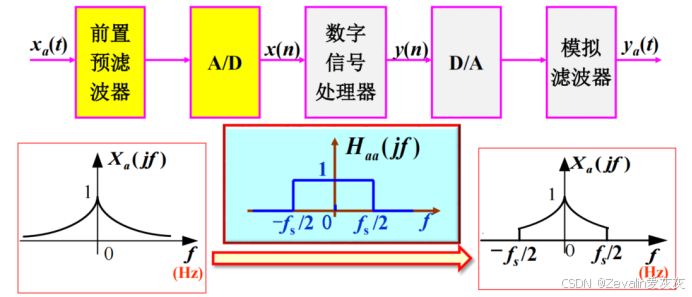
对此可考虑引入抽取系统,先让输入信号经过一个非理想的抗混叠滤波器,然后进行采样,采样后的信号必然会有频谱混叠现象,但只要保证混叠处的频率分量不是数字信号处理需要的频率分量,那么就可以使用一个截止频率为的数字低通滤波器将其滤除,然后再通过M倍抽取将频谱拉伸即可
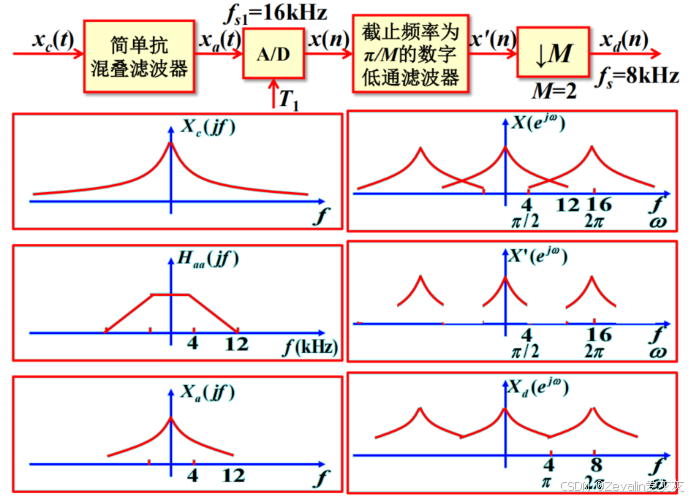
计算机的算力有时候不能满足输出语音序列采样频率的要求,这就导致输出的信号有很明显的"零阶保持"现象
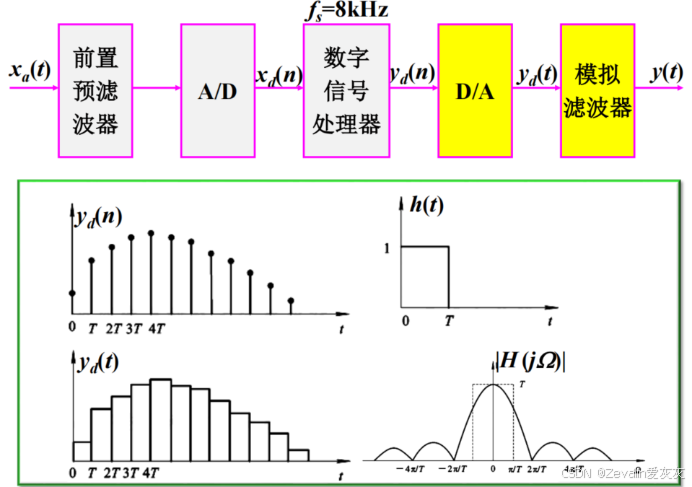
对此可考虑引入内插系统,在信号输出前对其进行内插处理,然后去除内插过程中产生的高频分量即可