文章目录


题目解析
题目描述:

示例 1:
输入:nums = [1]
输出:[2,3]
解释:n = 3(数组长度+2),[1,3] 中缺失的数字为 2 和 3
示例 2:输入:nums = [2,3]
输出:[1,4]
解释:n = 4(数组长度+2),[1,4] 中缺失的数字为 1 和 4
限制:
n >= 2(数组长度至少为 0,对应 n=2 时缺失 1 和 2)- 数组中所有元素均唯一且在
[1, n]范围内nums.length <= 30000
为什么这道题值得你花几分钟弄懂?
这道题是位运算经典场景的"组合升级题" ------它融合了力扣136. 丢失的数字 和 力扣260. 只出现一次的数字III 的核心逻辑。其价值不在于"暴力枚举找缺失",而在于掌握 "用异或拆分问题、精准定位目标"的高效思维,这是面试中考察"位运算深度应用"和"问题拆解能力"的高频考点。
面试官考察这道题时,核心关注三点:
- 能否联想到"异或的特性",将"找两个缺失数"转化为"找两个唯一出现一次的数",体现问题转化能力;
- 能否通过"异或结果的最低有效位"拆分集合,将两个目标数分离到不同组,暴露对位运算细节的掌握;
- 能否优化"找最低有效位"的代码(如用
sum & (-sum)),彰显对位运算技巧的熟练程度。
强烈建议先去看一看这两道题:
- 丢失的数字:用"异或数组元素+异或1~n"找1个缺失数;(注:这道题可以看一看这篇讲解博客 力扣 268. 丢失的数字 题解)
- 只出现一次的数字Ⅲ:用"异或拆分集合"找2个唯一出现一次的数。
算法原理
核心公式👇(详细推导可参考位运算 常见方法总结 算法练习):
x ^ x = 0
相同数字异或结果为 0:两个完全一致的二进制数,对应位完全相同,异或后每一位均为 0;
0 ^ x = x
0 与任何数字异或结果为该数字本身:0 的所有二进制位均为 0,与其他数字异或时,结果完全跟随另一数字的二进制位。
(tmp >> diff) & 1公式的作用是精准判断
tmp的二进制表示中,第diff位(从 0 开始计数)的数值是 0 还是 1。
1. 用异或得到"两个缺失数的异或结果"
结合题目场景来看:数组 nums 包含 n-2 个不同整数,且所有整数都在 [1, n] 范围内(其中 n = nums.size() + 2)。这意味着 [1, n] 中恰好有 2 个数字未出现在 nums 中,也就是我们要找的目标数(记为 a 和 b)所以我们就可以按照丢失的数字那道题的方法进行统计。
即我们可以将"数组元素"与"[1, n] 所有数字"视为一个完整的"对比集合",对两者进行全量异或:
- 对于
[1, n]中出现在nums里的数字 :它会在"数组元素异或"中出现 1 次,在"[1, n]数字异或"中也出现 1 次。根据x ^ x = 0,这两次异或会相互抵消,最终贡献为 0; - 对于
[1, n]中未出现在nums里的两个目标数a和b:它们仅在"[1, n]数字异或"中出现 1 次,在"数组元素异或"中完全未出现。根据0 ^ x = x,这两个数不会被抵消,最终会保留在异或结果中。
 因此,全量异或的最终结果,本质就是两个目标数的异或值,即
因此,全量异或的最终结果,本质就是两个目标数的异或值,即 tmp = a ^ b。
2. 找到异或结果中"最低为1的位",以此为依据拆分集合
首先要明确一个关键前提:第一步得到的异或结果 tmp = a ^ b(a、b 为两个缺失数)必然不为 0。
因为 a 和 b 是 [1, n] 中两个不同的数字,它们的二进制表示至少存在一处差异------而异或运算的核心特性是"对应位不同则为 1",这就意味着 tmp 的二进制中至少有一位是 1 (这一位正是 a 和 b 二进制差异的直接体现)。
接下来,我们需要定位到 tmp 中"最低为 1 的位",这里我们通过位运算公式 (tmp >> diff) & 1:
- 通过逐步增大
diff(从 0 开始计数),将tmp的二进制向右移动diff位,让目标位移动到最低位; - 再与 1 进行按位与运算,若结果为 1,说明当前
diff对应的位就是tmp中"最低为 1 的位"(记为第diff位)。
找到这一位后,它就成了拆分数字的"天然依据":
由于 tmp = a ^ b,且第 diff 位为 1,根据异或规则,a 和 b 在这一位的取值必然不同 ------一个是 0,另一个是 1。
基于此,我们可以将所有数字(包括数组 nums 中的元素和 [1, n] 范围内的完整数字)拆分为两组:
- 第一组:第
diff位为 1 的数字(包含其中一个缺失数,假设为a)与diff位为1的其他数*2 - 第二组:第
diff位为 0 的数字(包含另一个缺失数,假设为b)与diff位为0的其他数*2
这样的拆分能确保 a 和 b 被精准分到不同组中,而其他数字会因二进制位固定,成对出现在同一组里------为后续通过异或分离出缺失数做好了关键铺垫。
如下图所示👇:

3. 对拆分后的两个集合分别异或,得到两个缺失数。
我们上一步已经分好组,这样的分组会产生一个关键效果:即可以将a,b分开进行处理。
对于除 a 和 b 之外的其他数字(既存在于数组 nums 中,也属于 [1, n] 范围),它们会在两个关联集合(数组元素和 [1, n] 区间的所有数)中各出现一次,且必然被分到同一组中(因为同一个数字的二进制位是固定的),而 a 和 b 则会被严格分离到两个不同的组中。
我们就可以将两组分开异或运算,每组中就只剩下一个"只出现一次"的数字(即 a 或 b),其余数字都会因为出现两次而在异或运算中相互抵消------这就将"找两个缺失数"的问题,简化为"在两个独立分组中各找一个缺失数"的基础问题。
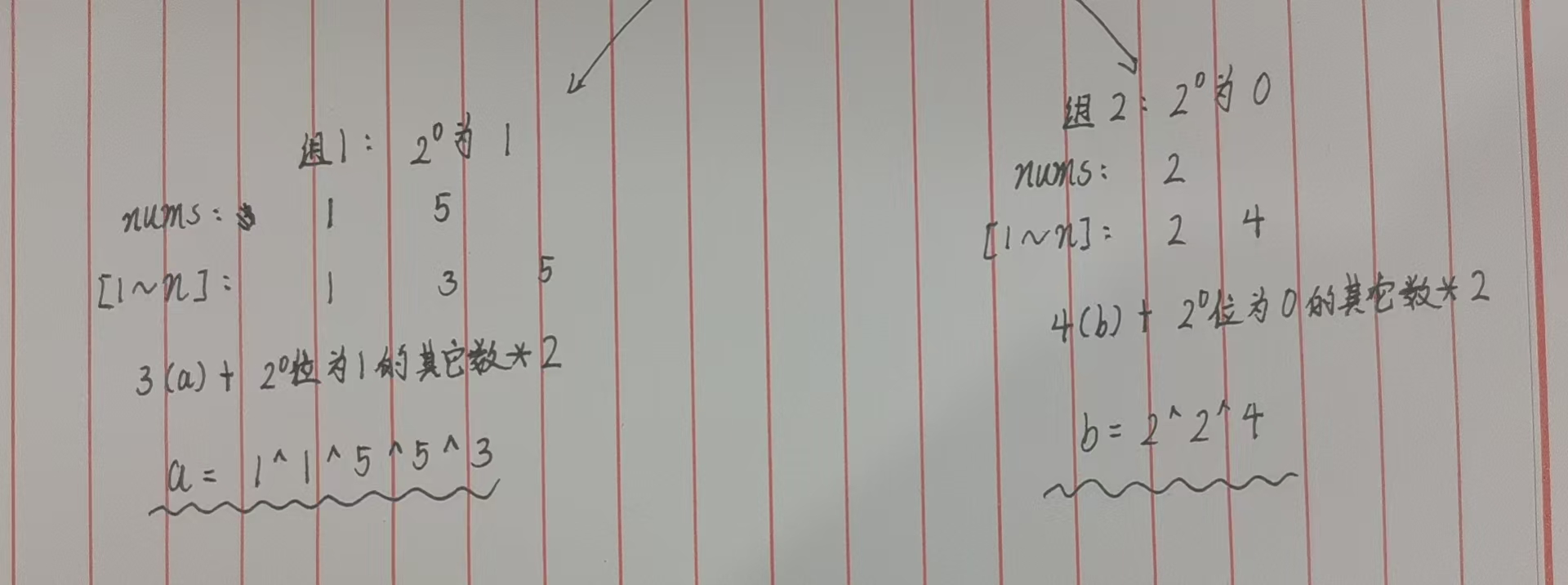
代码实现
基础实现
cpp
class Solution {
public:
vector<int> missingTwo(vector<int>& nums) {
// 步骤1:计算"两个缺失数的异或结果"
int tmp = 0;
// 异或数组中所有元素
for(auto x : nums) tmp ^= x;
// 异或1~(n)(n = 数组长度+2)
for(int i = 1; i <= nums.size() + 2; i++) tmp ^= i;
// 步骤2:找到异或结果中"最低为1的位"(diff是该位的掩码)
int diff = 0;
while(1)
{
// 检查tmp的第diff位是否为1
if(((tmp >> diff) & 1) == 1) break;
else diff++;
}
// 步骤3:按"第diff位是否为1"拆分集合,分别异或找缺失数
int a = 0, b = 0;
// 先异或数组中的元素
for(int x : nums)
if(((x >> diff) & 1) == 1) b ^= x; // 第diff位为1的元素归为一组
else a ^= x; // 第diff位为0的元素归为另一组
// 再异或1~n的元素
for(int i = 1; i <= nums.size() + 2; i++)
if(((i >> diff) & 1) == 1) b ^= i;
else a ^= i;
return {a, b};
}
};简单优化(sum & (-sum) 找最低有效位)
cpp
class Solution {
public:
vector<int> missingTwo(vector<int>& nums) {
// 步骤1:同上,计算两个缺失数的异或结果(变量名改为sum,不影响逻辑)
int sum = 0;
for(auto e : nums) sum ^= e;
for(int i = 1; i <= nums.size() + 2; i++) sum ^= i;
// 步骤2:优化!用sum & (-sum)直接获取"最低为1的位的掩码"
int mark = sum & (-sum);
// 步骤3:同上,按mark拆分集合并异或
int a = 0, b = 0;
for(auto e : nums)
if(mark & e) a ^= e; // 简化判断:mark的唯一1位与e的对应位进行与运算
else b ^= e;
for(int i = 1; i <= nums.size() + 2; i++)
if(mark & i) a ^= i;
else b ^= i;
return {a, b};
}
};代码优化说明
两个代码的核心算法思路完全一致 ,均基于我们上面的算法思路 与 "异或运算"的特性(x^x=0、x^0=x) 相同。
两者的差异仅在于第2步"找最低有效位"的实现方式,优化版通过数学技巧简化了代码、提升了效率,具体对比如下:
1. 基础版的实现逻辑(循环判断)
基础版通过while循环逐位检查tmp的每一位,直到找到"值为1的最低位":
cpp
int diff = 0;
while(1)
{
// 检查tmp的第diff位是否为1:将tmp右移diff位后,与1做"与运算"
if(((tmp >> diff) & 1) == 1) break;
else diff++; // 若当前位为0,diff+1,检查下一位
}缺点 :最坏情况下需要循环32次(int类型共32位),代码稍显冗余。
2. 优化版的实现逻辑
优化版直接使用sum & (-sum)这一数学公式,一步得到"最低有效位的掩码",无需循环:
cpp
int mark = sum & (-sum);核心原理 :基于计算机中"补码"的存储规则(负数用"原码取反+1"表示):
以sum=6(二进制000...000110)为例:
(1)-sum(即-6)的补码为:111...111010(对6的原码取反后加1);
(2) sum & (-sum):000...000110 & 111...111010 = 000...000010(仅保留"最低位为1"的位,其余为0)。
最终mark=2(二进制10),恰好对应"最低有效位的掩码",与基础版的(1 << diff)(当diff=1时,1<<1=2)效果完全一致。
优势:
- 代码简化:用1行代码替代循环,可读性更高;
- 效率提升:无需逐位判断,直接通过一次位运算得到结果,时间复杂度从
O(32)降为O(1)。
3. 优化后的连锁简化(分组判断)
由于优化版得到的mark是"最低有效位的掩码"(仅某一位为1,其余为0),分组判断也可以简化:
-
基础版需要通过
(x >> diff) & 1判断"第diff位是否为1"; -
优化版直接用
mark & x判断:若结果非0,说明x的"该位为1";若结果为0,说明"该位为0":cpp// 优化版分组逻辑(更简洁) if(mark & e) a ^= e; // 等价于基础版的"((e >> diff) & 1) == 1" else b ^= e; // 等价于基础版的"((e >> diff) & 1) == 0"
优化点汇总
| 对比维度 | 基础版 | 优化版 | 优化核心 |
|---|---|---|---|
| 找最低有效位 | 循环diff从0到31,逐位检查 |
1行代码sum & (-sum) |
利用补码特性,一步得掩码 |
| 时间效率 | 最坏O(32)(可视为O(1)) |
严格O(1) |
减少位运算次数 |
| 分组判断逻辑 | 需要右移+与运算,逻辑稍复杂 | 直接与mark做与运算,逻辑直观 |
复用掩码,简化条件判断 |
其他解法优劣势对比
| 解法 | 时间复杂度 | 空间复杂度 | 优势 | 劣势 |
|---|---|---|---|---|
| 位运算解法(我们所用的方法) | O(n) | O(1) | ✅ 空间最优:仅用几个变量,无额外空间开销 ✅ 效率稳定:遍历次数固定为2次n,无波动 ✅ 无数据范围限制:无需担心哈希表的扩容或数组越界 | ⚠️ 逻辑依赖位运算基础:需理解异或特性和补码规则,对新手不友好 |
| 哈希表暴力法 | O(n) | O(n) | ✅ 逻辑直观:易理解,编码难度低 | ❌ 空间开销大:需要存储n-2个元素,不符合"常数空间"要求 ❌ 效率受哈希表影响:极端情况下哈希表查找可能退化为O(n) |
| 数组标记法 | O(n) | O(n) | ✅ 逻辑简单:用数组下标对应数字,标记出现状态 | ❌ 空间开销大:需创建长度为n的数组 ❌ 受n范围限制:n过大时数组会占用大量内存 |
面试避坑指南
- 拆分集合时漏异或"1~n" :步骤3必须同时异或"数组元素"和"1~n的元素",只异或其一会导致结果错误(因为需要抵消重复出现的数);
- 找最低位时循环条件错误 :第一版代码中,
diff从0开始递增,判断条件是((tmp >> diff) & 1) == 1,不要写成((tmp & (1 << diff)) == 0)(逻辑颠倒); - 忽略"补码"导致
sum & (-sum)用错 :仅当sum为非负数时该技巧有效,但本题中sum是异或结果,必然非负(异或不产生负数),无需额外处理; - 返回结果顺序错误 :题目不要求缺失数按大小排序,返回
{a,b}或{b,a}均正确,但面试中可主动说明"若需排序可加一句if(a > b) swap(a,b)",体现细节考虑。
总结
位运算类题目侧重于利用二进制数的特性和位操作技巧(如异或、与、或、位移等)解决问题,其核心在于:
- 挖掘问题与二进制表示的内在联系
- 运用数学性质简化计算(如
x^x=0、sum&(-sum)找最低有效位等) - 追求极致的时间和空间效率优化
- 思维方式偏向数学推导和技巧应用
我们的位运算到这里就告一段落了,接下来我们一起讨论 力扣1576 替换所有的问号,我们一起学习如何通过模拟的思路,按照题目要求一步步处理字符串中的每个问号,确保最终结果满足相邻字符不同的约束条件。
如果这篇内容对你有帮助,别忘了 点赞👍 + 收藏⭐ + 关注👀 哦!
有问题欢迎在评论区留言,我会认真思考并及时回复!