1.最长公共前缀
题目链接:14. 最长公共前缀 - 力扣(LeetCode)

题目解析:返回最长公共前缀
算法讲解:
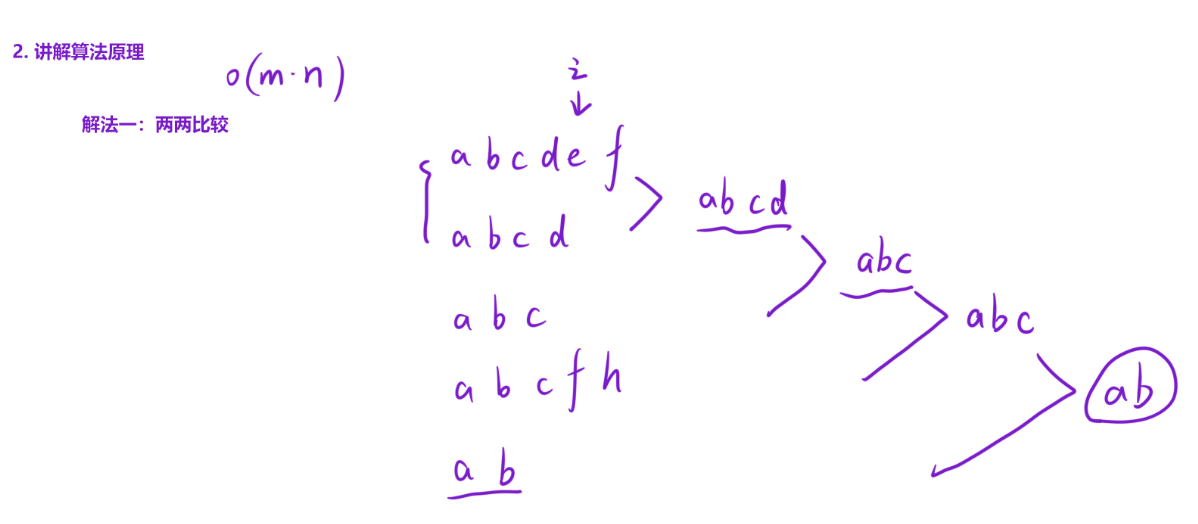
解法一:两两比较
先将第一个字符串和第二个字符串的最长公共前缀获取到,假设这个最长前缀为str,然后再拿这个str和第三个字符串比较,知道将所有字符串都两两比较一遍
此时代码的核心就变成了提取两个字符串的最长公共前缀
提取两个字符串的最长公共前缀的思路:当两个字符串对应的字符相同且i在两个字符串之间不越界的情况下,让i++即可
时间复杂度分析:
假设字符串的平均长度为m,假设有n个字符串,此时最坏的情况下字符串中的每个字符都要比较,则此时时间复杂度为O(N)
代码实现:
java
class Solution {
public String longestCommonPrefix(String[] strs) {
String ret=strs[0];
for(int i=1;i<strs.length;i++){
ret=findCommon(ret,strs[i]);
}
return ret;
}
public String findCommon(String ret,String str){
int i=0;
while(i<Math.min(ret.length(),str.length()) && ret.charAt(i)==str.charAt(i)){
i++;
}
return ret.substring(0,i);
}
}解法二:统一比较
统一比较就是一个字符一个字符一次比较,假设先去判断第一个字符时,就去所有的字符串里面比较,看所有的字符串是否有这个第一个字符,r如果有就去判断第二个字符,第二字符的比较也是以此类推,如果让i一直顺利的走到最后,说明所有的字符串都是相同的字符串,此时直接返回任意一个字符串即可
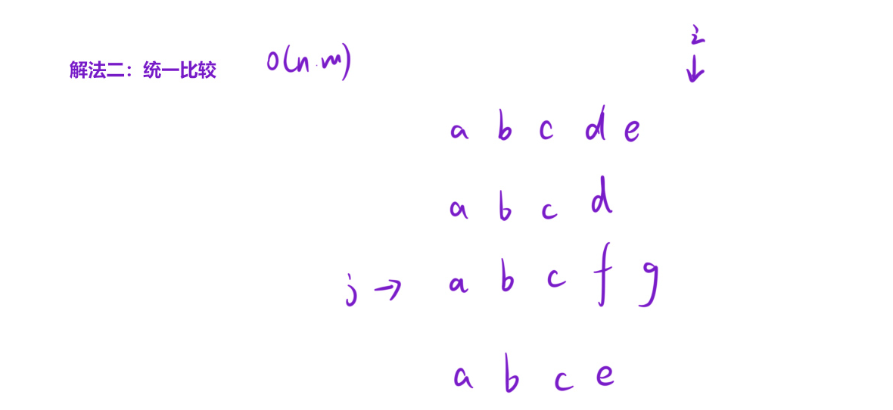
代码实现:
java
class Solution {
public String longestCommonPrefix(String[] strs) {
String str=strs[0];
for(int i=0;i<str.length();i++){
char tmp=str.charAt(i);
for(int j=1;j<strs.length;j++){
String s=strs[j];
if(i==s.length() || s.charAt(i) != tmp){
return str.substring(0,i);
}
}
}
return str;
}
}2.最长回文子串
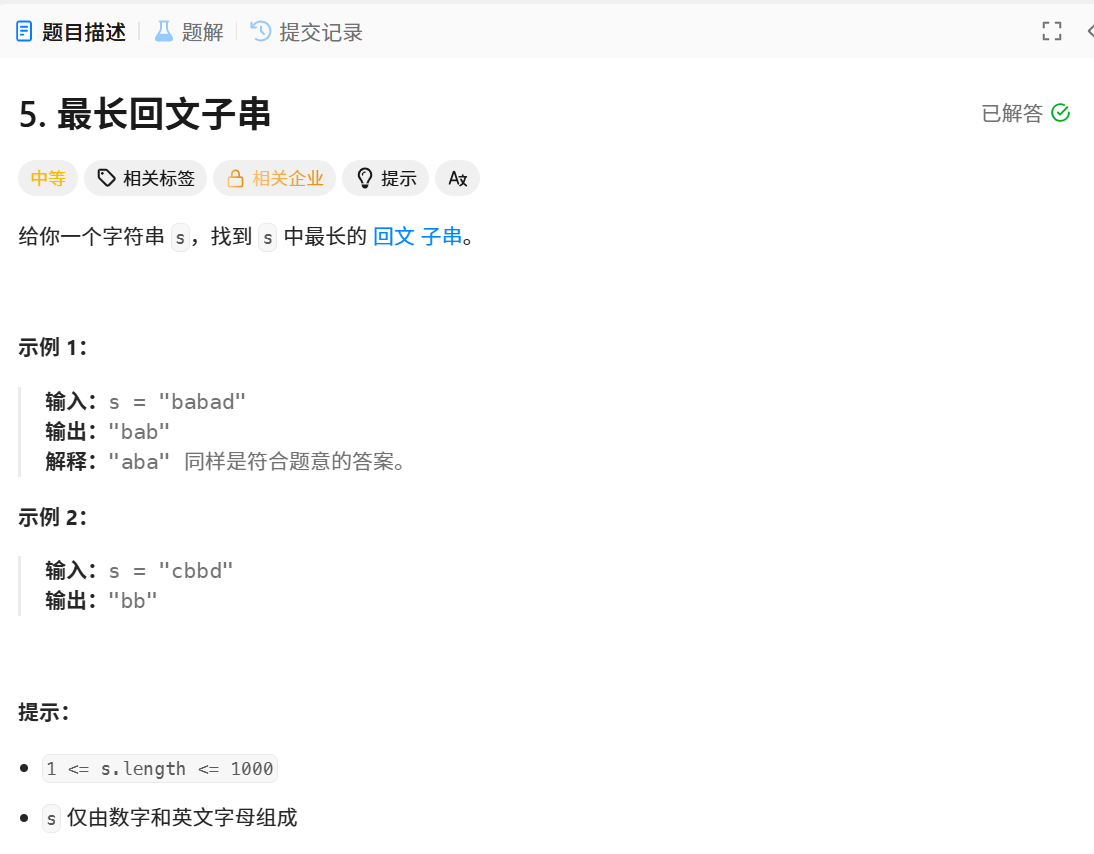
题目解析:返回字符串s中的最长回文子串
算法讲解:中心扩展算法
遍历字符串s,每次都已遍历到的字符串为中心,定义两个指针left和right,一开始都让他们指向中心,如果s[left]==s[right]且left和right都没越界,此时就让left和right越界或者s[left]!=s[right]
但是以上面的那种方案,只考虑了回文子串的长度为奇数的情况,没有考虑到回文子串长度为偶数的情况,如果考虑偶数的情况下,一开始只要让right在中心的下一个位置或者让left处于中心位置的前一个位置
因为题目要求的是回文子串,无论回文子串长度是偶数还是奇数,最终left指向的位置就是恰好不为回文子串的位置,所以left-1就是为最长回文子串的开始位置
代码实现:
java
class Solution {
public String longestPalindrome(String _s) {
char[] s = _s.toCharArray();
int start=0;
int n=s.length;
int maxLength=1;
for(int i=0;i<n;i++){
int left=i;
int right=i;
//奇数
while(left>=0&&right<n&&s[left]==s[right]){
left--;
right++;
}
if(maxLength<right-left-1){
maxLength=right-left-1;
start=left+1;
}
//偶数
left=i;
right=i+1;
while(left>=0&&right<n&&s[left]==s[right]){
left--;
right++;
}
if(maxLength<right-left-1){
maxLength=right-left-1;
start=left+1;
}
}
return _s.substring(start,start+maxLength);
}
}3.二进制求和
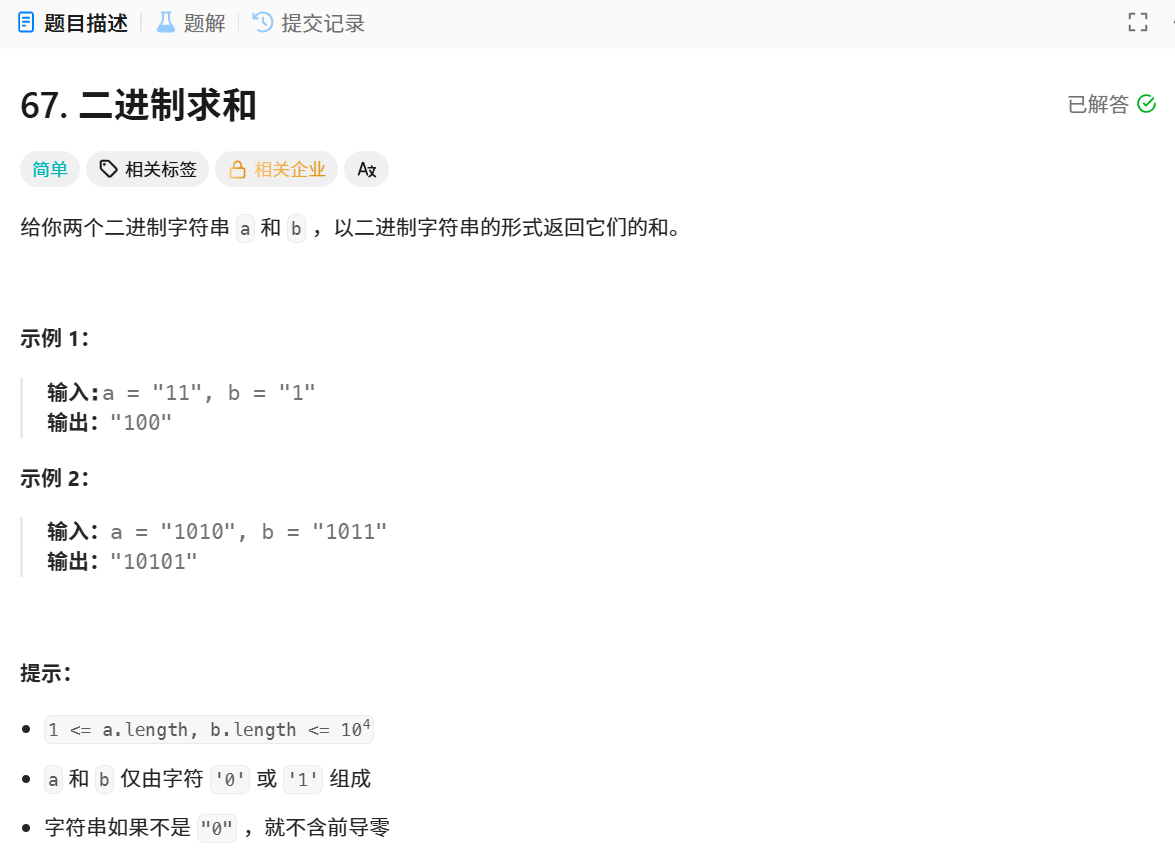
算法讲解:模拟列竖式运算
由于列竖式运算是从后往前计算,所以我们从后往前遍历字符串a和字符串b,将每次遍历到的数字提取出来,创建一个变量t来记录进位情况,此时还要创建一个字符串ret来记录每一位相加的结果,每次让ret.appned(t%2),t%2是因为只需要相加结果的个为即可
一个小细节:遍历字符串a和字符串b时,有可能会出现越界的情况,此时只要将越界的字符串对应的数字弄为0即可
有ret.append一直是尾插,所以最终返回时要先对ret逆序一下再返回
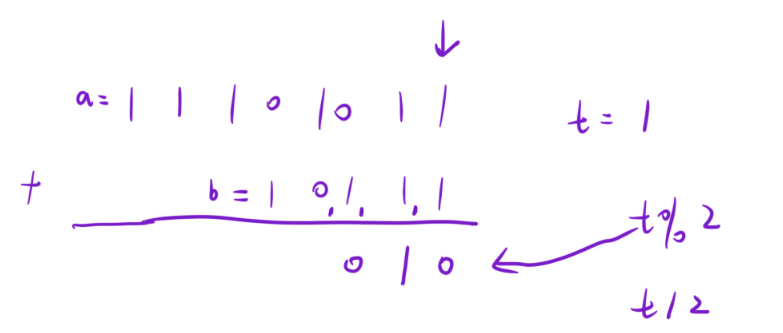
代码实现:
java
class Solution {
public String addBinary(String a, String b) {
int lenA=a.length();
int lenB=b.length();
int aa=0;
int bb=0;
int t=0;
StringBuffer ret = new StringBuffer();
while(lenA-1>=0 || lenB-1>=0 || t!=0){
if(lenA-1<0){
aa=0;
}else{
aa=a.charAt(lenA-1)-'0';
}
if(lenB-1<0){
bb=0;
}else{
bb=b.charAt(lenB-1)-'0';
}
t+=aa;
t+=bb;
ret.append(t%2);
t/=2;
lenA--;
lenB--;
}
return ret.reverse().toString();
}
}4.字符串相乘
算法讲解:先无进位相乘,最后再处理进位
首先对两个字符串进行逆序处理,然后进行相乘。
相乘的时候,假设m为num1的长度,n为num2的长度,创建一个空间大小为[m+n-1]的数组tmp,tmp用来存储每一位相乘的结果,此时tmp中记录的结果恰好可以对应到逆序后的num1和逆序后的num2每一位相乘的结果
什么意思呢?
tmp[0]中记录就是逆序后num1和num2中第0个数字字符相乘的结果,tmp[1]就是num1[1]*num2[0]+num1[0]*num2[1]的结果,然后以此类推下去
处理完无进位相乘后,此时再按照两数相加的做法去处理tmp
最后再处理一下前导0的情况即可
java
class Solution {
public String multiply(String num1, String num2) {
int len1=num1.length();
int len2=num2.length();
int[] tmp = new int[len1+len2-1];
StringBuffer ret = new StringBuffer();
//逆序
String s1=new StringBuffer(num1).reverse().toString();
String s2=new StringBuffer(num2).reverse().toString();
//无进位相乘
for(int i=0;i<s1.length();i++){
int first = s1.charAt(i)-'0';
for(int j=0;j<s2.length();j++){
int second = s2.charAt(j)-'0';
int sum=first*second;
tmp[i+j]+=sum;
}
}
//处理进位
int t=0;
for(int i=0;i<tmp.length;i++){
t+=tmp[i];
ret.append(t%10);
t/=10;
}
if(t!=0) ret.append(t);
//处理前导0
while(ret.length()>1&&ret.charAt(ret.length()-1)=='0'){
ret.deleteCharAt(ret.length()-1);
}
return ret.reverse().toString();
}
}