LeetCode算法日记 - Day 64: 岛屿的最大面积、被围绕的区域

[1. 岛屿的最大面积](#1. 岛屿的最大面积)

[1.1 题目解析](#1.1 题目解析)

[1.2 解法](#1.2 解法)

[1.3 代码实现](#1.3 代码实现)

[2. 被围绕的区域](#2. 被围绕的区域)

[2.1 题目解析](#2.1 题目解析)

[2.2 解法](#2.2 解法)

[2.3 代码实现](#2.3 代码实现)

1. 岛屿的最大面积

https://leetcode.cn/problems/max-area-of-island/

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例 1：

复制代码

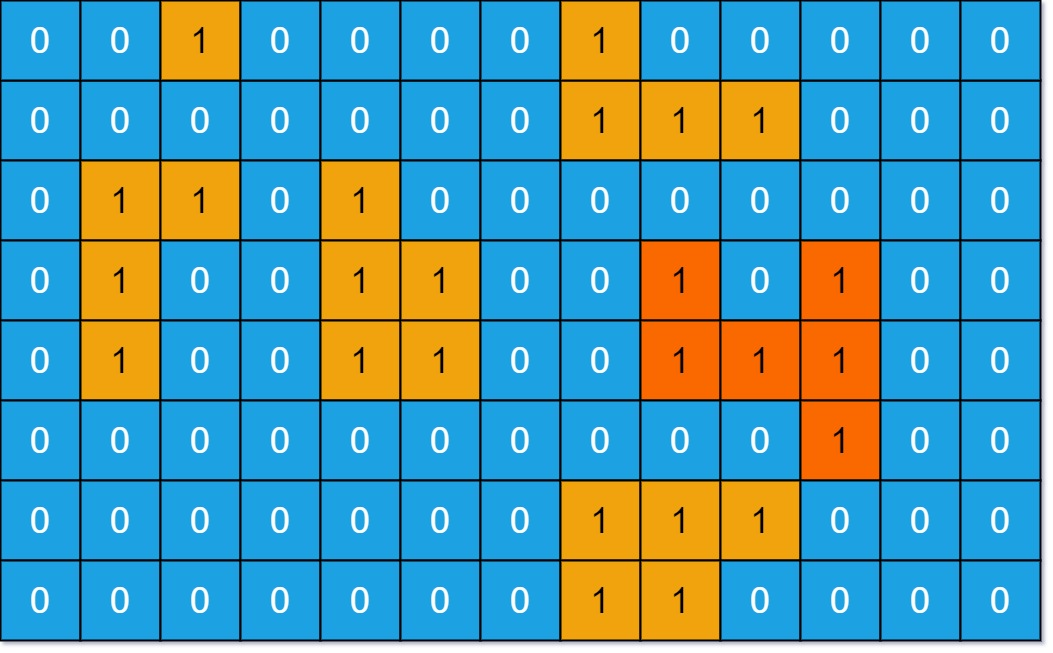
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：

复制代码

输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 50
grid[i][j] 为 0 或 1

1.1 题目解析

题目本质

这是一道经典的「连通分量统计」问题，核心是在二维网格中找出所有由 1 组成的连通区域，并返回最大连通区域的面积。

常规解法

遍历矩阵，遇到未访问的 1 就开始搜索，统计这块岛屿的面积，最后返回所有岛屿中的最大值。

问题分析

直观解法就是正解，关键在于选择合适的搜索方式。可以用 DFS（深度优先搜索）或 BFS（广度优先搜索），两者时间复杂度相同，只是实现方式不同：

DFS 用递归，代码简洁但可能栈溢出

BFS 用队列，需要额外空间但更安全

思路转折

要想避免重复统计 → 必须标记已访问节点 → 使用 vis 数组。要想统计完整岛屿 → 必须遍历所有相邻的 1 → 四个方向递归/迭代搜索。

1.2 解法

算法思想

使用 DFS（深度优先搜索）遍历每个岛屿，统计岛屿面积
维护 vis 数组标记已访问节点，避免重复计算
递推逻辑：当前岛屿面积 = 1（当前节点）+ 四个方向未访问邻居的岛屿面积之和
公式：area = 1 + ∑ area(neighbor)，其中 neighbor 是四个方向上满足条件的邻居

**i）初始化：**记录矩阵大小 m×n，创建 vis 数组标记访问状态

**ii）双层遍历：**遍历矩阵每个位置 (i,j)

**iii）触发搜索：**若 grid[i][j] == 1 且未访问，则从该点开始 DFS 搜索

iv）DFS 递归：

标记当前节点为已访问

面积计数器 +1

向四个方向递归搜索未访问的 1

返回累计面积

**v）更新答案：**每次 DFS 返回后，用返回值更新最大面积

**vi）返回结果：**遍历结束后返回最大岛屿面积

易错点

**提前标记：**必须在递归调用前标记 vis[x][y] = true，否则同一节点可能被重复访问导致死循环或计数错误

**全局变量陷阱：**使用全局变量 cur 统计面积时，每次新岛屿搜索前必须重置为 0，否则会累加到之前的岛屿面积

**边界检查顺序：**必须先检查边界 x>=0 && x<m && y>=0 && y<n，再访问 grid[x][y]，否则可能数组越界

1.3 代码实现

java 复制代码

class Solution {
    int m, n;
    boolean[][] vis;
    int[] dx = {0, 0, 1, -1};
    int[] dy = {1, -1, 0, 0};
    int cur;  // 当前岛屿面积
    
    public int maxAreaOfIsland(int[][] grid) {
        m = grid.length;
        if (m == 0) return 0;
        n = grid[0].length;
        vis = new boolean[m][n];
        
        int maxArea = 0;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 1 && !vis[i][j]) {
                    cur = 0;  // 重置计数器
                    int area = dfs(grid, i, j);
                    maxArea = Math.max(maxArea, area);
                }
            }
        }
        return maxArea;
    }
    
    private int dfs(int[][] grid, int x, int y) {
        vis[x][y] = true;
        cur++;  // 统计当前节点
        
        // 四个方向递归
        for (int i = 0; i < 4; i++) {
            int nx = x + dx[i];
            int ny = y + dy[i];
            if (nx >= 0 && nx < m && ny >= 0 && ny < n 
                && grid[nx][ny] == 1 && !vis[nx][ny]) {
                vis[nx][ny] = true;  // 提前标记
                dfs(grid, nx, ny);
            }
        }
        return cur;
    }
}

复杂度分析

时间复杂度：O(m × n)，每个节点最多访问一次

空间复杂度：O(m × n)，vis 数组占用 O(m × n) 空间，递归栈最坏情况（整个矩阵都是 1）占用 O(m × n) 空间

2. 被围绕的区域

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' 组成，捕获所有 被围绕的区域：

**连接：**一个单元格与水平或垂直方向上相邻的单元格连接。
区域：连接所有 'O' 的单元格来形成一个区域。
围绕： 如果您可以用 'X' 单元格 连接这个区域 ，并且区域中没有任何单元格位于 board 边缘，则该区域被 'X' 单元格围绕。

通过原地将输入矩阵中的所有 'O' 替换为 'X' 来 捕获被围绕的区域。你不需要返回任何值。

示例 1：

**输入：**board = [['X','X','X','X'],['X','O','O','X'],['X','X','O','X'],['X','O','X','X']]

输出：[['X','X','X','X'],['X','X','X','X'],['X','X','X','X'],['X','O','X','X']]

解释：

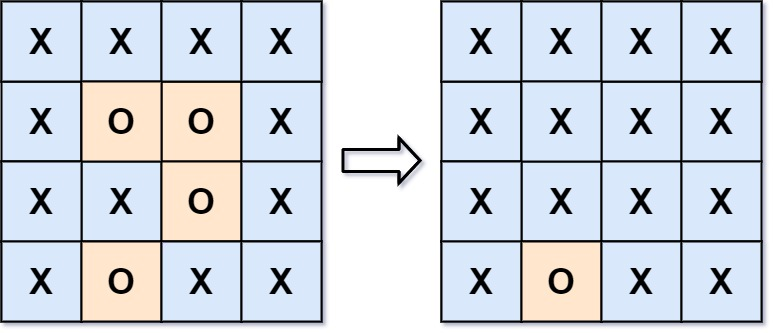
在上图中，底部的区域没有被捕获，因为它在 board 的边缘并且不能被围绕。

示例 2：

**输入：**board = [['X']]

输出：[['X']]

提示：

m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j] 为 'X' 或 'O'

2.1 题目解析

题目本质

这是一道「反向标记连通分量」问题，核心是区分哪些 'O' 区域是被完全围绕的（内部），哪些是连通到边界的（外部）。

常规解法

遍历矩阵内部的每个 'O'，对其进行 DFS/BFS 搜索，检查这个连通区域是否能到达边界。如果不能到达边界，就把整个区域标记为 'X'。

问题分析

这种"逐个检查是否到边界"的做法存在大量重复搜索。同一个连通区域内的每个 'O' 都会触发一次搜索，时间复杂度可能达到 O((m×n)²)。当矩阵较大且 'O' 较多时，效率极低。

思路转折

要想避免重复搜索 → 必须换个角度思考 → 反向标记。关键洞察：不被围绕的 'O' 一定连通到边界 → 从边界出发标记所有连通的 'O' → 剩下未标记的 'O' 就是被围绕的 → 直接替换为 'X'。这样每个节点只访问一次，时间复杂度降到 O(m×n)。

2.2 解法

算法思想

使用反向标记 + DFS/BFS 的策略：先保护边界连通的 'O'，再消灭内部的 'O'
三步走：
- 标记阶段：从四条边出发，把所有连通的 'O' 临时标记为 'A'（表示安全区域）
- 替换阶段：遍历矩阵，将剩余的 'O'（被围绕的）改为 'X'，将 'A' 还原为 'O'
核心逻辑：安全区域 = 从边界可达的 'O'，被围绕区域 = 所有 'O' - 安全区域

**i）边界检查：**处理空矩阵边界情况，初始化矩阵大小 m×n

ii）第一轮标记 （保护边界连通区域）：

遍历上下两条边的每一列，若为 'O' 则 DFS 标记为 'A'
遍历左右两条边的每一行（跳过四个角避免重复），若为 'O' 则 DFS 标记为 'A'

iii）DFS 递归标记：

将当前 'O' 改为 'A'
向四个方向递归，继续标记相邻的 'O'

iv）第二轮替换（处理结果）：

遍历整个矩阵
遇到 'O' → 改为 'X'（被围绕的区域）
遇到 'A' → 改为 'O'（恢复边界连通区域）

**v）原地修改：**直接在原矩阵上操作，无需返回值

易错点

**边界遍历重复：**遍历左右两条边时，要从 i=1 到 i=m-2，避免重复处理四个角的位置（它们已经在上下边的遍历中处理过）

**标记时机错误：**必须在访问节点时立即标记为 'A'，不能先入队/递归再标记，否则同一节点可能被多次访问导致栈溢出或性能问题

**替换逻辑混乱：**第二轮遍历时，'O' 和 'A' 的处理不能搞反：'O' 是要消灭的（改为 'X'），'A' 是要保留的（还原为 'O'）

**临时标记冲突：**选择 'A' 作为临时标记是因为题目只有 'X' 和 'O'，若题目包含其他字符需要选择不冲突的标记

2.3 代码实现

java 复制代码

class Solution {
    int m, n;
    int[] dx = {0, 0, 1, -1};
    int[] dy = {1, -1, 0, 0};

    public void solve(char[][] board) {
        if (board == null || board.length == 0) return;
        m = board.length;
        n = board[0].length;

        // 1. 从四条边出发，标记所有连通的 'O' 为 'A'
        // 上下两条边
        for (int j = 0; j < n; j++) {
            if (board[0][j] == 'O') dfs(board, 0, j);
            if (board[m - 1][j] == 'O') dfs(board, m - 1, j);
        }
        // 左右两条边（跳过角落避免重复）
        for (int i = 1; i < m - 1; i++) {
            if (board[i][0] == 'O') dfs(board, i, 0);
            if (board[i][n - 1] == 'O') dfs(board, i, n - 1);
        }

        // 2. 遍历矩阵，'O' 改为 'X'，'A' 还原为 'O'
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (board[i][j] == 'O') {
                    board[i][j] = 'X';      // 被围绕的区域
                } else if (board[i][j] == 'A') {
                    board[i][j] = 'O';      // 边界连通区域
                }
            }
        }
    }

    // DFS：把从 (x, y) 出发连通的 'O' 标记为 'A'
    private void dfs(char[][] board, int x, int y) {
        board[x][y] = 'A';  // 立即标记
        
        for (int k = 0; k < 4; k++) {
            int nx = x + dx[k];
            int ny = y + dy[k];
            if (nx >= 0 && nx < m && ny >= 0 && ny < n && board[nx][ny] == 'O') {
                dfs(board, nx, ny);
            }
        }
    }
}

复杂度分析

**时间复杂度：O(m × n)，**每个节点最多访问一次（标记阶段一次 + 替换阶段一次）

**空间复杂度：DFS 版本：O(m × n)，**最坏情况递归栈深度（整个矩阵都是边界连通的 'O'）