聚类之KMeans

PKNLP2025-10-09 17:05

一、聚类算法简介

学习目标：

1.知道什么是聚类

2.了解聚类算法的应用场景

3.知道聚类算法的分类

聚类算法介绍

一种典型的无监督学习算法，主要用于将相似的样本自动归到一个类别中。

在聚类算法中根据样本之间的相似性，将样本划分到不同的类别中，对于不同的相似度计算方法，会得到不同的聚类结果，常用的相似度计算方法有欧式距离法。

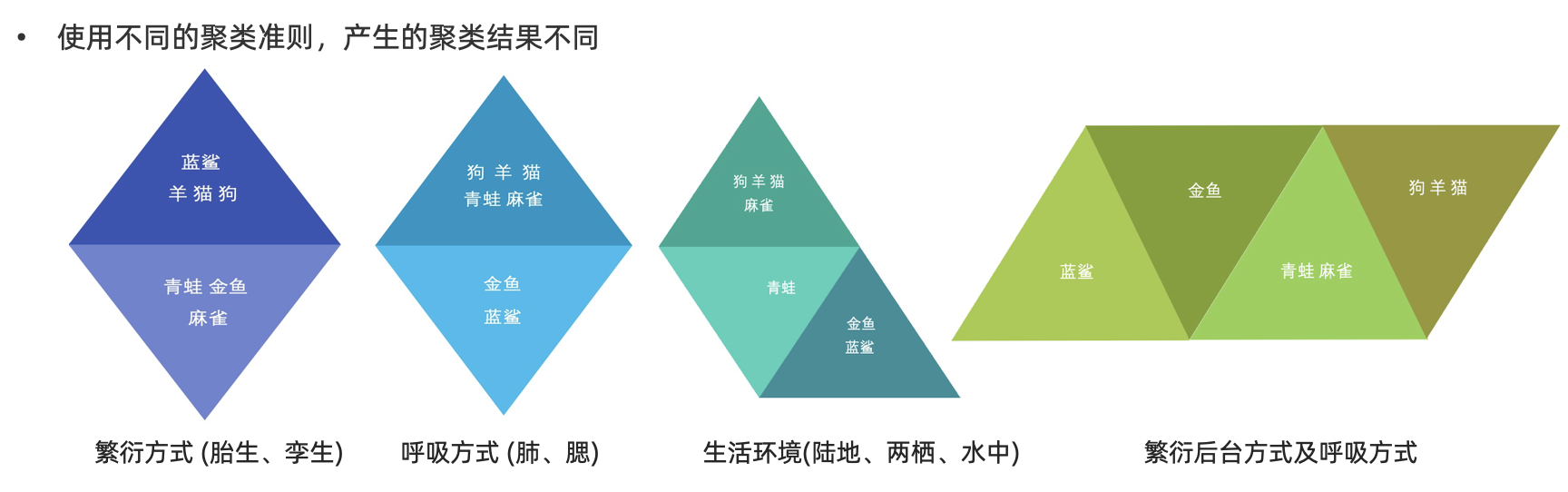
聚类算法在现实中的应用

  • 用户画像，广告推荐，Data Segmentation，搜索引擎的流量推荐，恶意流量识别
  • 基于位置信息的商业推送，新闻聚类，筛选排序
  • 图像分割，降维，识别；离群点检测；信用卡异常消费；发掘相同功能的基因片段

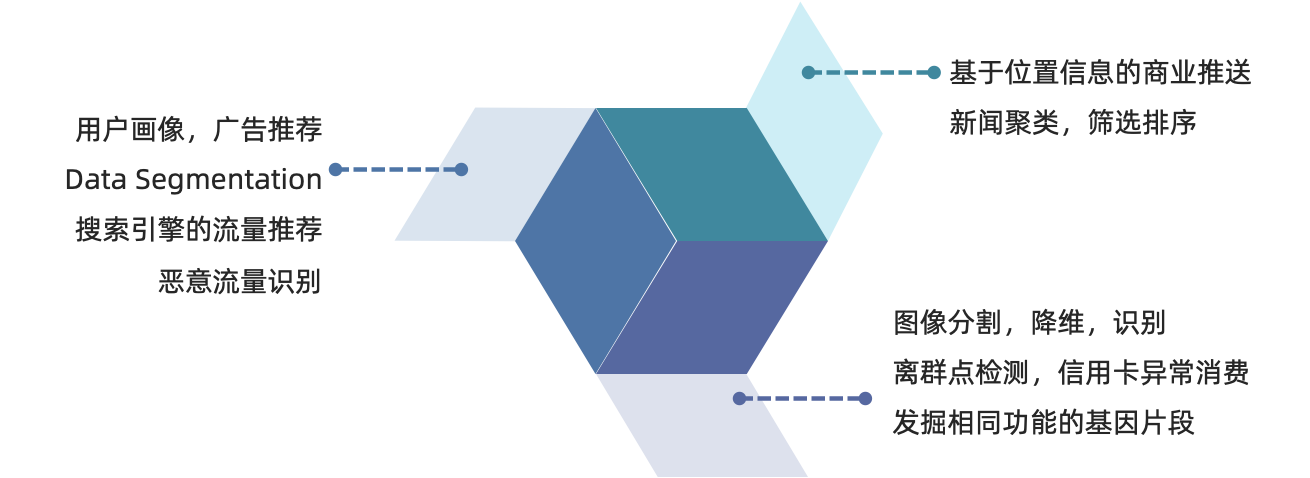
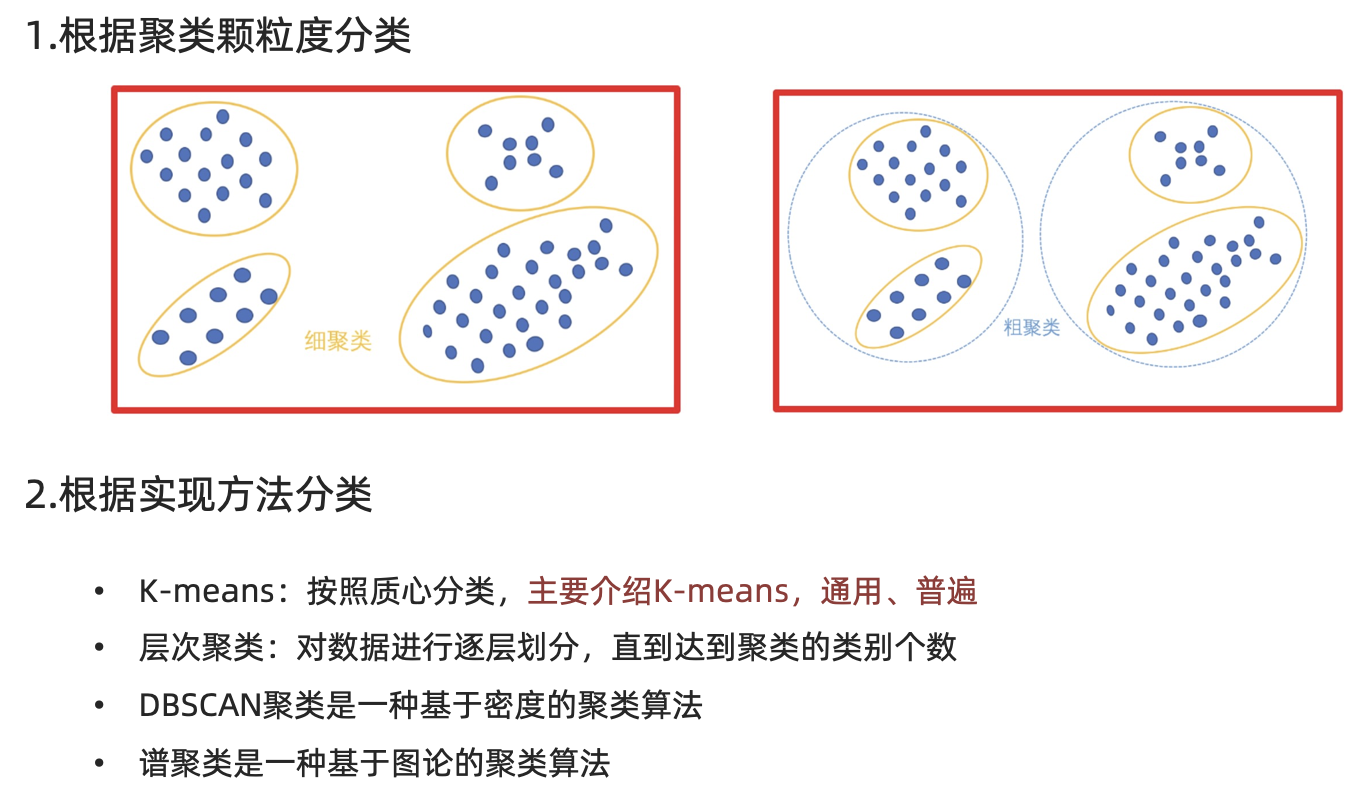
分类

二、Kmeans聚类API的初步使用

学习目标：

1.了解Kmeans算法的API

2.动手实践Kmeans算法

api介绍

  • sklearn.cluster.KMeans(n_clusters=8)
    • 参数:
      • n_clusters:开始的聚类中心数量
        • 整型，缺省值=8，生成的聚类数，即产生的质心（centroids）数。
    • 方法:
      • estimator.fit(x)
      • estimator.predict(x)
      • estimator.fit_predict(x)
        • 计算聚类中心并预测每个样本属于哪个类别,相当于先调用fit(x),然后再调用predict(x)

案例

随机创建不同二维数据集作为训练集，并结合k-means算法将其聚类，你可以尝试分别聚类不同数量的簇，并观察聚类效果：

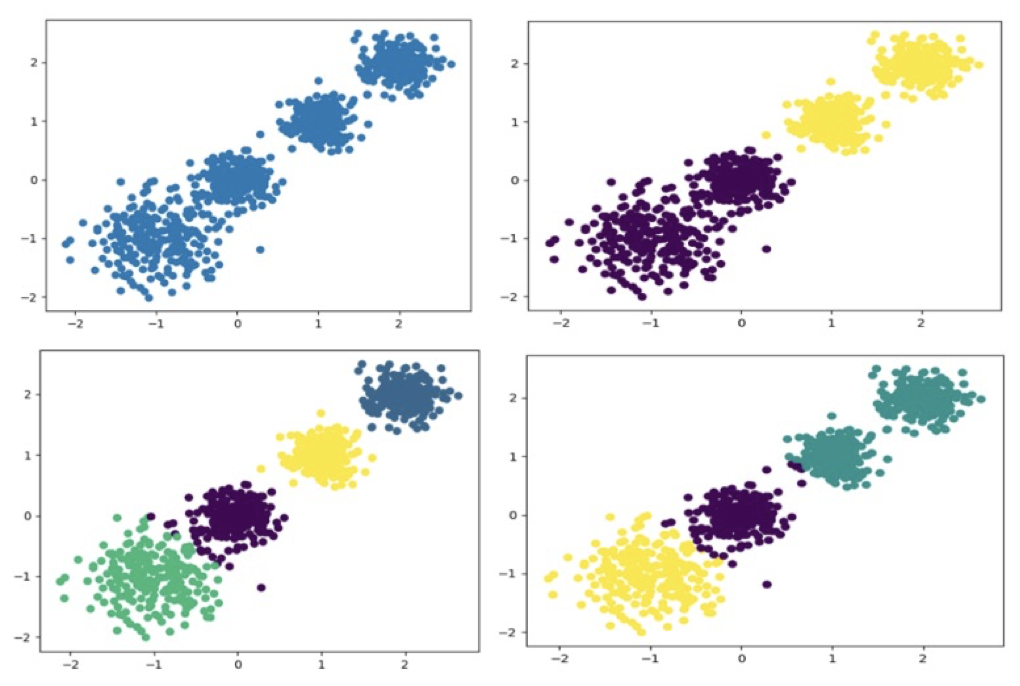
1.创建数据集

python 复制代码 
# -*- coding: utf-8 -*-
"""
任务需求：通过Kmeas算法对构造的数据集进行聚类
实现步骤：
    1.构造数据
    2.Kmeans实例化并聚类
    3.聚类结果展示
    4.聚类结果评价
"""
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn.metrics import calinski_harabasz_score
# 1.构造数据
x, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
                  cluster_std=[0.4, 0.2, 0.2, 0.2], random_state=22)
# print(x)
# print(y)
# plt.scatter(x[:, 0], x[:,1], c=y)
# plt.show()

# 2.Kmeans实例化并聚类
k_means = KMeans(n_clusters=4)
y_pred = k_means.fit_predict(x)

# 3.聚类结果展示
plt.scatter(x[:,0], x[:, 1], c=y_pred)
plt.show()

# 4.聚类结果评价
score = calinski_harabasz_score(x, y)
score_kmeans = calinski_harabasz_score(x, y_pred)
print(f"原始数据集的ch轮廓系数：{score}")
print(f"聚类结果的ch轮廓系数：{score_kmeans}")

三、Kmeans算法流程

学习目标

1、理解Kmeans算法的执行过程

k-means聚类流程

1、随机设置K个特征空间内的点作为初始的聚类中心

2、对于其他每个点计算到K个中心的距离，未知的点选择最近的一个聚类中心点作为标记类别

3、接着对着标记的聚类中心之后，重新计算出每个聚类的新中心点（平均值）

4、如果计算得出的新中心点与原中心点一样（质心不再移动），那么结束，否则重新进行第二步过程

通过下图解释实现流程：

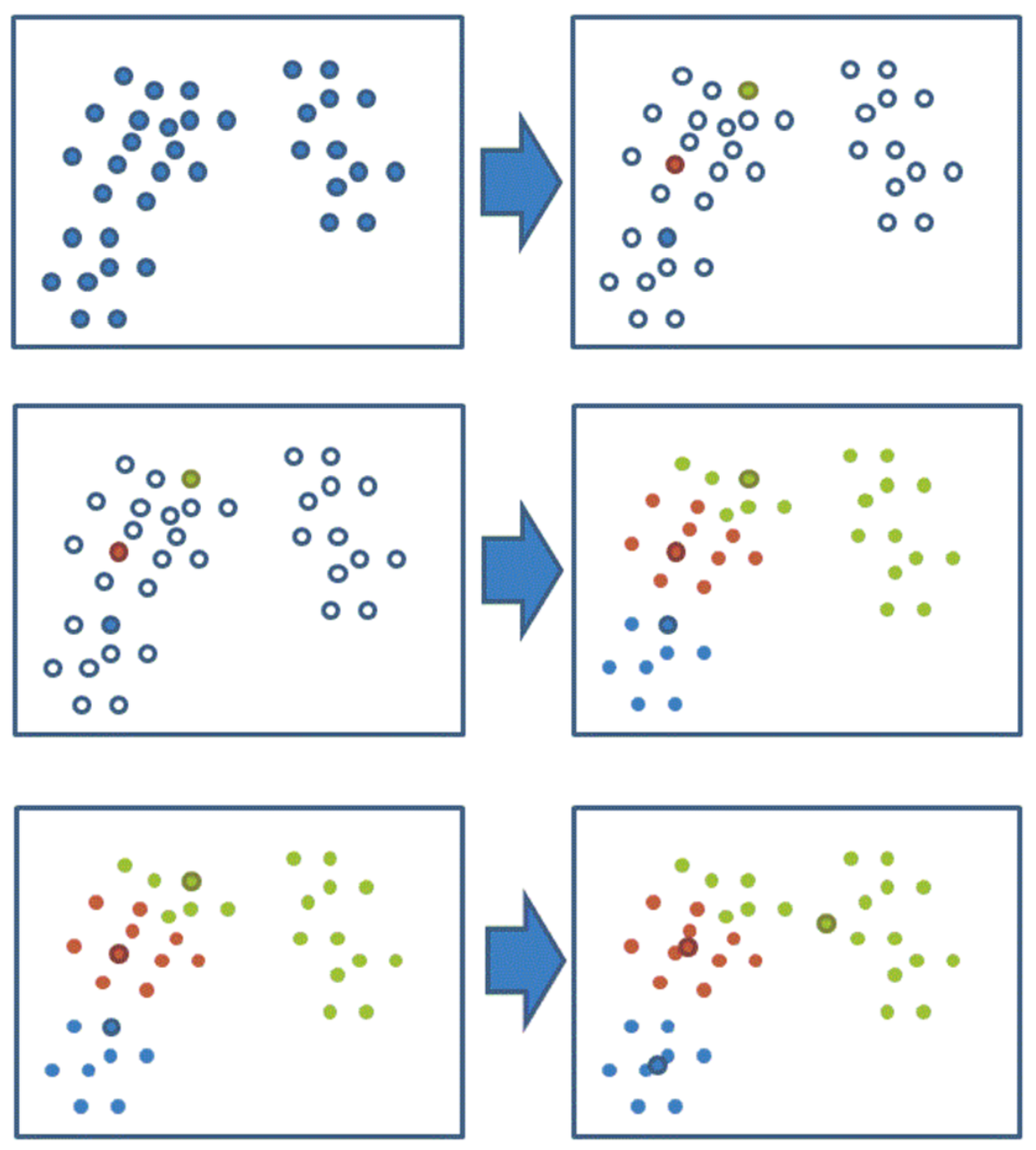
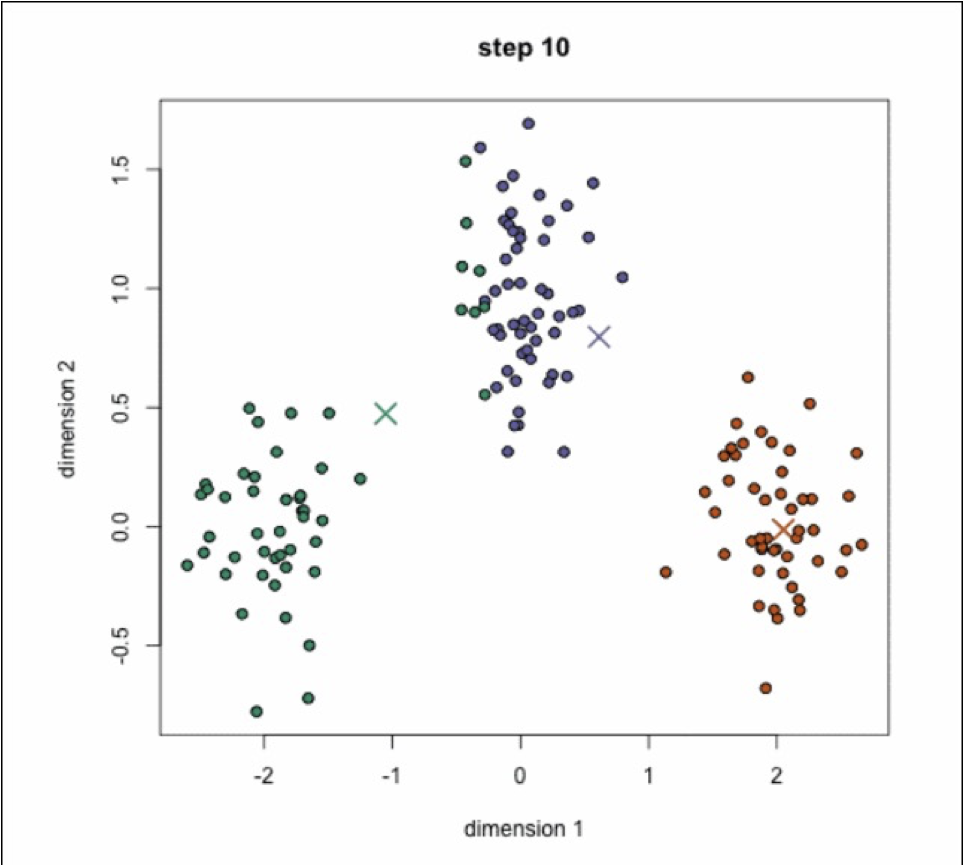
k-means聚类动态效果图：

四、评价指标

学习目标:

  1. 了解 SSE 聚类评估指标
  2. 了解 SC 聚类评估指标
  3. 了解 CH 聚类评估指标
  4. 了解肘方法的作用

SSE-误差平方和

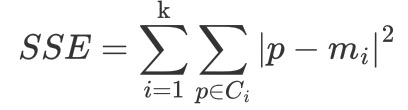
  1. K 表示聚类中心的个数

  2. Ci 表示簇

  3. p 表示样本

  4. mi 表示簇的质心

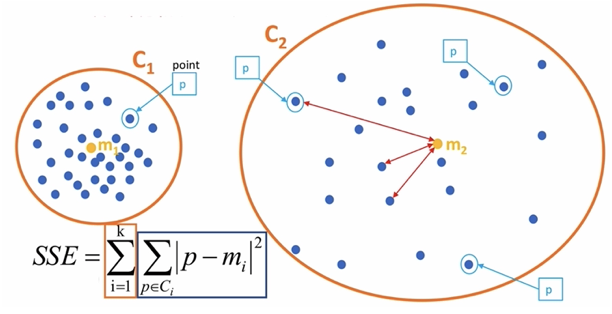
SSE 越小，表示数据点越接近它们的中心，聚类效果越好。

SC 系数

结合了聚类的凝聚度（Cohesion）和分离度（Separation），用于评估聚类的效果。

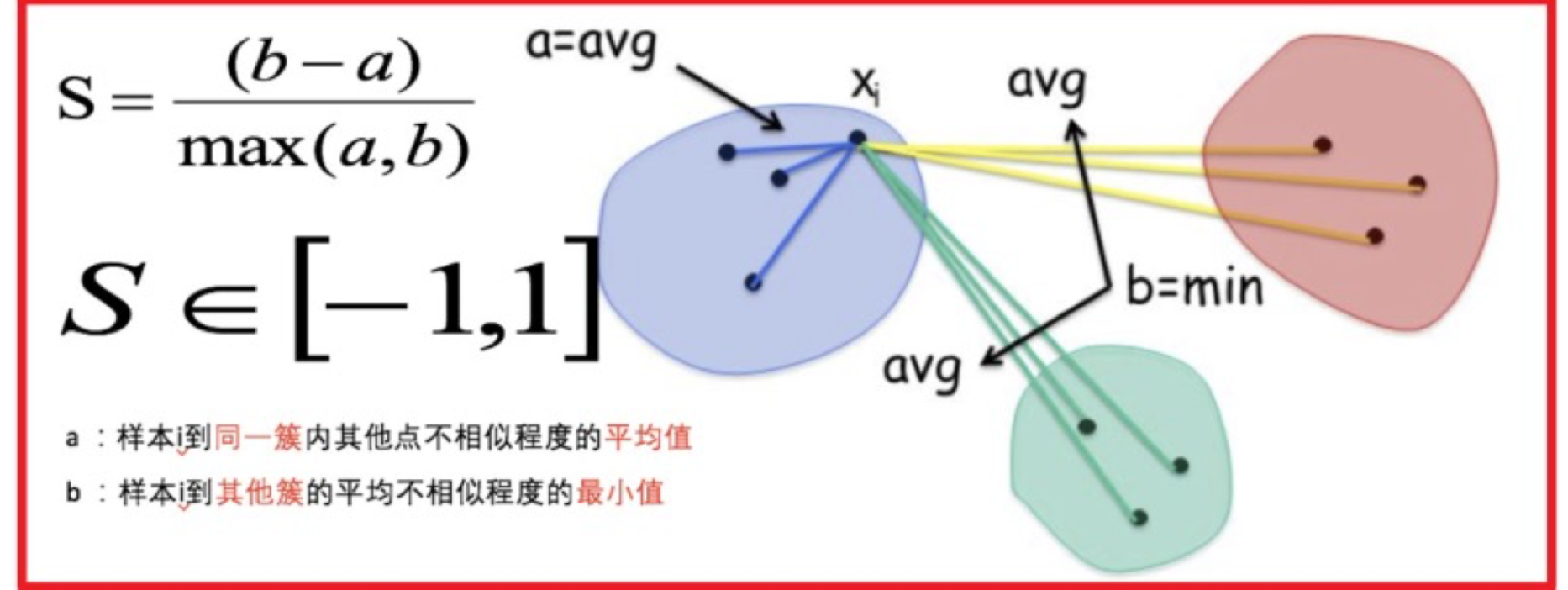
其计算过程如下：

  1. 计算每一个样本 i 到同簇内其他样本的平均距离 ai，该值越小，说明簇内的相似程度越大
  2. 计算每一个样本 i 到最近簇 j 内的所有样本的平均距离 bij，该值越大，说明该样本越不属于其他簇 j
  3. 计算所有样本的平均轮廓系数
  4. 轮廓系数的范围为：[-1, 1]，值越大聚类效果越好

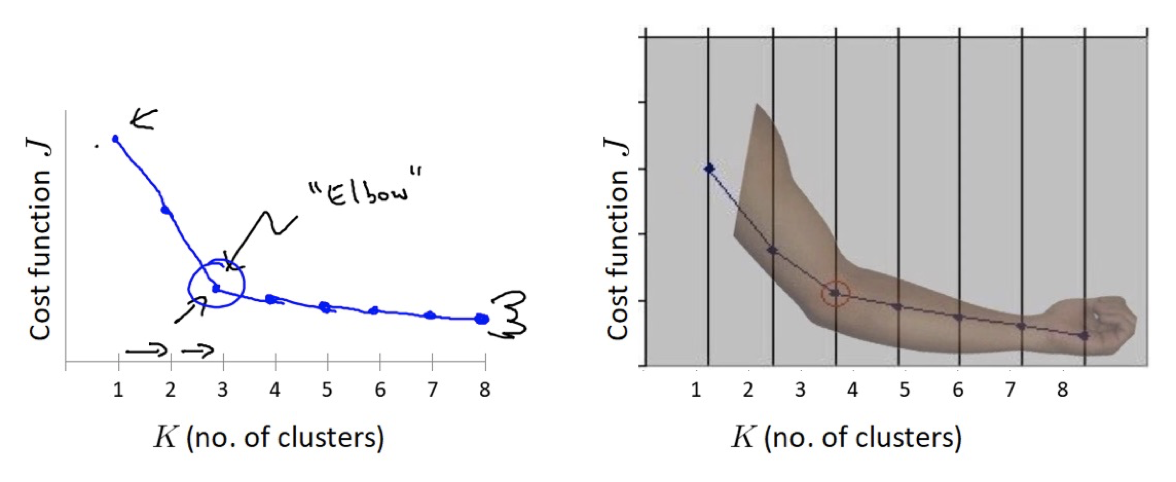
肘部法

肘部法可以用来确定 K 值.

  • 对于n个点的数据集，迭代计算 k from 1 to n，每次聚类完成后计算 SSE

  • SSE 是会逐渐变小的，因为每个点都是它所在的簇中心本身。

  • SSE 变化过程中会出现一个拐点，下降率突然变缓时即认为是最佳 n_clusters 值。

  • 在决定什么时候停止训练时，肘形判据同样有效，数据通常有更多的噪音，在增加分类无法带来更多回报时，我们停止增加类别。

CH 系数

CH值越大越好

CH 系数结合了聚类的凝聚度（Cohesion）和分离度（Separation）、质心的个数，希望用最少的簇进行聚类。

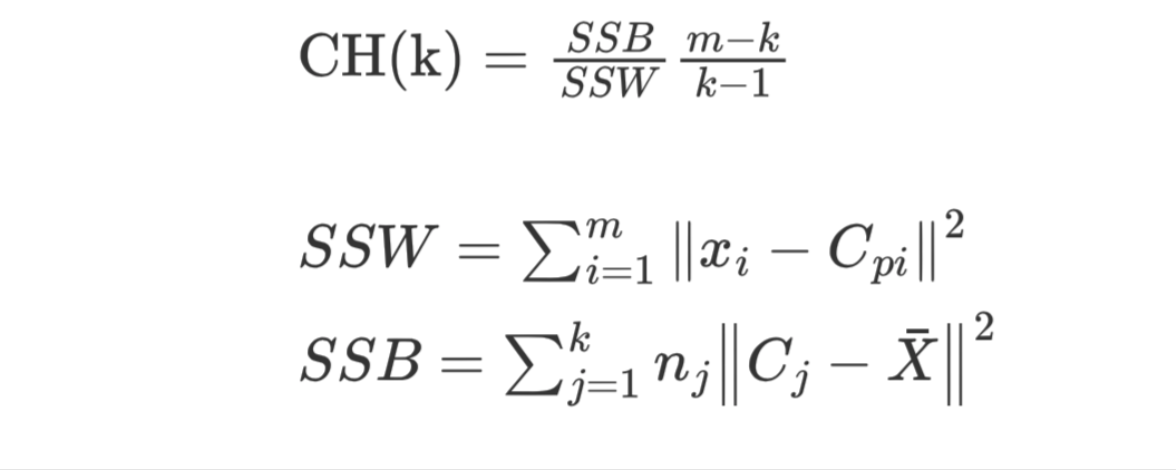
SSW 的含义：

  1. Cpi 表示质心
  2. xi 表示某个样本
  3. SSW 值是计算每个样本点到质心的距离，并累加起来
  4. SSW 表示表示簇内的内聚程度，越小越好
  5. m 表示样本数量
  6. k 表示质心个数

SSB 的含义：

  1. Cj 表示质心，X 表示质心与质心之间的中心点，nj 表示样本的个数
  2. SSB 表示簇与簇之间的分离度，SSB 越大越好

聚类评估的使用

python 复制代码 
# 这块代码了解即可，为了防止使用KMeans出现内存泄露OOM
import os
os.environ['OMP_NUM_THREADS'] = '4'

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn.metrics import silhouette_score # SC轮廓系数
from sklearn.metrics import calinski_harabasz_score # CH轮廓系数

# 通过SSE指标评价KMeans聚类效果
def sse():
    # 1- 生成数据
    """
        n_samples：按照高斯分布随机生成多少个样本
        n_features：特征字段个数
        centers：质心的坐标位置
        cluster_std：簇的标准差。标准差越大，那么样本越分散
        random_state：随机数种子
    """
    x,y = make_blobs(
        n_samples=1000,
        n_features=2,
        centers=[[-1,-1],[0,0],[1,1],[2,2]],
        cluster_std=[0.4,0.2,0.2,0.2],
        random_state=510
    )

    # 2- 因为是要研究n_clusters超参数与SSE评估指标间的关系，因此要使用循环
    sse_list = []
    for n_clusters in range(1,100):
        estimator = KMeans(n_clusters)
        y_predict = estimator.fit_predict(x)

        # 计算SSE的值
        sse_value = estimator.inertia_
        # 使用有序的list存储SSE的值。避免乱序
        sse_list.append(sse_value)

    # 3- 画图：绘制n_clusters超参数与SSE评估指标间的折线图
    # 3.1- 创建画布
    plt.figure(figsize=(20,10),dpi=200)
    # 3.2- 画折线图
    plt.plot(range(1,100), sse_list, c="r")
    # 3.3- 折线优化
    plt.xlabel("k")
    plt.ylabel("sse")
    # 刻度
    plt.xticks(range(0,101,2))
    # 网格线
    plt.grid()
    # 3.4- 展示
    plt.savefig("./data/sse.png") # 注意：图片保存需要在show()之前执行
    plt.show()

# 通过SC指标评价KMeans聚类效果
def sc():
    # 1- 生成数据
    """
        n_samples：按照高斯分布随机生成多少个样本
        n_features：特征字段个数
        centers：质心的坐标位置
        cluster_std：簇的标准差。标准差越大，那么样本越分散
        random_state：随机数种子
    """
    x,y = make_blobs(
        n_samples=1000,
        n_features=2,
        centers=[[-1,-1],[0,0],[1,1],[2,2]],
        cluster_std=[0.4,0.2,0.2,0.2],
        random_state=510
    )

    # 2- 因为是要研究n_clusters超参数与SC评估指标间的关系，因此要使用循环
    """
        因为SC轮廓系数要计算样本与其他簇之间的距离值，因此n_clusters参数值至少是2。否则会报如下的错误：
        ValueError: Number of labels is 1. Valid values are 2 to n_samples - 1 (inclusive)
        
        另外，plt画图的时候，横轴的其实点也要与这里for循环中的range保持一致
    """
    sc_list = []
    for n_clusters in range(2,100):
        estimator = KMeans(n_clusters)
        y_predict = estimator.fit_predict(x)

        # 计算SC的值
        sc_value = silhouette_score(x,y_predict)
        # 使用有序的list存储SC的值。避免乱序
        sc_list.append(sc_value)

    # 3- 画图：绘制n_clusters超参数与SC评估指标间的折线图
    # 3.1- 创建画布
    plt.figure(figsize=(20,10),dpi=200)
    # 3.2- 画折线图
    plt.plot(range(2,100), sc_list, c="r")
    # 3.3- 折线优化
    plt.xlabel("k")
    plt.ylabel("sse")
    # 刻度
    plt.xticks(range(0,101,2))
    # 网格线
    plt.grid()
    # 3.4- 展示
    plt.savefig("./data/sc.png") # 注意：图片保存需要在show()之前执行
    plt.show()


# 通过CH指标评价KMeans聚类效果
def ch():
    # 1- 生成数据
    """
        n_samples：按照高斯分布随机生成多少个样本
        n_features：特征字段个数
        centers：质心的坐标位置
        cluster_std：簇的标准差。标准差越大，那么样本越分散
        random_state：随机数种子
    """
    x, y = make_blobs(
        n_samples=1000,
        n_features=2,
        centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
        cluster_std=[0.4, 0.2, 0.2, 0.2],
        random_state=510
    )

    # 2- 因为是要研究n_clusters超参数与CH评估指标间的关系，因此要使用循环
    """
        因为CH轮廓系数要计算样本与其他簇之间的距离值，因此n_clusters参数值至少是2。否则会报如下的错误：
        ValueError: Number of labels is 1. Valid values are 2 to n_samples - 1 (inclusive)

        另外，plt画图的时候，横轴的其实点也要与这里for循环中的range保持一致
    """
    ch_list = []
    for n_clusters in range(2, 100):
        estimator = KMeans(n_clusters)
        y_predict = estimator.fit_predict(x)

        # 计算CH的值
        ch_value = calinski_harabasz_score(x, y_predict)
        # 使用有序的list存储CH的值。避免乱序
        ch_list.append(ch_value)

    # 3- 画图：绘制n_clusters超参数与CH评估指标间的折线图
    # 3.1- 创建画布
    plt.figure(figsize=(20, 10), dpi=200)
    # 3.2- 画折线图
    plt.plot(range(2, 100), ch_list, c="r")
    # 3.3- 折线优化
    plt.xlabel("k")
    plt.ylabel("sse")
    # 刻度
    plt.xticks(range(0, 101, 2))
    # 网格线
    plt.grid()
    # 3.4- 展示
    plt.savefig("./data/ch.png")  # 注意：图片保存需要在show()之前执行
    plt.show()

if __name__ == '__main__':
    """
        总结：
            1- SSE越小越好，最优超参数通过肘方法找到
            2- SC越大越好，范围在[-1,1]
            3- CH越大越好
    """
    # sse()
    # sc()
    ch()

五、案例

案例介绍

已知：客户性别、年龄、年收入、消费指数

需求：对客户进行分析，找到业务突破口，寻找黄金客户

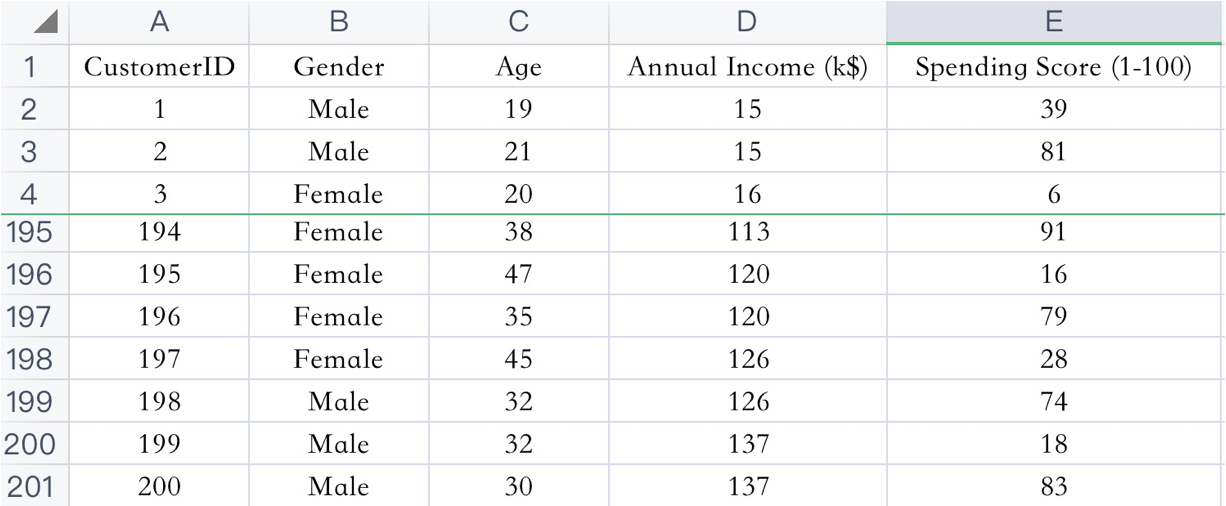
数据集共包含顾客的数据, 数据共有 4 个特征, 数据共有 200 条。接下来，使用聚类算法对具有相似特征的的顾客进行聚类，并可视化聚类结果。

案例实现

python 复制代码 
# 这块代码了解即可，为了防止使用KMeans出现内存泄露OOM
import os
os.environ['OMP_NUM_THREADS'] = '1'

import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn.metrics import silhouette_score # SC轮廓系数

# 获得最优的超参数n_clusters值
def get_n_clusters():
    # 1- 准备数据
    df = pd.read_csv("./data/customers.csv",encoding="UTF-8")

    # 2- 选择特征。只分析Annual Income (k$),Spending Score (1-100)这两个特征列
    x = df.iloc[:,3:]
    # print(x)

    # 3- 获得最优的超参数
    sse_list = []
    sc_list = []

    for n_clusters in range(2,50):
        estimator = KMeans(n_clusters)
        y_predict = estimator.fit_predict(x)

        # 计算SSE值
        sse_value = estimator.inertia_
        sse_list.append(sse_value)

        # 计算SC值
        sc_value = silhouette_score(x, y_predict)
        sc_list.append(sc_value)

    # 4- 绘制n_clusters与SSE值的关系
    plt.figure(figsize=(20, 10), dpi=200)
    plt.plot(range(2,50), sse_list, c="r")
    plt.xticks(range(0, 50))
    plt.title("sse")
    plt.grid()
    plt.show()

    # 5- 绘制n_clusters与SC值的关系
    plt.figure(figsize=(20, 10), dpi=200)
    plt.plot(range(2, 50), sc_list, c="r")
    plt.xticks(range(0, 50))
    plt.title("sc")
    plt.grid()
    plt.show()

# 进行聚类分析
def kmeans_ml():
    # 1- 准备数据
    df = pd.read_csv("./data/customers.csv", encoding="UTF-8")

    # 2- 选择特征。只分析Annual Income (k$),Spending Score (1-100)这两个特征列
    x = df.iloc[:, 3:]

    # 3- 机器学习
    estimator = KMeans(n_clusters=5)

    # 4- 训练和预测
    y_predict = estimator.fit_predict(x)

    # 5- 绘制散点图：5个簇的散点、5个质心
    plt.scatter(x.values[y_predict==0,0], x.values[y_predict==0,1],s=100, c="red")
    plt.scatter(x.values[y_predict==1,0], x.values[y_predict==1,1],s=100, c="blue")
    plt.scatter(x.values[y_predict==2,0], x.values[y_predict==2,1],s=100, c="green")
    plt.scatter(x.values[y_predict==3,0], x.values[y_predict==3,1],s=100, c="pink")
    plt.scatter(x.values[y_predict==4,0], x.values[y_predict==4,1],s=100, c="purple")

    # 绘制5个质心
    plt.scatter(estimator.cluster_centers_[:,0], estimator.cluster_centers_[:,1], c="black", s=300)
    # print("5个质心的信息：",estimator.cluster_centers_)

    plt.xlabel("Annual Income (k$)")
    plt.ylabel("Spending Score (1-100)")
    plt.legend()
    plt.show()

# 解释x.values[y_predict==0,0]
import numpy as np
def 解释():
    # 演示数据[[15,39],[15,81],[16,6],[16,77]]
    my_list = [[15,39],[15,81],[16,6],[16,77]]
    my_array = np.array(my_list)
    # print(my_array, type(my_array))

    result_1 = my_array[[True, False,  False, True]]
    #                 [[15,39],[15,81],[16,6],[16,77]]
    # print(result_1)

    result_2 = my_array[[True, False, False, True], 0]
    print(result_2)

    result_3 = my_array[[True, False, False, True], 1]
    print(result_3)

if __name__ == '__main__':
    # 获得最优超参数。结果是5
    # get_n_clusters()
    kmeans_ml()

    # 解释()
相关推荐
C嘎嘎嵌入式开发5 小时前
(二) 机器学习之卷积神经网络
人工智能·机器学习·cnn
递归不收敛6 小时前
吴恩达机器学习课程（PyTorch 适配）学习笔记：3.4 强化学习
pytorch·学习·机器学习
StarPrayers.6 小时前
卷积层（Convolutional Layer）学习笔记
人工智能·笔记·深度学习·学习·机器学习
lisw056 小时前
AIoT（人工智能物联网）：融合范式下的技术演进、系统架构与产业变革
大数据·人工智能·物联网·机器学习·软件工程
递归不收敛7 小时前
吴恩达机器学习课程（PyTorch适配）学习笔记：1.4 模型评估与问题解决
pytorch·学习·机器学习
小喵要摸鱼8 小时前
【机器学习】无监督学习 —— K-Means 聚类、DBSCAN 聚类
机器学习·kmeans·聚类·dbscan
Christo38 小时前
关于K-means和FCM的凸性问题讨论
人工智能·算法·机器学习·数据挖掘·kmeans
春末的南方城市9 小时前
清华&字节开源HuMo: 打造多模态可控的人物视频，输入文字、图片、音频，生成电影级的视频，Demo、代码、模型、数据全开源。
人工智能·深度学习·机器学习·计算机视觉·aigc
深栈11 小时前
机器学习：决策树
人工智能·python·决策树·机器学习·sklearn
热门推荐
01两千字总结：Codex 国内如何安装和使用的教程，以及如何设置中文回答02GitHub 镜像站点03UV安装并设置国内源04KGG转MP3工具|非KGM文件|解密音频05Linux下V2Ray安装配置指南06jdk21下载、安装（Windows、Linux、macOS）07DeepSeek-VL 解析：混合视觉-语言模型如何超越传统计算机视觉方法08一文了解国产算子编程语言 TileLang，TileLang 对国产开源生态的影响与启示09Claude Code & 智谱GLM-4.5 环境配置指南 (Windows/macOS/Ubuntu)1046个Nano-banana 精选提示词，持续更新中