文章目录
- [1. 预备知识](#1. 预备知识)
-
- [1.1 特征值和特征向量](#1.1 特征值和特征向量)
- [1.2 特征值和特征向量的几何意义](#1.2 特征值和特征向量的几何意义)
- [1.3 特征值和特征向量的计算](#1.3 特征值和特征向量的计算)
- [1.4 矩阵对角化（Diagonal Decomposition）](#1.4 矩阵对角化（Diagonal Decomposition）)
- [1.5 归一化特征向量](#1.5 归一化特征向量)
- [1.6 奇异值分解（Singular Value Decomposition，SVD）](#1.6 奇异值分解（Singular Value Decomposition，SVD）)
- [2. PCA](#2. PCA)
- [2.1 降维（Dimensionality Reduction）](#2.1 降维（Dimensionality Reduction）)
- [2.2 主成分分析（Principal Component Analysis，PCA）](#2.2 主成分分析（Principal Component Analysis，PCA）)
-
- [2.2.1 PCA的优势](#2.2.1 PCA的优势)
- [2.2.2 PCA的局限性](#2.2.2 PCA的局限性)
- [2.2.3 应用](#2.2.3 应用)
- [3. 无监督学习](#3. 无监督学习)
-
- [3.1 赫布学习（Hebbian Learning）](#3.1 赫布学习（Hebbian Learning）)
- [3.2 奥贾规则（Oja's Rule）](#3.2 奥贾规则（Oja's Rule）)
-
- [3.2.1 放缩（Deflation）](#3.2.1 放缩（Deflation）)
- [3.3 主成分分析（PCA）在神经网络中的应用](#3.3 主成分分析（PCA）在神经网络中的应用)
- [3.4 自编码器（autoencoder）](#3.4 自编码器（autoencoder）)
-
- [3.4.1 深度自编码器（Deep Auto-encoder）](#3.4.1 深度自编码器（Deep Auto-encoder）)
- [3.4.2 去噪自编码器（Denoising Auto-encoder）](#3.4.2 去噪自编码器（Denoising Auto-encoder）)
- [3.4.3 自编码器网络（Auto-encoders Network）](#3.4.3 自编码器网络（Auto-encoders Network）)
- [3.5 聚类分析（Clustering Analysis）](#3.5 聚类分析（Clustering Analysis）)
-
- [3.5.1 K-means算法](#3.5.1 K-means算法)
- [3.6 无监督竞争学习（Unsupervised Competitive Learning）](#3.6 无监督竞争学习（Unsupervised Competitive Learning）)
-
- [3.6.1 无监督竞争学习的结构](#3.6.1 无监督竞争学习的结构)
- [3.6.2 赢者通吃（Winner-takes-all， WTA）](#3.6.2 赢者通吃（Winner-takes-all， WTA）)
- [3.6.3 简单竞争学习（Simple Competitive Learning）](#3.6.3 简单竞争学习（Simple Competitive Learning）)
-
- [3.6.3.1 公平竞争（Enforcing Fairer Competition）](#3.6.3.1 公平竞争（Enforcing Fairer Competition）)
- [3.6.3.2 漏斗学习（Leaky Learning）](#3.6.3.2 漏斗学习（Leaky Learning）)
1. 预备知识
1.1 特征值和特征向量
对于一个方阵 A A A，如果存在一个非零向量 m a t h b f v mathbf{v} mathbfv和一个标量 λ λ λ，使得：
A v = λ v A\mathbf{v} = \lambda \mathbf{v} Av=λv
那么：
v \mathbf{v} v称为矩阵 A A A的特征向量（eigenvector），
λ λ λ称为对应的特征值（eigenvalue）。
下图展示了一个例子。
这里， [ 1 1 ] \begin{bmatrix} 1 \\ 1 \end{bmatrix} [11]是特征向量，
3 3 3是特征值。
同理下面的例子中。
特征值 λ = 2 λ=2 λ=2，特征向量 v = [ 1 2 ] \mathbf{v}=\begin{bmatrix} 1 \\ 2 \end{bmatrix} v=[12]。
对于一个 m × m m×m m×m的方阵 S S S，最多有 m m m个不同的特征值。这是因为特征值是特征方程 d e t ( S − λ I ) = 0 det(S−λI)=0 det(S−λI)=0的解，而这个方程是一个 m m m次多项式方程，最多有 m m m个不同的根。
S v = λ v S\mathbf{v}=λ\mathbf{v} Sv=λv可以重写为 ( S − λ I ) v = 0 (S−λI)\mathbf{v}=0 (S−λI)v=0。这个方程只有非零解（即特征向量）当且仅当 d e t ( S − λ I ) = 0 det(S−λI)=0 det(S−λI)=0。
对于对称矩阵，如果对应的特征值不同，那么对应的特征向量是正交的。这意味着如果 λ 1 ≠ λ 2 \quad \lambda_1 \neq \lambda_2 λ1=λ2 ，那么特征向量 v 1 \mathbf{v}_1 v1和 v 2 \mathbf{v}2 v2满足 v 1 ⋅ v 2 = 0 \mathbf{v}1 \cdot \mathbf{v}2 = 0 v1⋅v2=0
S v { 1 , 2 } = λ { 1 , 2 } v { 1 , 2 } , 且 λ 1 ≠ λ 2 ⇒ v 1 ⋅ v 2 = 0 S\mathbf{v}{\{1,2\}} = \lambda{\{1,2\}}\mathbf{v}{\{1,2\}}, \quad \text{且} \quad \lambda_1 \neq \lambda_2 \Rightarrow \mathbf{v}_1 \cdot \mathbf{v}_2 = 0 Sv{1,2}=λ{1,2}v{1,2},且λ1=λ2⇒v1⋅v2=0
所有实对称矩阵的特征值都是实数。
对于正半定矩阵，所有特征值都是非负的。这意味着如果 ∀ w ∈ R n , w T S w ≥ 0 , 则如果 S v = λ v ⇒ λ ≥ 0 \forall \mathbf{w} \in \mathbb{R}^n, \mathbf{w}^T S \mathbf{w} \geq 0, \quad \text{则如果} \quad S\mathbf{v} = \lambda \mathbf{v} \Rightarrow \lambda \geq 0 ∀w∈Rn,wTSw≥0,则如果Sv=λv⇒λ≥0
1.2 特征值和特征向量的几何意义
下图给出了一个例子去展示其的结合意义。
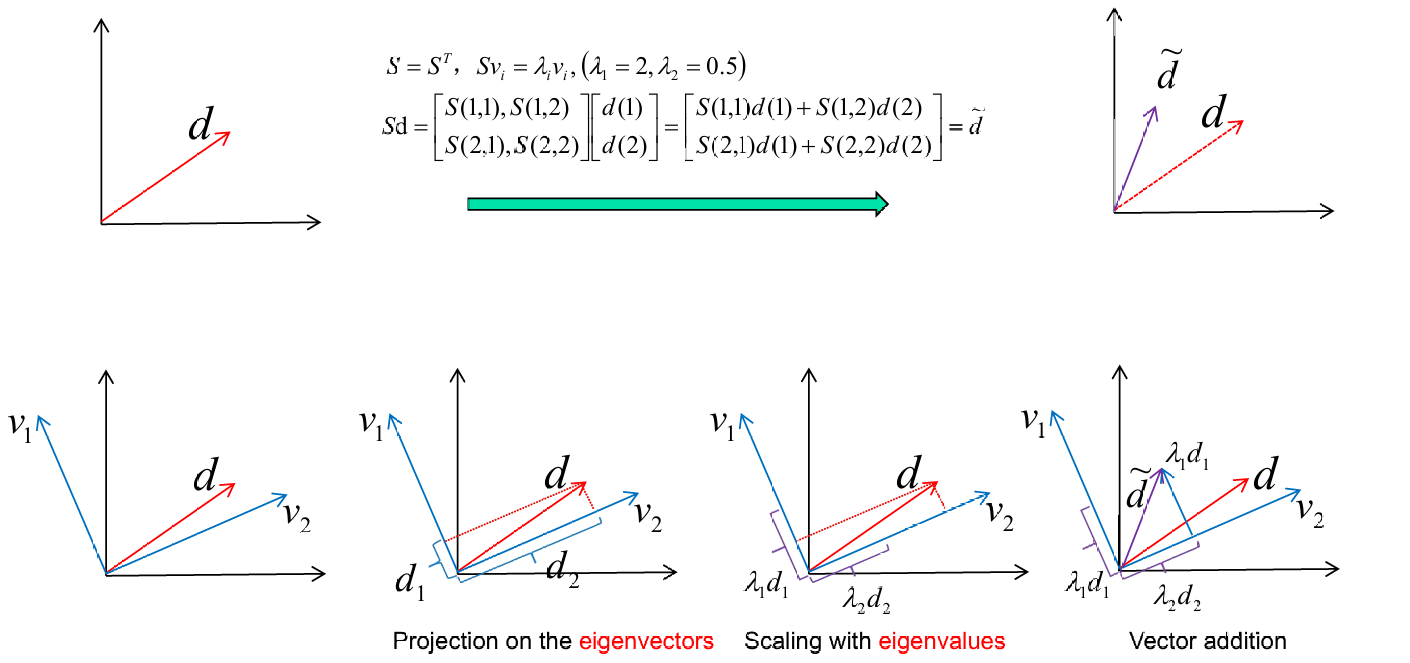
给定对称矩阵 S S S，满足 S = S T S = S^T S=ST，对于特征值 λ 1 = 2 \lambda_1 = 2 λ1=2和 λ 2 = 0.5 \lambda_2 = 0.5 λ2=0.5，有： S v i = λ i v i S\mathbf{v}_i = \lambda_i \mathbf{v}_i Svi=λivi其中 i = 1 , 2 i = 1, 2 i=1,2。
对于任意向量 d \mathbf{d} d，有： S d = [ S ( 1 , 1 ) S ( 1 , 2 ) S ( 2 , 1 ) S ( 2 , 2 ) ] [ d ( 1 ) d ( 2 ) ] = [ S ( 1 , 1 ) d ( 1 ) + S ( 1 , 2 ) d ( 2 ) S ( 2 , 1 ) d ( 1 ) + S ( 2 , 2 ) d ( 2 ) ] = d ~ S\mathbf{d} = \begin{bmatrix} S(1,1) & S(1,2) \\ S(2,1) & S(2,2) \end{bmatrix} \begin{bmatrix} d(1) \\ d(2) \end{bmatrix} =\begin{bmatrix} S(1,1)d(1) + S(1,2)d(2) \\ S(2,1)d(1) + S(2,2)d(2) \end{bmatrix} = \tilde{\mathbf{d}} Sd=[S(1,1)S(2,1)S(1,2)S(2,2)][d(1)d(2)]=[S(1,1)d(1)+S(1,2)d(2)S(2,1)d(1)+S(2,2)d(2)]=d~
我们将向量 d \mathbf{d} d投影到特征向量 v 1 \mathbf{v}_1 v1和 v 2 \mathbf{v}_2 v2上，得到 d 1 \mathbf{d}_1 d1和 d 2 \mathbf{d}_2 d2。如下图2所示。
将投影后的向量按对应的特征值 λ 1 \lambda_1 λ1和 λ 2 \lambda_2 λ2缩放，得到 λ 1 d 1 \lambda_1 \mathbf{d}_1 λ1d1和 λ 2 d 2 \lambda_2 \mathbf{d}_2 λ2d2。如下图3所示。
将缩放后的向量相加，得到最终的变换结果 d ~ \tilde{\mathbf{d}} d~。如下图4所示。
1.3 特征值和特征向量的计算
设矩阵 S S S为：
S = [ 2 1 1 2 ] S = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} S=[2112]
这是一个实对称矩阵。
计算特征值需要解特征方程 det ( S − λ I ) = 0 \det(S - \lambda I) = 0 det(S−λI)=0，其中 I I I是单位矩阵， λ \lambda λ是特征值。
S − λ I = [ 2 − λ 1 1 2 − λ ] S - \lambda I = \begin{bmatrix} 2-\lambda & 1 \\ 1 & 2-\lambda \end{bmatrix} S−λI=[2−λ112−λ]
计算行列式：
det ( S − λ I ) = ( 2 − λ ) 2 − 1 = 0 \det(S - \lambda I) = (2-\lambda)^2 - 1 = 0 det(S−λI)=(2−λ)2−1=0
解方程得到特征值：
( 2 − λ ) 2 − 1 = 0 ⇒ λ = 1 和 λ = 3 (2-\lambda)^2 - 1 = 0 \Rightarrow \lambda = 1 \text{ 和 } \lambda = 3 (2−λ)2−1=0⇒λ=1 和 λ=3
对于每个特征值，解方程 ( S − λ I ) v = 0 (S - \lambda I)\mathbf{v} = 0 (S−λI)v=0来找到对应的特征向量。
对于 λ 1 = 1 \lambda_1 = 1 λ1=1：
( S − I ) v = [ 1 1 1 1 ] [ x y ] = [ 0 0 ] (S - I)\mathbf{v} = \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} (S−I)v=[1111][xy]=[00]
得到特征向量：
v 1 = [ 1 − 1 ] \mathbf{v}_1 = \begin{bmatrix} 1 \\ -1 \end{bmatrix} v1=[1−1]
对于 λ 2 = 3 \lambda_2 = 3 λ2=3：
( S − 3 I ) v = [ − 1 1 1 − 1 ] [ x y ] = [ 0 0 ] (S - 3I)\mathbf{v} = \begin{bmatrix} -1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} (S−3I)v=[−111−1][xy]=[00]
得到特征向量：
v 2 = [ 1 1 ] \mathbf{v}_2 = \begin{bmatrix} 1 \\ 1 \end{bmatrix} v2=[11]
特征向量 v 1 \mathbf{v}_1 v1和 v 2 \mathbf{v}_2 v2是正交的，因为它们的点积为零：
v 1 ⋅ v 2 = 1 ⋅ 1 + ( − 1 ) ⋅ 1 = 0 \mathbf{v}_1 \cdot \mathbf{v}_2 = 1 \cdot 1 + (-1) \cdot 1 = 0 v1⋅v2=1⋅1+(−1)⋅1=0
1.4 矩阵对角化（Diagonal Decomposition）
设 S S S是一个 m × m m×m m×m的方阵，如果 S S S有 m m m个线性无关的特征向量，那么 S S S可以进行对角化。
定理指出存在一个特征分解，使得 S S S可以表示为 S = U Λ U − 1 S = U \Lambda U^{-1} S=UΛU−1其中 Λ \Lambda Λ是对角矩阵。
U U U的列是 S S S的特征向量， Λ \Lambda Λ的对角元素是 S S S的特征值，且按非递减顺序排列，即 Λ = diag ( λ 1 , ... , λ m ) , λ i ≥ λ i + 1 \Lambda = \text{diag}(\lambda_1, \ldots, \lambda_m), \quad \lambda_i \geq \lambda_{i+1} Λ=diag(λ1,...,λm),λi≥λi+1
设 U U U为特征向量构成的矩阵：
U = [ v 1 v 2 ⋯ v m ] U = \begin{bmatrix} \mathbf{v}_1 & \mathbf{v}_2 & \cdots & \mathbf{v}_m \end{bmatrix} U=[v1v2⋯vm]
S U SU SU的计算可以表示为：
S U = S [ v 1 v 2 ⋯ v m ] = [ S v 1 S v 2 ⋯ S v m ] = [ λ 1 v 1 λ 2 v 2 ⋯ λ m v m ] SU = S \begin{bmatrix} \mathbf{v}_1 & \mathbf{v}_2 & \cdots & \mathbf{v}_m \end{bmatrix} = \begin{bmatrix} S\mathbf{v}_1 & S\mathbf{v}_2 & \cdots & S\mathbf{v}_m \end{bmatrix} = \begin{bmatrix} \lambda_1\mathbf{v}_1 & \lambda_2\mathbf{v}_2 & \cdots & \lambda_m\mathbf{v}_m \end{bmatrix} SU=S[v1v2⋯vm]=[Sv1Sv2⋯Svm]=[λ1v1λ2v2⋯λmvm]
对角矩阵 Λ \Lambda Λ表示为：
Λ = [ λ 1 0 ⋯ 0 0 λ 2 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ λ m ] \Lambda = \begin{bmatrix} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_m \end{bmatrix} Λ= λ10⋮00λ2⋮0⋯⋯⋱⋯00⋮λm
由于 S U = U Λ SU=UΛ SU=UΛ，两边同时左乘 U − 1 U_{−1} U−1得到： U − 1 S U = Λ U^{-1}SU = \Lambda U−1SU=Λ
因此，原始矩阵 S S S可以表示为： S = U Λ U − 1 S = U\Lambda U^{-1} S=UΛU−1
我们现在回到前面的例子。
给定矩阵 S S S：
S = [ 2 1 1 2 ] S = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} S=[2112]
特征值 λ 1 = 1 \lambda_1 = 1 λ1=1和 λ 2 = 3 \lambda_2 = 3 λ2=3。
特征向量为：
( 1 − 1 ) 和 ( 1 1 ) \begin{pmatrix} 1 \\ -1 \end{pmatrix} \quad \text{和} \quad \begin{pmatrix} 1 \\ 1 \end{pmatrix} (1−1)和(11)
形成矩阵 U U U：
U = [ 1 1 − 1 1 ] U = \begin{bmatrix} 1 & 1 \\ -1 & 1 \end{bmatrix} U=[1−111]
计算 U U U的逆矩阵：
U − 1 = [ 1 2 − 1 2 1 2 1 2 ] U^{-1} = \begin{bmatrix} \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{bmatrix} U−1=[2121−2121]
验证 U U − 1 = I UU^{-1} = I UU−1=I：
U U − 1 = [ 1 0 0 1 ] = I UU^{-1} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = I UU−1=[1001]=I
对角矩阵 Λ \Lambda Λ包含特征值：
Λ = [ 1 0 0 3 ] \Lambda = \begin{bmatrix} 1 & 0 \\ 0 & 3 \end{bmatrix} Λ=[1003]
计算 S S S：
S = U Λ U − 1 = [ 1 1 − 1 1 ] [ 1 0 0 3 ] [ 1 2 − 1 2 1 2 1 2 ] S = U \Lambda U^{-1} = \begin{bmatrix} 1 & 1 \\ -1 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 3 \end{bmatrix} \begin{bmatrix} \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{bmatrix} S=UΛU−1=[1−111][1003][2121−2121]
这个计算结果等于原始矩阵 S S S，符合我们前面的结论。
1.5 归一化特征向量
我们当然可以再应用归一化。这样我们得到的矩阵就是正交的。
定理：如果 S S S 是一个 m × m m \times m m×m的实对称矩阵，那么存在一个特征分解，其中矩阵 Q Q Q是正交的。这意味着：
S = Q Λ Q T S = Q \Lambda Q^T S=QΛQT
其中：
Q Q Q是一个正交矩阵，其列是 S S S的归一化特征向量。
Λ \Lambda Λ是一个对角矩阵，其对角线上的元素是 S S S的特征值。
正交矩阵 Q Q Q的性质：
Q − 1 = Q T Q^{-1} = Q^T Q−1=QT：正交矩阵的逆等于其转置。
Q Q Q的列是归一化的特征向量：这意味着每个特征向量的长度为1。
Q Q Q的列是正交的：这意味着任意两个不同的特征向量的点积为0。
这种分解表明，存在一个坐标变换（由 Q Q Q给出），在这个新坐标系中，矩阵 S S S的作用仅仅是通过特征值进行缩放，而不改变方向。由于 Q Q Q是正交的，这种变换保持了向量的长度和角度，即保持了几何形状。
1.6 奇异值分解（Singular Value Decomposition，SVD）
对于一个 m × n m \times n m×n的矩阵 A A A（秩为 r r r），存在一个分解：
A = U Σ V T A = U \Sigma V^T A=UΣVT
其中：
U U U是一个 m × m m \times m m×m的正交矩阵，其列是 A A T AA^T AAT的正交特征向量。
Σ \Sigma Σ是一个 m × n m \times n m×n的对角矩阵，对角线上的元素是非负实数，称为奇异值。
V V V是一个 n × n n \times n n×n的正交矩阵，其列是 A T A A^TA ATA的正交特征向量。
奇异值 σ i \sigma_i σi与 A T A A^TA ATA的特征值 λ i \lambda_i λi的关系为：
σ i = λ i \sigma_i = \sqrt{\lambda_i} σi=λi
其中 λ i \lambda_i λi是 A T A A^TA ATA的特征值。
Σ Σ Σ矩阵的对角线元素就是这些奇异值。
Σ = diag ( σ 1 , σ 2 , ... , σ r ) \Sigma = \text{diag}(\sigma_1, \sigma_2, \ldots, \sigma_r) Σ=diag(σ1,σ2,...,σr)
下面给出一个例子。
A = [ 1 − 1 0 1 1 0 ] A = \begin{bmatrix} 1 & -1 \\ 0 & 1 \\ 1 & 0 \end{bmatrix} A= 101−110
矩阵 A A A的 SVD 分解为：
A = U Σ V T A = U \Sigma V^T A=UΣVT
其中：
U U U是一个 3 × 3 3 \times 3 3×3的正交矩阵：
U = [ 0 2 6 1 3 1 2 − 1 6 1 3 1 2 1 6 − 1 3 ] U = \begin{bmatrix} 0 & \frac{2}{\sqrt{6}} & \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{6}} & \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{3}} \end{bmatrix} U= 02 12 16 2−6 16 13 13 1−3 1
Σ \Sigma Σ是一个 3 × 2 3 \times 2 3×2 的对角矩阵，包含非负实数（奇异值）：
Σ = [ 1 0 0 3 0 0 ] \Sigma = \begin{bmatrix} 1 & 0 \\ 0 & \sqrt{3} \\ 0 & 0 \end{bmatrix} Σ= 10003 0
V T V^T VT是一个 2 × 2 2 \times 2 2×2的正交矩阵的转置：
V T = [ 1 2 1 2 1 2 − 1 2 ] V^T = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{bmatrix} VT=[2 12 12 1−2 1]
2. PCA
2.1 降维（Dimensionality Reduction）
处理高维数据的一种方法是通过降低它们的维度来简化数据。这有助于减少计算复杂性，去除冗余信息，并可能提高模型的性能。
可以使用线性变换进行降维，将高维数据投影到一个更低维的子空间中，可以使用线性或非线性变换来实现。
如果 X X X是一个 d × N d×N d×N的数据矩阵（其中 d d d是原始数据的维度， N N N是样本数量），我们可以通过一个 k × d k×d k×d的矩阵 U（其中 k ≪ d k≪d k≪d）将其转换为一个 k × N k×N k×N的矩阵 Y Y Y： Y = U X Y=UX Y=UX
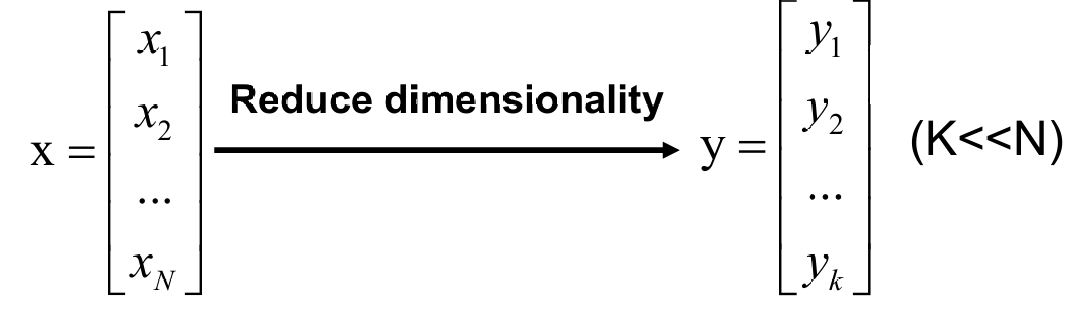
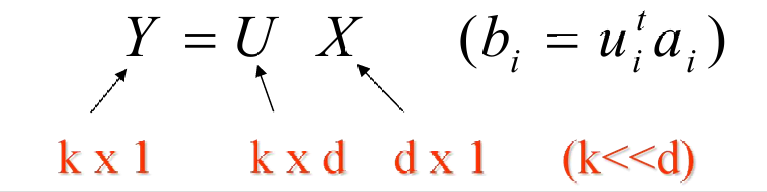
这里， Y Y Y是降维后的数据， k k k是目标维度，远小于原始维度 d d d。
基向量：在原始的 N N N维空间中，任何向量 x \mathbf{x} x都可以表示为一组基向量 v 1 , v 2 , ... , v N \mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_N v1,v2,...,vN的线性组合：
x = a 1 v 1 + a 2 v 2 + ... + a N v N \mathbf{x} = a_1 \mathbf{v}_1 + a_2 \mathbf{v}_2 + \ldots + a_N \mathbf{v}_N x=a1v1+a2v2+...+aNvN
其中 a 1 , a 2 , ... , a N a_1, a_2, \ldots, a_N a1,a2,...,aN是系数。
低维子空间表示：在低维子空间中，我们寻找一组新的基向量 u 1 , u 2 , ... , u K \mathbf{u}_1, \mathbf{u}_2, \ldots, \mathbf{u}_K u1,u2,...,uK（其中 K < N K < N K<N），使得原始向量 x \mathbf{x} x可以近似表示为这些新基向量的线性组合：
x ^ = b 1 u 1 + b 2 u 2 + ... + b K u K \hat{\mathbf{x}} = b_1 \mathbf{u}_1 + b_2 \mathbf{u}_2 + \ldots + b_K \mathbf{u}_K x^=b1u1+b2u2+...+bKuK
其中 b 1 , b 2 , ... , b K b_1, b_2, \ldots, b_K b1,b2,...,bK是新的系数。
下面我们看一个例子。
原始空间表示：
标准基向量 v 1 , v 2 , v 3 \mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3 v1,v2,v3：
v 1 = [ 1 0 0 ] , v 2 = [ 0 1 0 ] , v 3 = [ 0 0 1 ] \mathbf{v}_1 = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}, \quad \mathbf{v}_2 = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}, \quad \mathbf{v}_3 = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} v1= 100 ,v2= 010 ,v3= 001
这些是三维空间的标准基向量。
向量 x v \mathbf{x}_v xv：
x v = [ 3 3 3 ] = 3 v 1 + 3 v 2 + 3 v 3 \mathbf{x}_v = \begin{bmatrix} 3 \\ 3 \\ 3 \end{bmatrix} = 3\mathbf{v}_1 + 3\mathbf{v}_2 + 3\mathbf{v}_3 xv= 333 =3v1+3v2+3v3
这里，向量 x v \mathbf{x}_v xv在标准基下表示为 3 v 1 + 3 v 2 + 3 v 3 3\mathbf{v}_1 + 3\mathbf{v}_2 + 3\mathbf{v}_3 3v1+3v2+3v3。
其他基表示：
其他基向量 u 1 , u 2 , u 3 \mathbf{u}_1, \mathbf{u}_2, \mathbf{u}_3 u1,u2,u3：
u 1 = [ 1 0 0 ] , u 2 = [ 1 1 0 ] , u 3 = [ 1 1 1 ] \mathbf{u}_1 = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}, \quad \mathbf{u}_2 = \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}, \quad \mathbf{u}_3 = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} u1= 100 ,u2= 110 ,u3= 111
这些是三维空间中的另一组基向量。
向量 x u \mathbf{x}_u xu：
x u = [ 3 3 3 ] = 0 u 1 + 0 u 2 + 3 u 3 \mathbf{x}_u = \begin{bmatrix} 3 \\ 3 \\ 3 \end{bmatrix} = 0\mathbf{u}_1 + 0\mathbf{u}_2 + 3\mathbf{u}_3 xu= 333 =0u1+0u2+3u3
这里，向量 x u \mathbf{x}_u xu在新的基 u 1 , u 2 , u 3 \mathbf{u}_1, \mathbf{u}_2, \mathbf{u}_3 u1,u2,u3下表示为 0 u 1 + 0 u 2 + 3 u 3 0\mathbf{u}_1 + 0\mathbf{u}_2 + 3\mathbf{u}_3 0u1+0u2+3u3。
x v = x u \mathbf{x}_v = \mathbf{x}_u xv=xu：尽管使用了不同的基向量来表示同一个向量，但最终表示的向量是相同的。
2.2 主成分分析（Principal Component Analysis，PCA）
PCA 是一种降维技术，它通过找到适当的变换来减少数据的维度。这种变换旨在满足某些特定的标准，例如最小化信息损失、最大化数据的区分度等。
PCA 的主要目标是在尽可能保留数据集中存在的变异性（即数据的分散程度或方差）的同时，降低数据的维度。这意味着 PCA 试图找到一个新坐标系，使得数据在这个新坐标系中的主要变异方向（即主成分）能够被保留下来，而次要的变异方向则被忽略或压缩。
PCA 通过计算数据协方差矩阵的特征向量和特征值来实现降维。特征向量表示数据的主要变异方向，而特征值表示这些方向上的变异程度。
根据特征值的大小，选择最大的几个特征值对应的特征向量作为主成分。这些主成分捕捉了数据集中最重要的变异信息。
将原始数据投影到由选定的主成分构成的新坐标系中，从而实现降维。
PCA 的一个主要目标是找到数据中具有高方差的方向。这些方向被认为是数据中最重要的特征，因为它们捕捉了数据的主要变异性。
PCA 试图用尽可能少的基向量来表示数据，同时保持较低的均方误差。
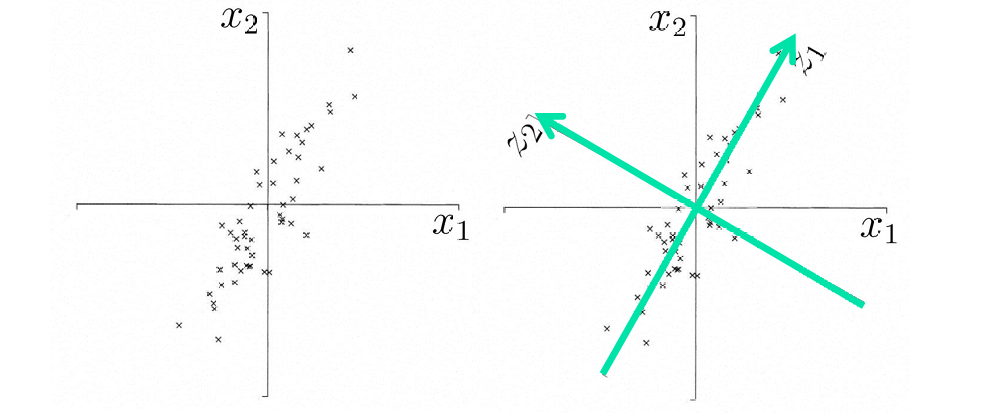
第一主成分是数据中方差最大的方向。这个方向捕捉了数据中最大的变异性。
后续的主成分是与第一主成分正交的方向，并且每个后续的主成分都是在剩余变异中捕捉最大方差的方向。
假设：
E [ x ] = 0 E[\mathbf{x}] = 0 E[x]=0表示数据的期望值为零。
a = x T q = q T x \mathbf{a} = \mathbf{x}^T \mathbf{q} = \mathbf{q}^T \mathbf{x} a=xTq=qTx表示 a \mathbf{a} a是 x \mathbf{x} x在 q \mathbf{q} q方向上的投影。
∥ q ∥ = ( q T q ) 1 / 2 = 1 \|\mathbf{q}\| = (\mathbf{q}^T \mathbf{q})^{1/2} = 1 ∥q∥=(qTq)1/2=1表示 q \mathbf{q} q是单位向量。
方差表示为： σ 2 = E [ a 2 ] − E [ a ] 2 = E [ a 2 ] \sigma^2 = E[a^2] - E[a]^2 = E[a^2] σ2=E[a2]−E[a]2=E[a2](由于 E [ x ] = 0 E[x]=0 E[x]=0，所以 E [ a ] = 0 E[a]=0 E[a]=0。)
进一步展开：
= E [ ( q T x ) ( x T q ) ] = q T E [ x x T ] q = q T R q = E[(\mathbf{q}^T \mathbf{x})(\mathbf{x}^T \mathbf{q})] = \mathbf{q}^T E[\mathbf{x}\mathbf{x}^T] \mathbf{q} = \mathbf{q}^T \mathbf{R} \mathbf{q} =E[(qTx)(xTq)]=qTE[xxT]q=qTRq
其中 R \mathbf{R} R是数据的协方差矩阵。
当 q \mathbf{q} q是协方差矩阵 R \mathbf{R} R的主成分时，方差被最大化。
主成分 q \mathbf{q} q可以通过协方差矩阵 R \mathbf{R} R的特征向量分解得到：
R = Q Λ Q T \mathbf{R} = \mathbf{Q} \boldsymbol{\Lambda} \mathbf{Q}^T R=QΛQT
其中 Q = [ q 1 , q 2 , ... , q m ] \mathbf{Q} = [\mathbf{q}_1, \mathbf{q}_2, \ldots, \mathbf{q}_m] Q=[q1,q2,...,qm]是特征向量矩阵， Λ = diag [ λ 1 , λ 2 , ... , λ m ] \boldsymbol{\Lambda} = \text{diag}[\lambda_1, \lambda_2, \ldots, \lambda_m] Λ=diag[λ1,λ2,...,λm]是对角矩阵，包含特征值。
对于每个 j j j：
R q j = λ j q j j = 1 , 2 , ... , m ⇔ R q = λ q \mathbf{R} \mathbf{q}_j = \lambda_j \mathbf{q}_j \quad j = 1, 2, \ldots, m\Leftrightarrow \mathbf{R} \mathbf{q} = \lambda \mathbf{q} Rqj=λjqjj=1,2,...,m⇔Rq=λq
下图展示了一个PCA的二维示例。
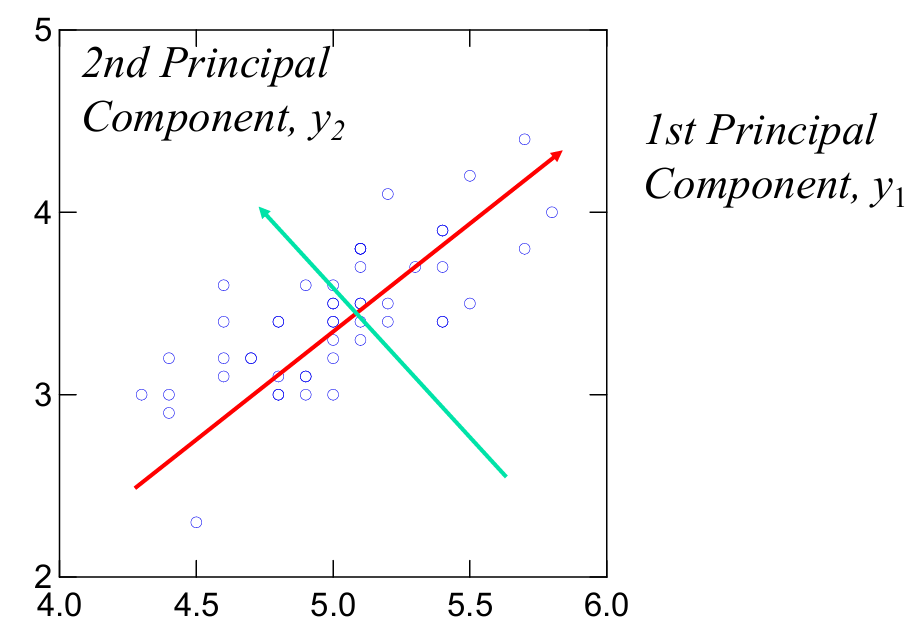
红色箭头表示第一主成分（ y 1 y_1 y1)，它是数据中方差最大的方向。换句话说，第一主成分捕捉了数据中最大的变异性。
绿色箭头表示第二主成分（ y 2 y_2 y2)，它是与第一主成分正交的方向，并且捕捉了在第一主成分之后剩余的最大变异性。
2.2.1 PCA的优势
PCA的优势如下：
- 降低原始数据的维度。
这样会减少训练过程中的时间消耗，提高效率。 - 丢弃原始数据中的一些被认为是不重要的信息。
如果被丢弃的信息主要是噪声（即无用或误导性的数据），那么 PCA 不仅可以提高数据处理的效率，还可以改善模型的性能，因为它减少了模型可能从噪声中学习到的不必要特征。
2.2.2 PCA的局限性
同样就刚刚最后一点我们也有其的弊端：
- 丢弃原始数据的一些信息。
如果这些丢失的信息对于分析或建模是重要的，那么应用 PCA 可能不是最佳选择。 - 主成分（Principal Component，简称 PC）或基向量可能难以解释。
在某些情况下，PCA 得到的主成分可能不容易直接与原始数据的特征联系起来，这使得结果的解释变得复杂。 - PCA 是一种线性模型，它假设数据的主要变异可以通过线性组合来解释。
这意味着 PCA 不适合处理非线性问题。 - PCA 通常假设第一主成分（即具有最大方差的方向）比其他主成分更重要。
然而，这种假设可能不总是成立，特别是在数据的变异性在多个方向上都很重要的情况下。
2.2.3 应用
我们可以使用PCA在人脸识别和图像处理上。
下面展示其应用。
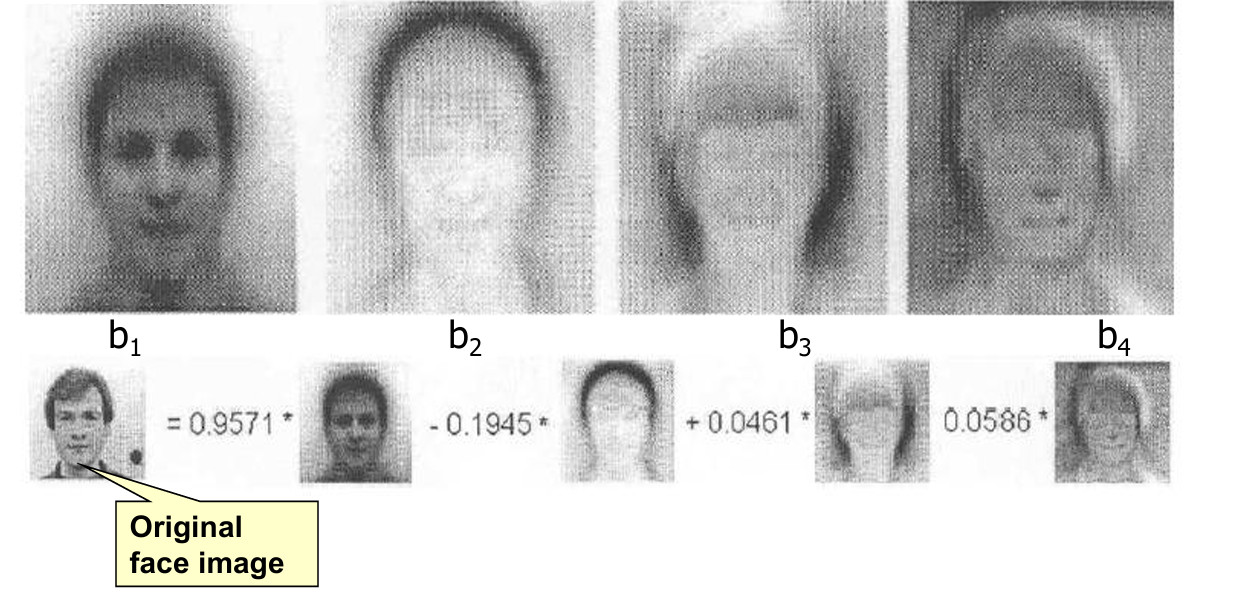每个特征脸都是数据集中变异性最大的方向，可以捕捉人脸图像数据的不同特征（如形状、表情等）。
通过这些特征脸，原始的人脸图像可以被近似表示为这些特征脸的线性组合。
3. 无监督学习
我们再一次谈到了无监督学习，这次是神经网络的无监督学习。
无监督学习是一种机器学习方法，其中模型从未标记的数据中学习。这意味着输入数据没有与之关联的期望输出或标签，模型需要自行发现数据中的结构和模式。
无监督学习网络的组成包含两部分：
- 前馈连接：无监督学习网络通常包含前馈连接，这是一种信息从输入层流向输出层的连接方式，类似于传统的神经网络结构。
- 局部学习元素：这些网络包含特定的元素或机制，以促进"局部"学习。这意味着网络能够识别和利用数据中的局部模式或结构，而不需要全局的标签信息。
3.1 赫布学习（Hebbian Learning）
赫布原则描述了神经元之间连接强度（即突触权重）的变化机制。具体来说，当一个神经元反复激活另一个神经元时，后者神经元的阈值会降低，或者两者之间的突触权重会增加。这实际上增加了第二个神经元被激活的可能性。
赫布学习规则的数学表达式为 Δ W j i = η y j x i \Delta W_{ji} = \eta y_j x_i ΔWji=ηyjxi，其中 η η η是学习率， y J y_J yJ是第 j j j个神经元的输出， x i x_i xi是第 i i i个神经元的输入。
赫布规则不需要期望或目标信号，因此它是一种无监督学习方法。这使得赫布学习适用于没有明确标签或目标值的情况，例如在特征学习或聚类任务中。
因此对于权重更新，考虑单个权重 w w w的更新（ x x x 和 y y y是突触前后的神经元活动）：
w ( n + 1 ) = w ( n ) + η x ( n ) y ( n ) w(n + 1) = w(n) + \eta x(n)y(n) w(n+1)=w(n)+ηx(n)y(n)
对于线性激活函数： w ( n + 1 ) = w ( n ) [ 1 + η x ( n ) x T ( n ) ] w(n + 1) = w(n)[1 + \eta x(n)x^T(n)] w(n+1)=w(n)[1+ηx(n)xT(n)]
权重增加无界限。如果初始权重为负，则它将在负方向增加。如果为正，则将在正方向增加。
赫布学习本质上是不稳定的，与使用 BP 算法（反向传播算法）的误差校正学习不同。
考虑一个具有 ρ ρ ρ个输入的单个线性神经元。
y = w T x = x T w y = \mathbf{w}^T \mathbf{x} = \mathbf{x}^T \mathbf{w} y=wTx=xTw
权重更新规则：
Δ w = η [ x 1 y x 2 y ... x p y ] T \Delta \mathbf{w} = \eta [\mathbf{x}_1 y \quad \mathbf{x}_2 y \quad \ldots \quad \mathbf{x}_p y]^T Δw=η[x1yx2y...xpy]T
其中， η η η是学习率， x i x_i xi是输入向量的第 i i i个分量， y y y是神经元的输出。
点积可以表示为：
y = ∣ w ∣ ∣ x ∣ cos ( α ) y = |\mathbf{w}||\mathbf{x}| \cos(\alpha) y=∣w∣∣x∣cos(α)
其中， α \alpha α是向量 x \mathbf{x} x和 w \mathbf{w} w之间的夹角。
如果 α \alpha α接近 0（ x \mathbf{x} x和 w \mathbf{w} w接近），则 y y y较大。
如果 α \alpha α接近 90（ x \mathbf{x} x和 w \mathbf{w} w远离），则 y y y接近零。
使用赫布学习训练的网络在其输入空间中创建了一个相似性度量，这个度量基于权重中包含的信息。换句话说，网络学习到了一种衡量输入数据相似性的方法。
在训练过程中，权重捕获（或记忆）了数据中的信息。这意味着网络通过调整权重来学习数据的特征和模式。
在网络操作期间，当权重固定时，如果输出 y y y很大，这表明当前输入与训练期间创建权重的输入 x x x相似。换句话说，网络能够识别出与训练数据相似的新输入。
3.2 奥贾规则（Oja's Rule）
简单的赫布学习规则会导致权重无限制地增加或减少。这意味着权重可能会变得非常大或非常小，从而影响学习过程的稳定性。
为了解决这个问题，需要对权重进行归一化处理，使其保持在一个合理的范围内。权重归一化可以通过除以权重的范数（即权重向量的模）来实现。
Oja's Rule的权重更新公式为：
w j i ( n + 1 ) = w j i ( n ) + η x i ( n ) y j ( n ) ∑ i [ w j i ( n ) + η x i ( n ) y j ( n ) ] 2 w_{ji}(n + 1) = \frac{w_{ji}(n) + \eta x_i(n)y_j(n)}{\sqrt{\sum_i[w_{ji}(n) + \eta x_i(n)y_j(n)]^2}} wji(n+1)=∑i[wji(n)+ηxi(n)yj(n)]2 wji(n)+ηxi(n)yj(n)
Oja 提出，对于小的学习率 η η η（ η < < 1 η<<1 η<<1），上述归一化可以近似为：
w j i ( n + 1 ) = w j i ( n ) + η y j ( n ) [ x i ( n ) − y j ( n ) w j i ( n ) ] w_{ji}(n + 1) = w_{ji}(n) + \eta y_j(n) [x_i(n) - y_j(n)w_{ji}(n)] wji(n+1)=wji(n)+ηyj(n)[xi(n)−yj(n)wji(n)]
这是 Oja's Rule，或归一化的赫布学习规则。它涉及一个"遗忘项"（ − y j ( n ) w j i ( n ) - y_j(n)w_{ji}(n) −yj(n)wji(n)），防止权重无界增长。
通过李雅普诺夫（Lyapunov）函数分析，已经证明Oja's Rule是渐近收敛的。这意味着随着时间的推移，使用奥贾规则训练的神经网络的权重会收敛到一个稳定的解，这与赫布学习规则不同，后者本质上是不稳定的。
Oja's Rule在输入空间中创建了一个主成分，当应用于单个神经元时，权重向量会捕捉输入数据中最重要的特征或模式。
那么问题现在在于如何找到输入空间中具有显著方差的其他成分。
这需要我们将数据投影到正交的方向上。
一种常见的方法是从输入数据中减去主成分。通过这种方式，我们可以消除数据中与主成分相关的部分，从而得到正交方向上的投影。（放缩，deflation）
奥贾规则不仅可以用于提取第一个主成分，还可以扩展到提取多个主成分。这意味着我们可以依次找到数据中的多个重要方向，并在这些方向上进行投影，从而捕获更多的信息。
当然降维也可以解决这个问题。
3.2.1 放缩（Deflation）
我们现在重点说一下刚刚提到的放缩（deflation）。
奥贾规则（Oja's Rule）在提取主成分（特征向量）时，可以采用一种叫做"放缩"（deflation）的过程来计算其他的特征向量。
假设第一个主成分（即具有最大特征值的特征向量）已经被找到。
计算第一个特征向量（即具有最大特征值的特征向量） w 1 \mathbf{w}1 w1在输入 x \mathbf{x} x上的投影：
proj w 1 x = w 1 T x \text{proj}{\mathbf{w}_1} \mathbf{x} = \mathbf{w}_1^T \mathbf{x} projw1x=w1Tx
这一步的目的是量化输入数据在第一个主成分方向上的分量。
从原始输入数据中减去其在第一个特征向量上的投影，生成修改后的输入数据 x ^ \hat{\mathbf{x}} x^：
x ^ = x − proj w 1 x = x − w 1 ( w 1 T x ) \hat{\mathbf{x}} = \mathbf{x} - \text{proj}_{\mathbf{w}_1} \mathbf{x} = \mathbf{x} - \mathbf{w}_1 (\mathbf{w}_1^T \mathbf{x}) x^=x−projw1x=x−w1(w1Tx)
这样，修改后的输入数据不再包含第一个主成分的信息。
然后在修改后的数据 x ^ \hat{\mathbf{x}} x^上重复应用奥贾规则，以找到下一个主成分（即第二大的特征值对应的特征向量）。
3.3 主成分分析（PCA）在神经网络中的应用
在神经网络中应用PCA可以帮助网络学习到数据中最重要的特征，同时减少模型的复杂度。
将选定的主成分特征向量用作权重矩阵 W L W_L WL的列。这样， W L W_L WL就反映了数据的主成分方向。
W L W_L WL作为连接输入层和瓶颈层之间的权重矩阵。瓶颈层通过这些权重将高维数据映射到低维空间，从而实现降维。
多层网络包含多个隐藏层，而瓶颈层（bottleneck layer）是网络中神经元数量最少的层，其目的是减少网络的参数数量，从而降低模型复杂度并防止过拟合。
网络使用自联想输出进行训练，即输入和输出相同（ e = x − y e=x−y e=x−y）。这种训练方式有助于网络学习到数据的内在结构和特征。
W L W_L WL表示从输入层到瓶颈层的权重矩阵，它捕捉了输入数据中最重要的特征或模式。
W L W_L WL跨越了前 m m m个主成分特征向量所构成的子空间，捕捉了数据中最重要的 m m m个方向，这些方向代表了数据中的主要变异性。
下图更详细介绍了这个过程。
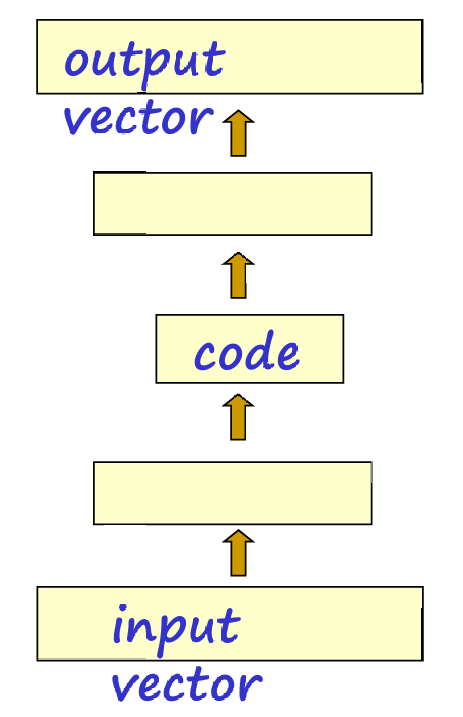
使用反向传播（back-propagation）算法进行无监督学习。
网络设计中包含一个瓶颈层，该层的神经元数量少于输入层和输出层。瓶颈层有助于提取输入数据的高效表示（即特征）。
训练目标是使网络的输出与输入相同。这种自联想学习（auto-associative learning）方法有助于网络学习到输入数据的压缩表示。
瓶颈层中的隐藏单元活动形成了一个高效编码。这意味着瓶颈层能够捕获输入数据中最重要的特征，并且去除冗余信息。
瓶颈层有助于提取独立特征，即瓶颈层不包含冗余特征，而是尽可能地保留数据的关键信息。
输入向量（input vector）通过一系列权重（ W L W_L WL）被映射到瓶颈层，形成编码（code）。编码进一步被映射到输出向量（output vector），目标是使其与原始输入向量相同。
3.4 自编码器（autoencoder）
反向传播算法可以用于无监督学习，以发现能够描述输入模式的重要特征。
这通过学习输入数据到自身的映射（即输入和输出相同），可以实现数据的压缩和特征提取。自编码器包含一个瓶颈层，该层的神经元数量少于输入和输出层，从而实现降维。
数据首先通过编码器被压缩成瓶颈层的低维表示（即压缩数据），然后通过解码器恢复到原始维度（即解压数据）。
这种通过学习输入数据到自身的映射来实现数据的压缩和特征提取的叫做自编码器。
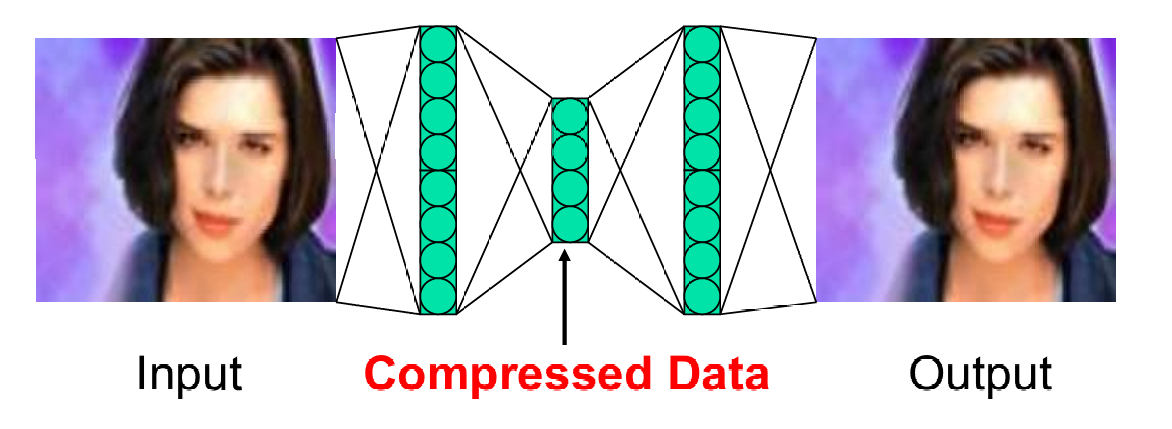
自编码器是一种前馈神经网络，它学习将输入数据映射到自身。换句话说，自编码器的目标是让网络的输出尽可能接近于输入，即 y ( i ) = x ( i ) y^{(i)}=x^{(i)} y(i)=x(i)。
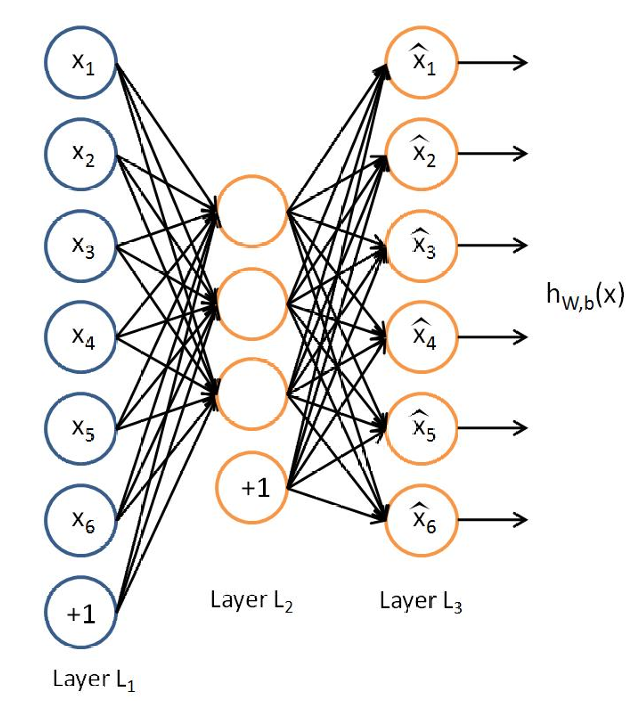
编码器（Encoder）：
编码器是自编码器的前半部分，它负责将输入数据压缩成一个低维的表示，通常称为"潜在空间"或"瓶颈层"。
编码器通过学习输入数据的紧凑表示来捕获数据中最重要的特征。
解码器（Decoder）：
解码器是自编码器的后半部分，它负责将编码器的输出（低维表示）恢复到原始数据的维度。
解码器尝试重建原始输入数据，从而实现数据的解压。
自编码器的目标是在输出层重现输入数据的模式。
自编码器可以包含不同数量的隐藏层，每层的神经元数量也可以不同。这种灵活性允许自编码器适应不同类型的数据和任务。
自编码器倾向于找到一个类似于PCA的数据描述。
自编码器中的瓶颈层（bottleneck layer）是神经元数量最少的层。瓶颈层的作用是压缩数据，即提取数据的关键特征。
瓶颈层中的少量神经元起到信息压缩器（或编码器）的作用，它们能够捕获数据中最重要的信息，并去除冗余。
因此这里将其与PCA进行对比：
PCA 是一种常用的降维技术，它通过找到数据中最重要的方向（主成分）来简化数据表示。
自编码器在某种程度上与PCA相似，因为它也试图在低维空间中捕获数据的主要特征。
然而，自编码器是一种非线性模型，它可以通过学习非线性关系来更好地捕获数据的特征。
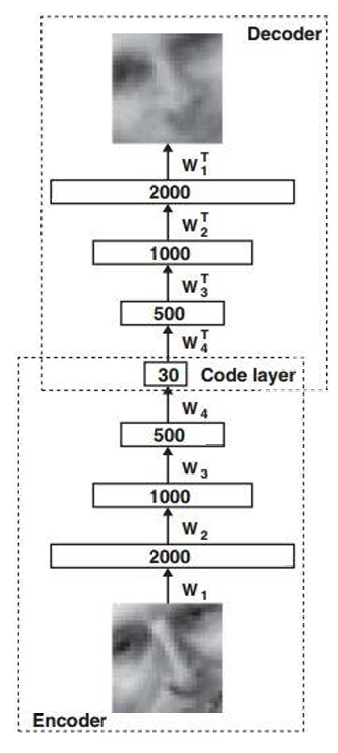
3.4.1 深度自编码器（Deep Auto-encoder）
深度自编码器是一种通过扩展自编码器的编码器和解码器，加入多个隐藏层来构建的神经网络结构。
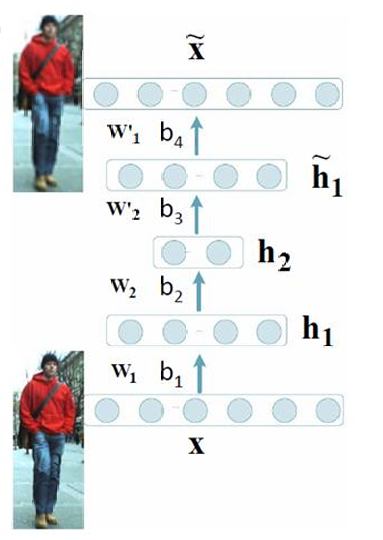
3.4.2 去噪自编码器（Denoising Auto-encoder）
去噪自编码器通过向输入数据添加随机噪声来训练模型。这样做的目的是迫使自编码器学习到更鲁棒的特征，即那些即使在输入数据受到干扰时也能保持稳定的特征。
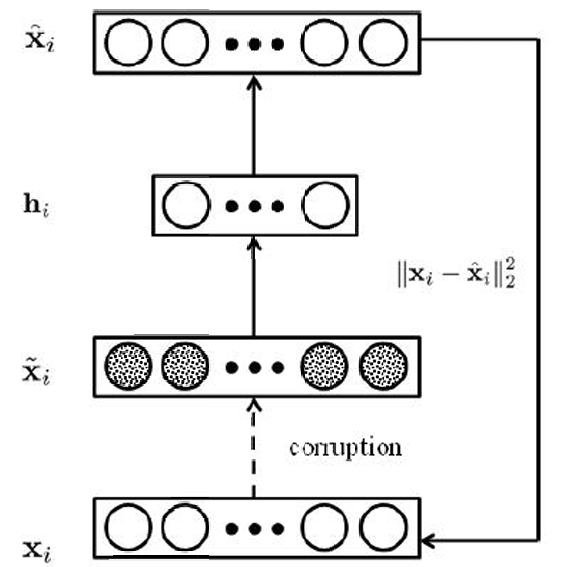
去噪自编码器的训练涉及到最小化一个损失函数，该函数衡量了原始输入数据和自编码器输出之间的差异。
损失函数包括两个部分：误差与正则化项，如下文所示。
编码过程：
h ( ℓ ) = σ ( W 1 x ~ ( ℓ ) + b 1 ) h^{(\ell)} = \sigma(\mathbf{W}_1 \tilde{\mathbf{x}}^{(\ell)} + \mathbf{b}_1) h(ℓ)=σ(W1x~(ℓ)+b1)
解码过程：
x ^ ( ℓ ) = σ ( W 2 h ( ℓ ) + b 2 ) \hat{\mathbf{x}}^{(\ell)} = \sigma(\mathbf{W}_2 h^{(\ell)} + \mathbf{b}_2) x^(ℓ)=σ(W2h(ℓ)+b2)
损失函数：
min W 1 , W 2 , b 1 , b 2 ∑ ℓ ∥ x ( ℓ ) − x ^ ( ℓ ) ∥ 2 2 + λ ( ∥ W 1 ∥ F 2 + ∣ W 2 ∥ F 2 ) \min_{\mathbf{W}_1, \mathbf{W}_2, \mathbf{b}_1, \mathbf{b}2} \sum{\ell} \|\mathbf{x}^{(\ell)} - \hat{\mathbf{x}}^{(\ell)}\|_2^2 + \lambda(\|\mathbf{W}_1\|_F^2 + |\mathbf{W}_2\|_F^2) minW1,W2,b1,b2∑ℓ∥x(ℓ)−x^(ℓ)∥22+λ(∥W1∥F2+∣W2∥F2)
其中， σ σ σ是激活函数， W 1 W_1 W1, W 2 W_2 W2是权重矩阵， b 1 b_1 b1, b 2 b_2 b2是偏置向量， λ λ λ是正则化参数， ∣ ⋅ ∣ F ∣⋅∣_F ∣⋅∣F表示Frobenius范数。
3.4.3 自编码器网络（Auto-encoders Network）
自编码器网络的目标是使其输出尽可能地接近输入数据。在自编码器中，输入数据首先被编码成一个短编码，这个编码位于隐藏层中。隐藏层中的编码保留了关于输入数据的最大信息量，尽管维度更小。然后，网络尝试从隐藏层的编码重建输入数据，即解码过程。
3.5 聚类分析（Clustering Analysis）
聚类分析是一种将数据集划分为多个簇的过程。这个过程不依赖于预先定义的标签或类别，而是根据数据点之间的相似性来分组。
这一部分在前面第六章讲过。相关资料
一个簇（Cluster）是数据点的集合，其中每个观测值与其他同簇中的观测值相似，而与其他簇中的观测值不相似。
在同一簇中，数据点彼此之间具有较高的相似性，这种相似性可以根据不同的标准来定义，如距离、密度或连接性等。
不同簇之间的数据点具有较低的相似性，意味着它们在某些特征上存在显著差异。
聚类分析通过抽象数据的潜在结构来组织数据。这种结构可以表现为个体的分组，或者群体的层次结构。
聚类中的分组是基于模式之间的测量或感知相似性。因此聚类是一种无监督学习方法。
在应用上：
- 聚类可以作为一个独立的工具来使用，帮助我们理解数据的分布情况，揭示数据中的潜在结构和模式。
- 也可以作为其他算法的预处理步骤。例如，在应用某些机器学习算法之前，聚类可以帮助减少数据的维度，去除噪声，或将数据转换为更适合算法处理的形式。
3.5.1 K-means算法
k-means 算法将整个数据集划分为 k k k个簇，其中每个簇包含一组数据点，这些数据点在某种程度上彼此相似。而这些簇是互斥的，意味着每个数据点只能属于一个簇。没有数据点可以同时属于多个簇。
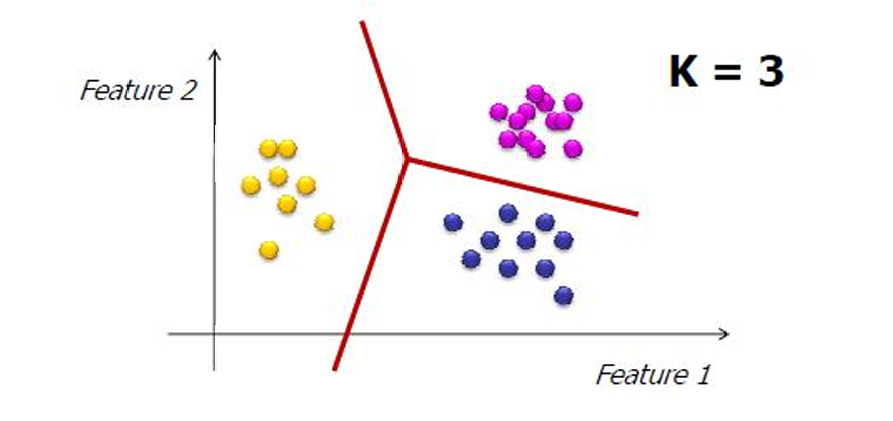
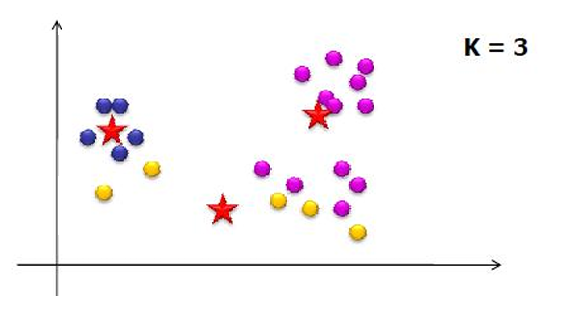
k-means 算法的目标是最小化每个簇中所有点到其"代表性对象"（即簇中心或质心）的平方距离之和。
这里的数学表达式为：
∑ i = 1 K ∑ x j ∈ S i d 2 ( x j , μ i ) \sum_{i=1}^{K} \sum_{x_j \in S_i} d^2(x_j, \mu_i) ∑i=1K∑xj∈Sid2(xj,μi)
其中， S i S_i Si是第 i 个簇， i = 1 , 2 , ... , K i=1,2,...,K i=1,2,...,K。
μ i \mu_i μi是第 i i i个簇中所有点的质心（centroid），即簇中所有点的平均位置。
d d d是距离函数，通常在 k-means 算法中使用欧几里得距离。
k-means 算法的基本目标是找到数据集的最紧凑的划分方式，将数据集划分为 k 个互斥的簇（partitions）。
算法试图最小化每个簇内部数据点之间的方差，即簇内数据点的紧密程度。同时，算法试图最大化不同簇之间的方差，即不同簇之间的数据点尽可能分散。
如果我们事先知道每个数据点的簇分配，那么我们可以直接计算每个簇的质心（centroid）位置。如果我们事先知道质心的位置，那么我们就可以很容易地将每个数据点分配到最近的簇。
但实际情况是，我们通常既不知道数据点的簇分配，也不知道质心的位置。这是 k-means 算法需要解决的核心问题。
算法步骤如下：
- 选择簇的数量 (K)：
首先，需要确定要将数据集划分成多少个簇（即 k 值）。 - 随机选择初始质心位置：
随机选择 k 个数据点作为初始的质心（centroids）的位置。这些质心是每个簇的代表点，算法将围绕这些点迭代优化簇的划分。 - 分配数据点到最近的质心：
将每个数据点分配到最近的质心。这一步依赖于选择的距离度量，常用的是欧氏距离。每个数据点根据到各个质心的距离被分配到最近的簇。 - 重新计算质心位置：
一旦所有点被分配完毕，就重新计算每个簇的质心，通常是簇中所有点的平均位置。 - 检查收敛：
重复步骤 3 和 4，直到质心的位置不再显著变化，或者达到一定的迭代次数，算法停止。这表明算法已经收敛到一个稳定的解。
在聚类问题中，最优解通常指的是能够最小化簇内方差（即簇内数据点的紧密程度）和最大化簇间方差（即簇间数据点的分散程度）的划分。
因此k-means算法有其局限性：
- 对初始质心敏感：k-means 算法的结果可能依赖于初始质心的选择，不同的初始质心可能导致不同的聚类结果。
- 局部最优而非全局最优：k-means 算法可能只收敛到局部最优解，而不是全局最优解。这是因为算法通过迭代优化逐步改进聚类，但可能在迭代过程中陷入局部最小值。
对于这些问题可以： - 多次运行：可以通过多次运行 k-means 算法，每次使用不同的初始质心，然后选择最佳的聚类结果来缓解这个问题。
- 使用其他聚类算法：考虑使用其他聚类算法，如层次聚类或基于密度的聚类算法，这些算法可能提供不同的聚类结果。
- 后处理技术：使用后处理技术（如轮廓系数，silhouette score）来评估聚类的质量，帮助识别和改进次优解。
3.6 无监督竞争学习（Unsupervised Competitive Learning）
在赫布网络（Hebbian networks）中，所有神经元可以同时"激活"（即发放动作电位）。
竞争学习是一种无监督学习机制，其中每个时间步只有每个神经元组中的一个神经元可以"激活"（即发放动作电位）。
输出单元（即网络的输出层神经元）相互竞争，以决定哪个单元最终被激活。
竞争对于神经网络来说非常重要，因为它有助于网络学习区分不同的输入模式，并提高网络对特定输入的响应能力。
在生物神经系统中，神经元之间的竞争已被观察到，它有助于大脑处理信息和执行复杂任务。
在生物神经系统中，神经元之间的竞争是常见的现象，它有助于大脑有效地处理和响应外部刺激。
将输入模式分类到 m m m个类别中的一个。
在理想情况下，只有一个节点（或输出单元）给出输出 1，所有其他节点的输出都是 0。
通常，会有多个节点有非零输出，这意味着多个类别节点竞争以对输入数据进行分类。
类别节点相互竞争，最终可能只有一个节点胜出，其他节点"失败"（即输出为 0）。胜出的节点代表计算出的输入的分类结果。
3.6.1 无监督竞争学习的结构
在图中，活跃（active）或非活跃（inactive）的单位用点表示。
活跃的单位用实心点（filled dots）表示，非活跃的单位用空心点（open dots）表示。
给定层中的一个单位可以从下一个较低层的所有单位接收输入。
它可以将输出投射到下一个较高层的所有单位。
层与层之间的连接是兴奋性的（excitatory），这意味着来自较低层的信号可以激活较高层的单位。
层内的连接是抑制性的（inhibitory），每个层由一组相互抑制的簇组成。
簇内的单位相互抑制，以确保每个簇中只有一个单位可以活跃。
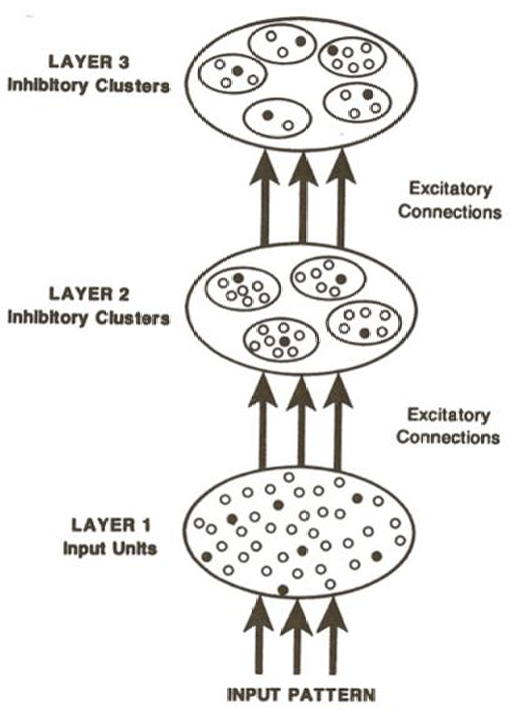
如上图所示。图中展示了一个三层神经网络的结构。
第一层（Layer 1）：输入单元，接收输入模式。
第二层（Layer 2）：抑制簇，每个簇中的单元相互抑制。
第三层（Layer 3）：抑制簇，进一步处理来自第二层的输出。
3.6.2 赢者通吃（Winner-takes-all， WTA）
在所有竞争的节点中，只有获胜的一个节点会被激活（即输出为 1），而其他所有节点的输出都将是 0。这意味着在每个时间步，只有一个节点能够"赢得"竞争并响应输入数据。、这种机制的目的是确保网络中的每个输入模式只由一个节点来表示，从而实现数据的有效编码和特征提取。
最简单的实现 WTA 机制的方法是有一个外部的、中心的仲裁者（例如一个程序）来决定胜者。这个仲裁者通过比较竞争节点（即网络中的神经元）的当前输出来决定胜者，以打破平局。
这里提到的方法在生物学上是不切实际的，因为在生物神经系统中不存在这样的外部仲裁者。
3.6.3 简单竞争学习（Simple Competitive Learning）
简单竞争学习是一种无监督学习方法，用于模式识别和聚类。具体步骤如下：
- 初始化原型向量（Prototype Vectors）：
首先，需要初始化 K K K个原型向量，这些向量代表 K K K个不同的类别或簇。 - 呈现单个样本（Present a Single Example）：
然后，逐个呈现数据集中的样本。 - 识别最近的原型（Identify the Closest Prototype）：
对于每个样本，算法需要识别与其最接近的原型，即找到所谓的"胜者"（winner）。 - 移动胜者（Move the Winner）：
接着，将胜者原型向量向样本移动，使其更接近该样本。
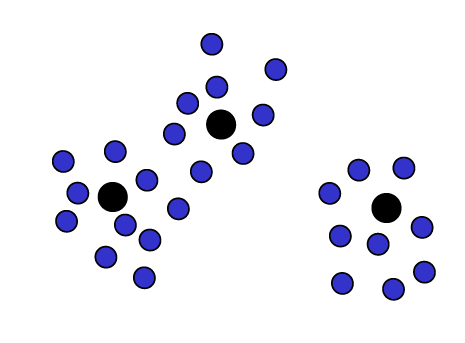
这个过程直观且合理，因为它将原型放置在数据密度较高的区域，从而更好地表示数据中的模式。
它还能识别出特征的最重要组合，有助于发现数据中的结构和模式。
那这里的胜者是怎么定义的呢？
对于每个输出节点 j j j，计算其激活值 h j h_j hj:
h j = ∑ i w j i x i h_j=\sum_{i} w_{ji} x_i hj=∑iwjixi
其中 w j i w_{ji} wji是从输入节点 i i i到输出节点 j j j的权重， x i x_i xi是输入向量的第 i i i个分量。
胜者是激活值最大的输出节点，即：
w j ∗ ⋅ x ≥ w j ⋅ x ∀ x w_{j^*} \cdot x \geq w_j \cdot x \quad \forall x wj∗⋅x≥wj⋅x∀x
胜者也可以理解为与输入向量 x 的欧几里得距离（Euclidean distance）最近的输出节点。
除此之外还有侧抑制（Lateral Inhibition）。它指的是网络中一个节点的激活会抑制其他节点的激活。这种机制有助于确保在任何给定时间步，只有一个节点能够成为胜者。
我们现在介绍更新规则，用于调整神经网络中的权重。
对于每个神经元，权重的更新规则为： Δ w j ∗ i = η y j ( x i − w j ∗ i ) \Delta w_{j^*i} = \eta y_j (x_i - w_{j^*i}) Δwj∗i=ηyj(xi−wj∗i)。
其中， Δ w j ∗ i \Delta w_{j^*i} Δwj∗i是第 j ∗ j^* j∗个胜者神经元的第 i i i个权重的变化量。
η \eta η是学习率。
y j y_j yj是第 j j j个神经元的激活值。
x i x_i xi是输入向量的第 i i i个分量。
w j ∗ i w_{j^*i} wj∗i是第 j ∗ j^* j∗个胜者神经元的第 i i i个权重。
激活值定义为：
y j ∗ = { 1 if j = j ∗ 0 if j ≠ j ∗ y_{j^*} = \begin{cases} 1 & \text{if } j = j^* \\ 0 & \text{if } j \neq j^* \end{cases} yj∗={10if j=j∗if j=j∗
y j ∗ = 1 y_{j^*} = 1 yj∗=1表示胜者节点的激活值。
y j = 0 y_j = 0 yj=0表示非胜者节点的激活值。
只有胜者节点的输入权重会被修改。
一些单元可能永远不会或很少成为胜者，因此权重向量可能不会被更新，导致"死亡单元"（Dead Unit）。
因此简单竞争学习的目标是使每个输出单元（或节点）移动到输入向量簇的质心，从而实现聚类。
在简单竞争学习中，每个输出单元会根据输入向量的位置进行调整，以便更好地代表输入数据的分布。
这个过程涉及到将输出单元移动到输入向量簇的中心位置，从而形成聚类。
左图：初始状态，输出单元（星形标记）分布在输入向量（黑色点）的不同位置。
中图：中间状态，输出单元开始向输入向量的簇中心移动。
右图：最终状态，输出单元已经移动到输入向量簇的中心，形成清晰的聚类。
3.6.3.1 公平竞争（Enforcing Fairer Competition）
输出单元的权重向量的初始位置可能位于数据模式稀少的区域。
输出单元的权重向量的初始位置可能位于数据模式稀少的区域。
为了更有效地确保公平竞争，每个单元应该都有平等的机会来代表训练数据的一部分。
这样可以避免某些单元因为初始位置不佳而无法更新其权重，从而无法学习到数据中的重要模式。
3.6.3.2 漏斗学习（Leaky Learning）
因此我们介绍漏斗学习（Leaky Learning），这是对于这种死亡单元问题的一种解决方法。
漏斗学习是一种改进的竞争学习规则，它允许网络中的所有单元（无论是胜者还是败者）都有机会更新其权重，但更新的速率不同。这种方法旨在确保每个单元都能在一定程度上学习到数据中的模式，从而避免某些单元因从未成为胜者而停止学习。
因此权重更新规则不仅影响胜者（即对输入模式响应最大的单元），也影响败者（即对输入模式响应较小的单元）。
权重更新规则为：
w ( t + 1 ) = w ( t ) + { η w ( x − w ( t ) ) if the unit is a winner η L ( x − w ( t ) ) if the unit is a loser w(t + 1) = w(t) + \begin{cases} \eta_w (x - w(t)) & \text{if the unit is a winner} \\ \eta_L (x - w(t)) & \text{if the unit is a loser} \end{cases} w(t+1)=w(t)+{ηw(x−w(t))ηL(x−w(t))if the unit is a winnerif the unit is a loser
其中：
w ( t ) w(t) w(t)是当前时刻的权重向量。
x x x是输入向量。
η w \eta_w ηw是胜者的学习率。
η L \eta_L ηL是败者的学习率。
η w ≫ η L \eta_w \gg \eta_L ηw≫ηL表示胜者的学习率大于败者的学习率。
这种更新机制的效果是慢慢地将败者的权重向量移动到数据模式空间中更密集的区域，从而提高网络的整体学习能力和泛化能力。
下图展示了一个例子。
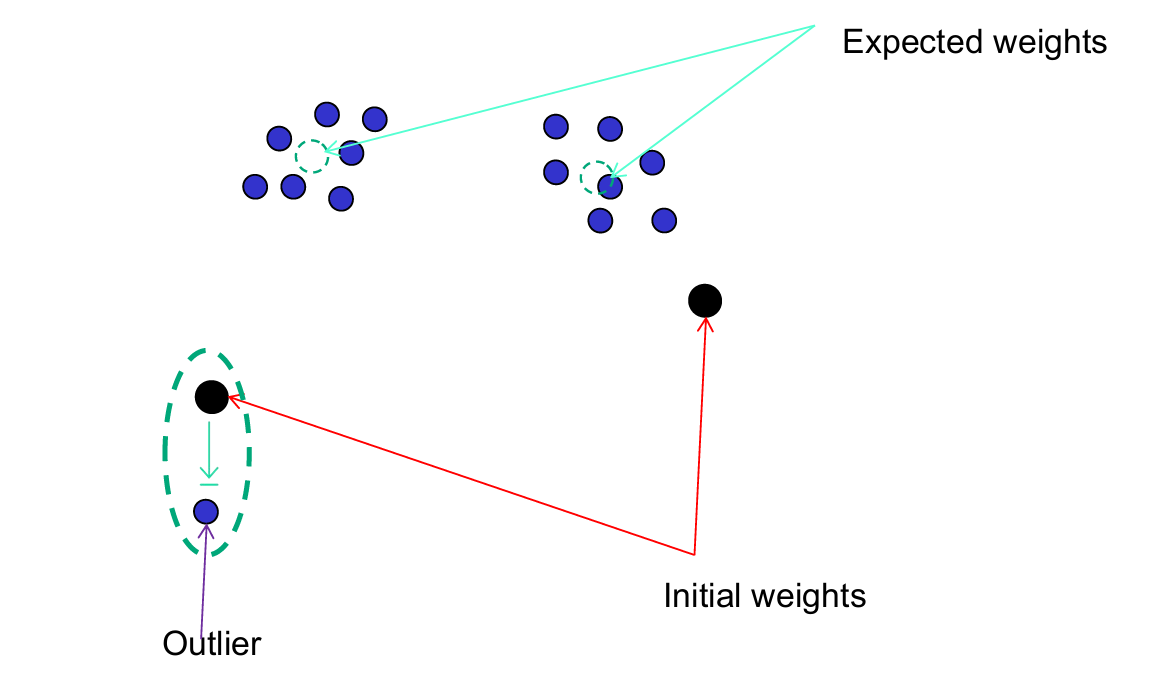
其初始权重向量（红色箭头）位于数据模式稀少的区域。
期望权重向量（青色箭头）表示如果权重能够正确更新，该单元应该位于的位置，以便更好地捕捉数据的主要模式。
通过漏斗学习，单元逐渐移动到数据点更密集的区域。