机器学习中的决策树算法是一种直观且强大的工具,它模拟人类决策过程,通过树状结构对数据进行分类或回归预测。本文将深入探讨决策树的基础概念、经典算法、过拟合问题及解决方案,以及实际应用中的扩展处理。
一、决策树学习基础
适用场景
决策树特别适合以下类型的问题:
-
带有非数值特征的分类问题
-
离散特征
-
没有明确相似度概念的数据
-
特征无序的数据集
样本表示
决策树处理的是属性列表而非数值向量。例如:
-
例如享受运动的例子:{天气=晴, 温度=暖, 湿度=一般, 风=强, 水温=暖, 预测天气=不变}
-
例如水果的例子:{颜色=红, 大小=小, 形状=球形, 味道=甜}
训练数据通常以多条属性记录的形式存在,例如:
-
<香蕉>: 黄色、细长、中、甜 -
<西瓜>: 绿色、球形、大、甜
训练样本
| Sky (天气) | Temp (温度) | Humid (湿度) | Wind (风) | Water (水) | Forecast (预测天气) | Enjoy (享受与否) |
|---|---|---|---|---|---|---|
| Sunny | Warm | Normal | Strong | Warm | Same | Yes |
| Sunny | Warm | Hign | Strong | Warm | Same | Yes |
| Rainy | Cold | Hign | Strong | Warm | Change | No |
| Sunny | Warm | Hign | Strong | Cold | Change | Yes |
- <香蕉>:黄色、细长、中、甜
- <西瓜>:绿色、球形、大、甜
- <香蕉>:黄色、细长、中、甜
- <葡萄>:绿色、球形、小、甜
- <葡萄>:红色、球形、小、酸
决策树概念
决策树是一种树形结构,其中:
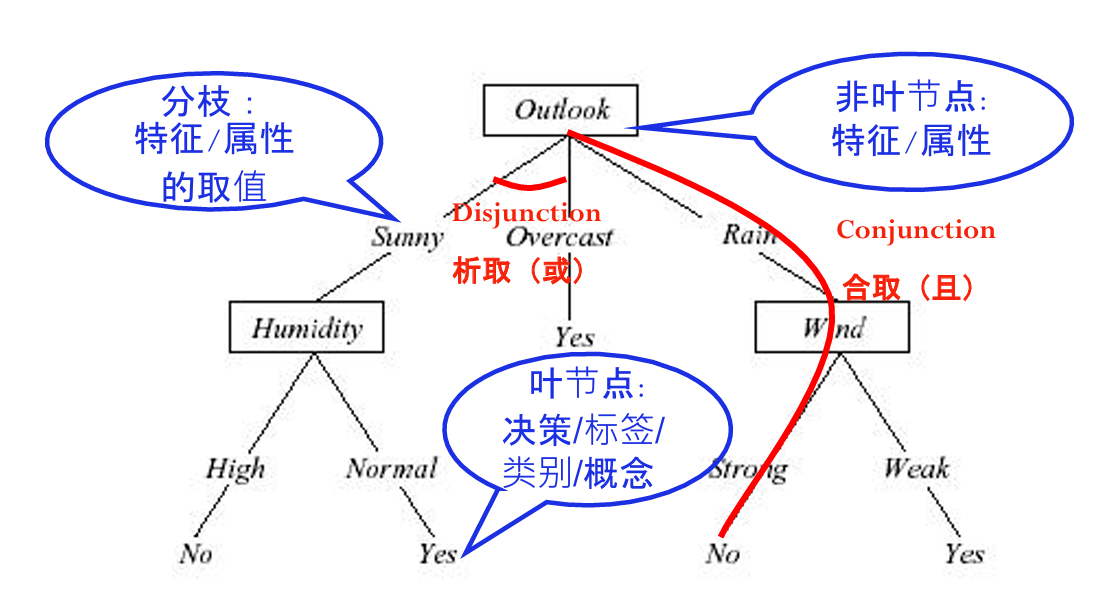
-
非叶节点代表特征/属性
-
分支代表该叶子节点特征/属性的取值
-
叶节点代表决策/标签/类别/概念
关系
- 从根节点到叶节点,是且的关系。如天气下雨,并且风力很强,就No
- 同一个节点下面不同分支,是或的关系。 比如天气时晴天、或者阴天、或者雨天
决策树发展历程
决策树算法自1966年由Hunt首次提出后,经历了多次重要发展:
-
1970-1980年代:CART(由Friedman和Breiman提出)和ID3(由Quinlan提出)算法问世
-
1990年代以来:算法改进和对比研究广泛开展
-
1993年:Quinlan提出C4.5算法,成为最广泛使用的决策树算法之一
二、经典决策树算法:ID3
ID3算法采用自顶向下的贪心搜索策略,通过递归方式构建决策树。其核心循环包括:
-
选择下一步最佳决策属性
-
将该属性作为当前节点的决策属性
-
为属性的每个值创建对应的新子节点
-
根据属性值将训练样本分配到各个节点
-
如果训练样本被完美分类则停止,否则继续分裂
Q1, 哪个属性是最佳属性?
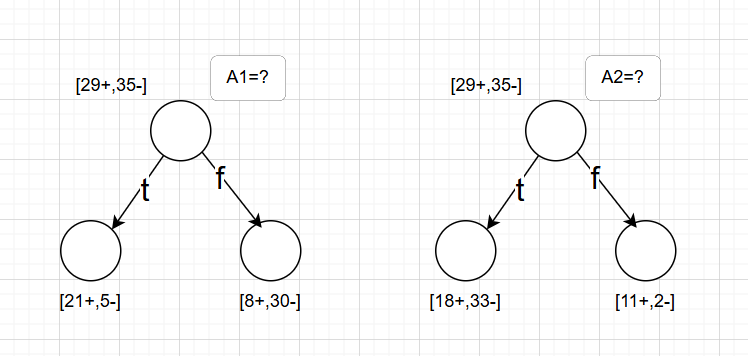
- 一共有64个数据, 其中29个正例,35个负例
- 以A1来区分,属于True的有21正5负, 属于负的有8正30负
- 以A2来区分,属于True的有18正33负,属于负的有11正2负
- A1和A2哪个属性为最佳属性呢?
属性选择与节点混杂度
ID3算法的关键在于如何选择最佳分裂属性。算法倾向于选择简洁的、节点数较少的树,即在每个节点上选择能使数据尽可能"纯"的属性。
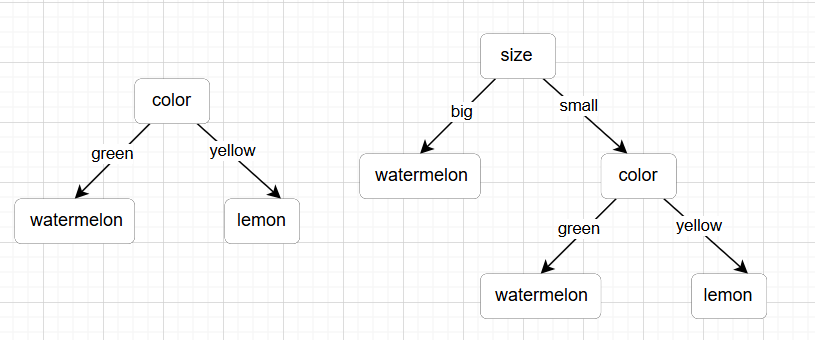
- 左边根据颜色判断是watermelon还是lemon
- 右边会先根据大小判断,大的是watermelon。小的再根据颜色来判断
- 所以认为左边的更加简洁,更好
如何衡量混杂度?
混杂度(impurity)衡量指标包括:
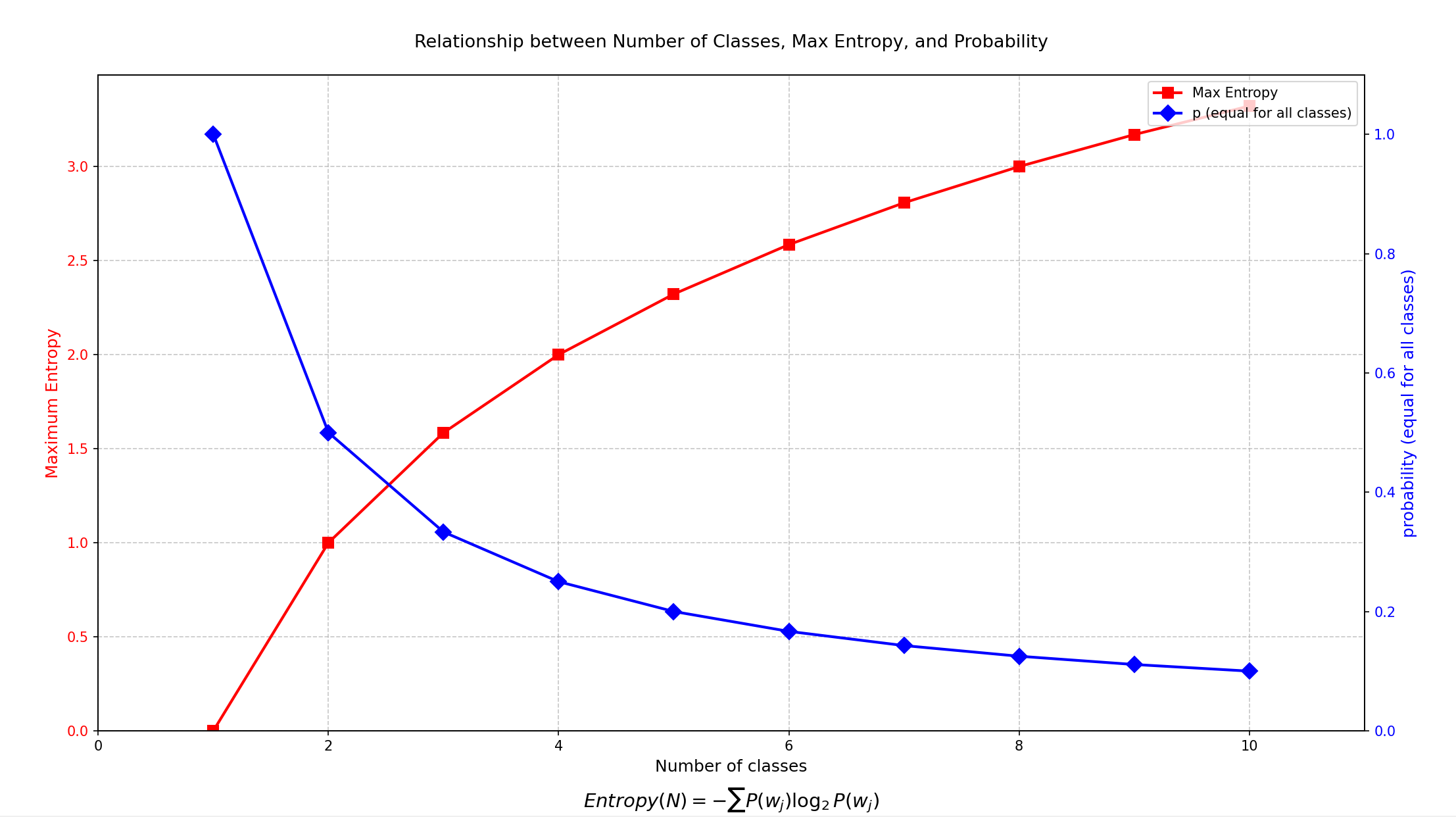
- 熵(Entropy) :Entropy(N)=−∑jP(wj)log2P(wj)Entropy(N)=-\sum_j P(w_j)\log_2 P(w_j)Entropy(N)=−∑jP(wj)log2P(wj)
- 定义: 0log0 = 0
- 熵度量了信息的不确定性
- 正态分布具有最大熵值。
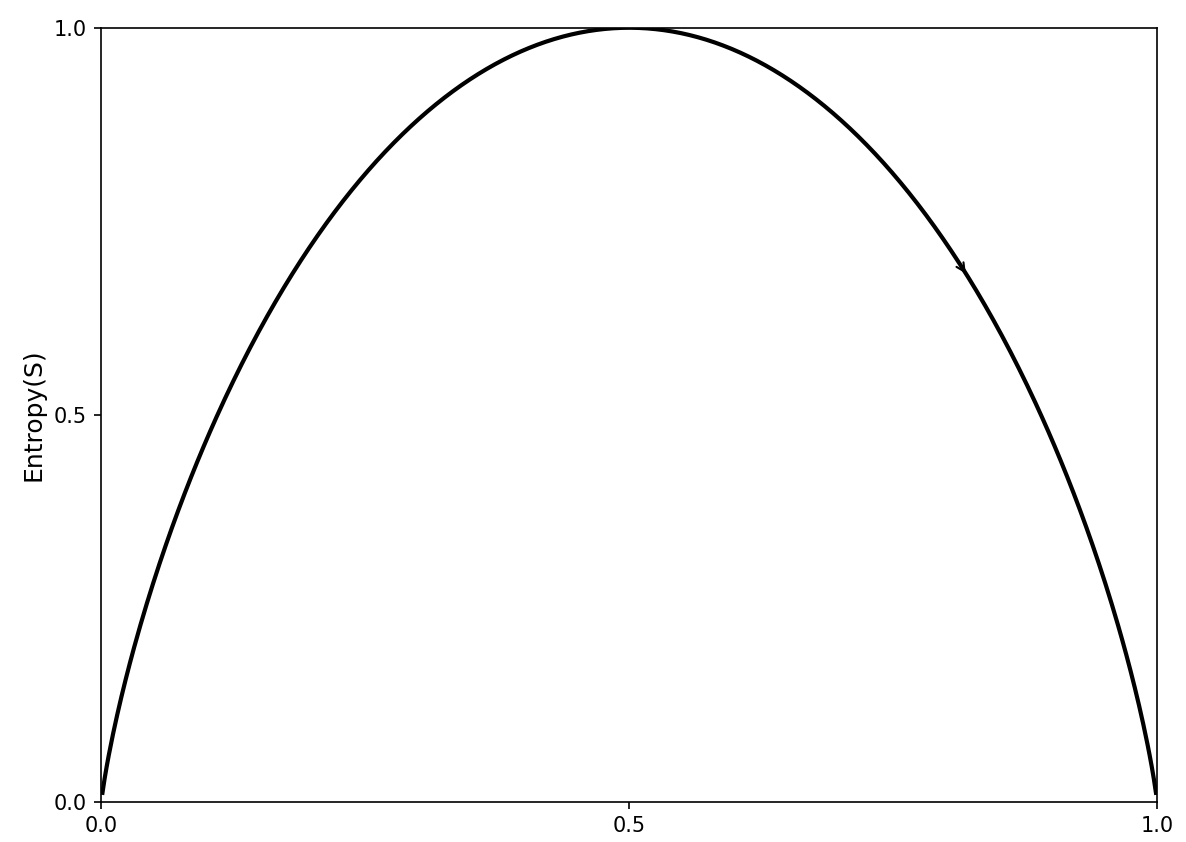
按上面例子,计算熵值:
Entropy(S)=−2964∗log22964−3564∗log23564=0.993 Entropy(S) = -\frac{29}{64}*log_2\frac{29}{64}-\frac{35}{64}*log_2\frac{35}{64} = 0.993 Entropy(S)=−6429∗log26429−6435∗log26435=0.993
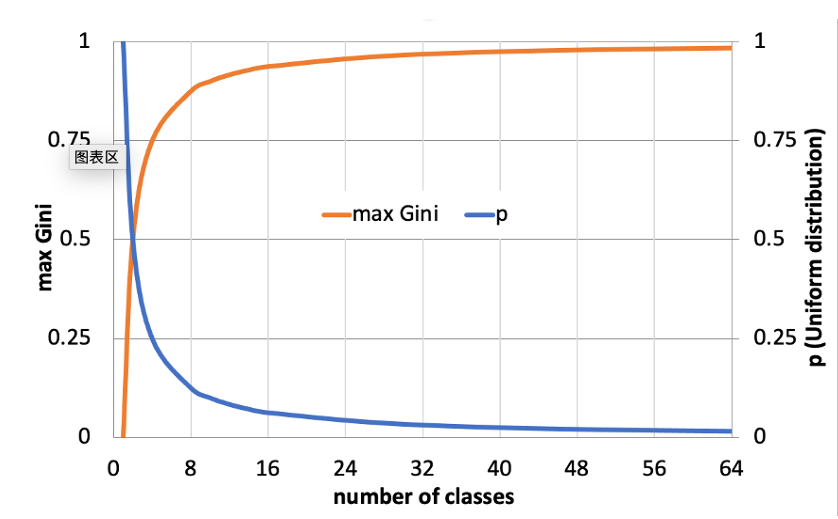
- Gini混杂度 :i(N)=∑i≠jP(wi)P(wj)=1−∑jP2(wj)i(N)=\sum_{i\neq j}P(w_i)P(w_j)=1-\sum_j P^2(w_j)i(N)=∑i=jP(wi)P(wj)=1−∑jP2(wj)
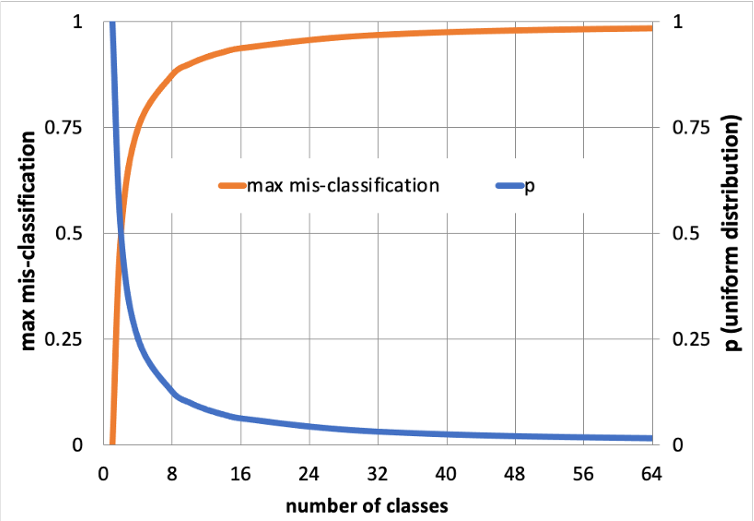
- 错分类混杂度 :i(N)=1−maxjP(wj)i(N)=1-\max_j P(w_j)i(N)=1−maxjP(wj)
度量混杂度的变化ΔI(I)-信息增益(Information Gain)
信息增益是选择分裂属性的核心指标,表示因属性排序整理带来的熵的期望减少量。通过计算每个属性的信息增益,可以选择最能减少不确定性的属性。
Gain(S,A)≡Entropy(S)−∑v∈Values(A)∣Sv∣∣S∣Entropy(Sv) \text{Gain}(S,A)\equiv \text{Entropy}(S)-\sum_{v\in \text{Values}(A)}\frac{|S_v|}{|S|}\text{Entropy}(S_v) Gain(S,A)≡Entropy(S)−v∈Values(A)∑∣S∣∣Sv∣Entropy(Sv)

计算信息增益:
- 原始熵为Entropy(S)=−2964∗log22964−3564∗log23564=0.993Entropy(S) = -\frac{29}{64}*log_2\frac{29}{64}-\frac{35}{64}*log_2\frac{35}{64} = 0.993Entropy(S)=−6429∗log26429−6435∗log26435=0.993
- 经过A1属性排序整理, Entropy(SA1=t)=0.706,Entropy(SA1=f)=0.742Entropy(S_{A1=t})=0.706,Entropy(S_{A1=f})=0.742Entropy(SA1=t)=0.706,Entropy(SA1=f)=0.742
- Gain(S,A1)=0.993−(2664∗0.706+3864∗0.742)=0.266\text{Gain}(S,A_1)=0.993-(\frac{26}{64}*0.706+\frac{38}{64}*0.742)=0.266Gain(S,A1)=0.993−(6426∗0.706+6438∗0.742)=0.266
- 经过A2属性排序整理, Entropy(SA2=t)=0.936,Entropy(SA2=f)=0.619Entropy(S_{A2=t})=0.936,Entropy(S_{A2=f})=0.619Entropy(SA2=t)=0.936,Entropy(SA2=f)=0.619
- Gain(S,A2)=0.993−(5164∗0.936+1364∗0.619)=0.121\text{Gain}(S,A_2)=0.993-(\frac{51}{64}*0.936+\frac{13}{64}*0.619)=0.121Gain(S,A2)=0.993−(6451∗0.936+6413∗0.619)=0.121
- 因此,对A1属性排序整理信息增益较大, A1为最佳属性
Q2, 何时返回(停止分裂节点)?
终止条件
ID3算法在以下两种情况停止分裂:
-
第一种情况, 当前子集中所有数据有完全相同的输出类别
- 例如享受运动的例子,都选择去或者选择不去
-
第二种情况,当前子集中所有数据有完全相同的输入特征值
- 例如享受运动的例子,虽然有人选择去有人选择不去, 但是天气完全一样(输入完全相同),那也不用再分裂了
- 可能1: 有噪声;可能二: 有重要特征被漏掉了
是否存在第三种情况,如果所有属性分裂的信息增益为0,那么终止?
以下面示例来说明:
| a | b | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- 如果考虑这第三种情况, 在第一步时信息增益就为0,无法选择任何属性进行分裂
- 如果不考虑这第三种情况,就可以按下图进行分裂
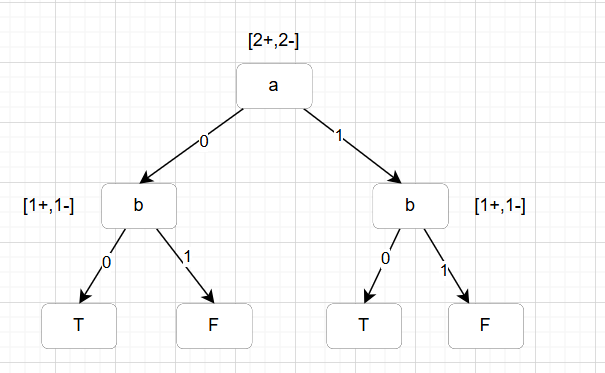
因此,只会有两种情形会停止分裂:相同的输出类别或相同的输入特征
ID3算法的特性分析
假设空间特性:
- 完备性: 目标函数必定存在于假设空间中
- 单一假设输出:通常问题规模不超过20个属性
- 无回溯贪心搜索:可能陷入局部最优解
- 全数据利用:对噪声数据具有一定的鲁棒性
归纳偏置
- 假设空间:不对假设空间施加限制
- 搜索偏置:偏好信息增益大的属性靠近根节点
- 奥卡姆剃刀原则:偏向于最简单的合理解释
- 实现方法:通过信息增益最大化来实现简洁性偏好
CART (分类和回归树)
一个通用的框架:
- 根据训练数据构建一棵决策树
- 决策树会逐渐把训练集合分成越来越小的子集
- 当子集纯净后不再分裂
- 或者接受一个不完美的决策
许多决策树算法都在这个框架下,包括ID3、C4.5等等。
下篇预告
在下一章中,我们将深入探讨决策树学习中的过拟合问题、剪枝技术、连续属性处理方法以及决策树在实际应用中的扩展和优化策略。