数据结构_哈夫曼编码（Huffman）完整指南：从原理到实现，附考研真题详解

jinmo_C++2025-10-10 14:14

目录

哈夫曼编码的基本概念

哈夫曼编码是一种经典的无损数据压缩算法，由David A. Huffman于1952年提出。它通过构建最优二叉树来实现字符的高效编码，频率高的字符使用短编码，频率低的字符使用长编码，从而达到压缩数据的目的。本文将深入分析一个完整的哈夫曼树实现，探讨其设计理念和实现细节。

为什么哈夫曼编码是最优变长编码？

在传统的数据传输中采用ASCII码表定长编码，一个字符的传输固定占用8个bit，这样做会导致大量的空间被占用，由此衍生出了可变长编码-哈夫曼编码，哈夫曼编码根据频率构建出树形结构，使得频率最低的字符出现在距离根节点最远的地方，同时编码最长，频率高的字符出现在距离根节点最近的地方，同时编码最短。

1.1 传统定长编码的局限性

  • 在传统的数据传输中，ASCII码表采用定长编码，每个字符固定占用8个bit。这种编码方式简单直观，但存在明显的效率问题：

  • 空间浪费：对于文本中频繁出现的字符（如英文中的'e','a','t'等）与罕见字符（如'z','q','x'等）使用相同长度的编码

  • 统计特性利用不足：未能利用自然语言中字符出现频率的统计规律性

1.2 变长编码的基本思想

变长编码基于信息论的基本原理：出现概率高的事件应该赋予较短的编码，出现概率低的事件可以赋予较长的编码。这种思想最早可以追溯到香农的信息论，但哈夫曼提供了构造最优前缀码的具体方法。

2.1 前缀码特性

  • 哈夫曼编码是一种前缀码（Prefix Code），即任何一个字符的编码都不是另一个字符编码的前缀。这个特性确保了编码的唯一可解码性，无需分隔符就能正确解析。

3.1贪心选择性质

哈夫曼算法采用贪心策略，每次选择频率最低的两个节点合并。这种局部最优选择能够保证全局最优，因为：

合并后的新节点可以看作一个"超级字符"，其频率为两个子节点频率之和

原问题的最优解包含这个合并操作的最优解

构建哈夫曼树算法核心逻辑

本篇文章采用的规则为左小右大规则，左0右1规则

1.结构定义

c 复制代码 
typedef struct Node {
	char val;
	int freq;
	struct Node* lchild, * rchild;
}Node;

val 记录字符，freq记录字符频率，分别存储左右孩子地址。

2.构建哈夫曼树

字符以及频率，我们存储在一个结构体Node中，node_arr是存储多个这样结构体的数组

c 复制代码 
//建立哈夫曼树
Node* buildHuffmanTree(Node** node_arr, int n) {
	for (int i = 1; i < n; i++) {
		int ind1 = find_min(node_arr, n - i);
		swap(node_arr, ind1, n - i);
		int ind2 = find_min(node_arr, n - i - 1);
		swap(node_arr, ind2, n - i - 1);

		Node* node = getNewNode('\0', node_arr[n - i]->freq + node_arr[n - i - 1]->freq);
		node->lchild = node_arr[n - i];
		node->rchild = node_arr[n - i - 1];
		node_arr[n - i - 1] = node;
	}
	return node_arr[0];
}

算法思维：

根据 find_min函数，我们分别得到第一小和第二小的元素，先将其放置在数组的最后一位，和倒数第二位（方便合并），然后将其频率合并，得到一个超级字符，频率为两个元素的频率总和，左子树指向频率较小的节点，右子树指向频率较大的节点

通过一些列的合并，最终node_arr[0]，就为整个哈夫曼树的根节点，话不多说，上图

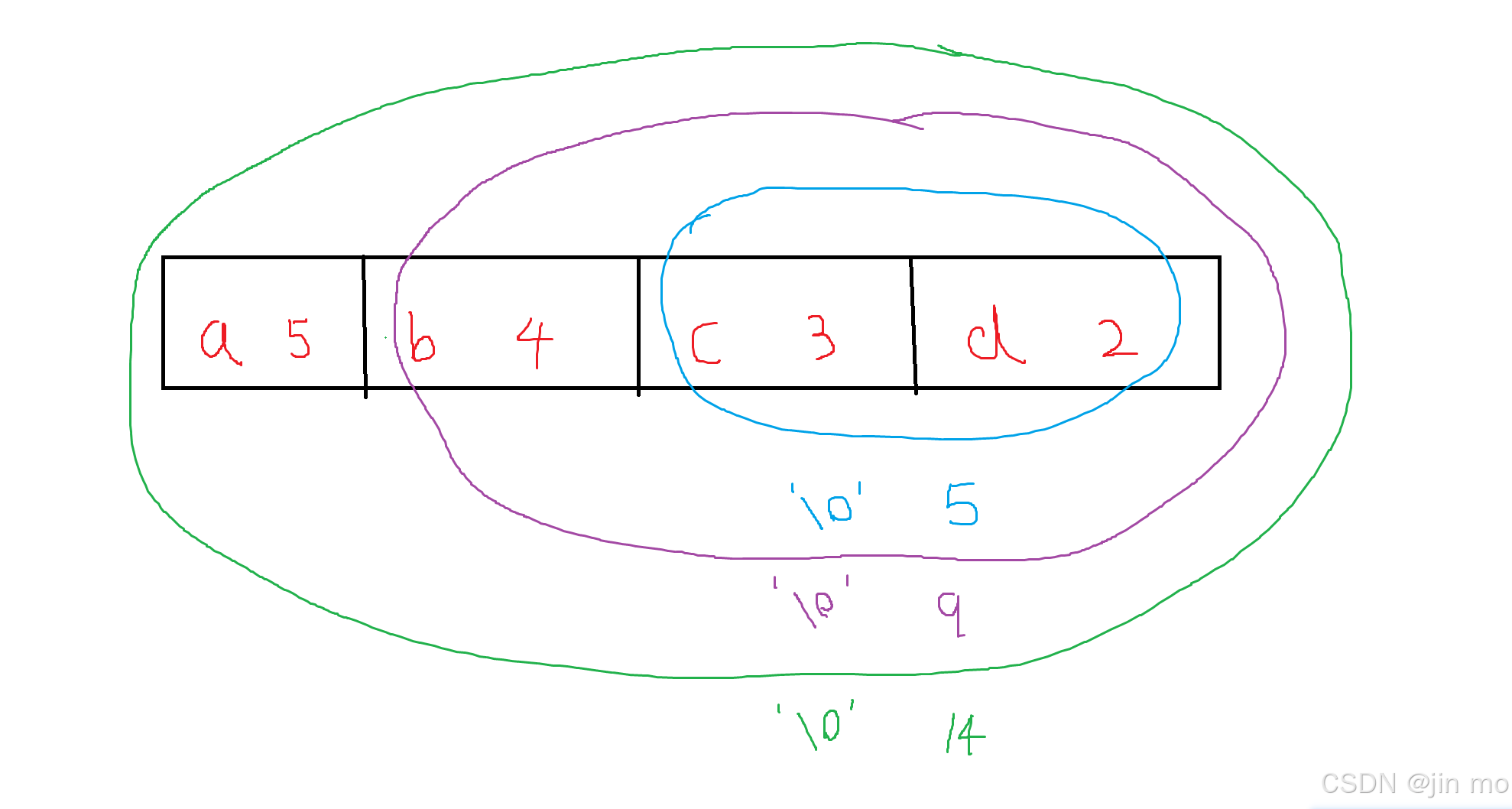
由此我们就可以构建完成整个哈夫曼树

3.获取哈夫曼编码

使用buff数组来记录路线，左0右1,char_node记录了每一个字符的编码

c 复制代码 
void extractHuffman(Node* root,char buff[],int k) {
	if (root->lchild == NULL && root->rchild == NULL) {
		buff[k] = '\0';  // ← 在这里添加结束符
		char_node[root->val] = _strdup(buff);
		return;
	}

	buff[k] = '0';
	extractHuffman(root->lchild, buff, k + 1);

	buff[k] = '1';
	extractHuffman(root->rchild, buff, k + 1);
	return;
}

算法思维：

采用递归遍历树的方式获取编码，由于哈夫曼树所求字符一定没有左右孩子（叶子节点），我们根据这一性质建立边界条件，当目前节点没有左右孩子时那么就代表找到了一个字符，将其编码存入char_node，设计完边界条件，进入函数，先进入左子树中寻找，进入前将本次路线记录为0，开始递归遍历。然后进入右子树，方法同上

核心代码逻辑就是这两个函数，下来给大家附上完整代码（可以计算WPL及其加权平均长度）：

完整代码

c 复制代码 
#define _CRT_SECURE_NO_WARNINGS
//哈夫曼编码
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<string.h>
typedef struct Node {
	char val;
	int freq;
	struct Node* lchild, * rchild;
}Node;
Node* getNewNode(char ch, int freq) {
	Node* node = (Node*)malloc(sizeof(Node));
	assert(node != NULL);//如果node为NULL则不予通过
	node->freq = freq;
	node->val = ch;
	node->lchild = node->rchild = NULL;
	return node;
}

//建立哈夫曼树
Node** node_arr;
//寻找范围中的最小值
int find_min(Node** node_arr, int n) {
	int ind = 0;
	for (int i = 0; i <= n; i++) {
		if (node_arr[i]->freq < node_arr[ind]->freq) ind = i;
	}
	return ind;
}
//交换node_arr中的元素
void swap(Node** node_arr, int pos1, int pos2) {
	Node* temp = node_arr[pos1];
	node_arr[pos1] = node_arr[pos2];
	node_arr[pos2] = temp;
	return;
}
//建立哈夫曼树
Node* buildHuffmanTree(Node** node_arr, int n) {
	for (int i = 1; i < n; i++) {
		int ind1 = find_min(node_arr, n - i);
		swap(node_arr, ind1, n - i);
		int ind2 = find_min(node_arr, n - i - 1);
		swap(node_arr, ind2, n - i - 1);

		Node* node = getNewNode('\0', node_arr[n - i]->freq + node_arr[n - i - 1]->freq);
		node->lchild = node_arr[n - i];
		node->rchild = node_arr[n - i - 1];
		node_arr[n - i - 1] = node;
	}
	return node_arr[0];
}
char *char_node[128] = { 0 };
//获取编码
void extractHuffman(Node* root,char buff[],int k) {
	if (root->lchild == NULL && root->rchild == NULL) {
		buff[k] = '\0';  // ← 在这里添加结束符
		char_node[root->val] = _strdup(buff);
		return;
	}

	buff[k] = '0';
	extractHuffman(root->lchild, buff, k + 1);

	buff[k] = '1';
	extractHuffman(root->rchild, buff, k + 1);
	return;
}
//销毁树
void clear(Node* root) {
	if (root == NULL) {
		return;
	}
	clear(root->lchild);
	clear(root->rchild);
	free(root);
}
int main()
{
	int n; scanf("%d", &n);
	node_arr=(Node **)malloc(sizeof(Node*) * n);
	char s[10];
	int freq = 0;
	int freqs[10] = {0};
	int total_freq = 0;
	for (int i = 0; i < n; i++) {
		scanf("%s %d", &s, &freq);
		total_freq += freq;
		node_arr[i] = getNewNode(s[0], freq);
		freqs[i] = freq;
	}
	char buff[1000];
	Node * root=buildHuffmanTree(node_arr, n);
	extractHuffman(root, buff,0);
	int WPL = 0;
	int index = 0;
	for (int i = 0; i < 128; i++) {
		int len = 0;
		if (char_node[i] != NULL) {
			while (char_node[i][len] != '\0') {
				len++;
			}
			printf("频率:%d 长度:%d\n", freqs[index], len);
			WPL += freqs[index++] * len;
			printf("%c %s\n", i, char_node[i]);
		}
	}
	printf("WPL:%d \n", WPL);
	printf("加权平均长度为:%.2lf", WPL*1.0 / total_freq);
	return 0;
}

核心算法复杂度分析

遍历node_arrO(N-1),寻找最小值O(N),所以构建哈夫曼树的时间复杂度为O(N2);

  • 外层循环：n-1次

  • 每次循环中调用两次 find_min()：每次O(n)

  • 总时间复杂度：O(n × n) = O(n²)

  • 虽然当前实现为O(n²)，但使用最小堆可以优化到O(n log n)"

2023年408统考数据结构选择题第四题

在由 6 个字符组成的字符集 S 中,各字符出现的频次分别为 3,4,5,6,8,10,为 S 构造的哈夫曼编码的加权平均长度为（ ）。

选项：A. 2.4 B. 2.5 C. 2.67 D. 2.75

直接用程序算，然后再手算，测试结果

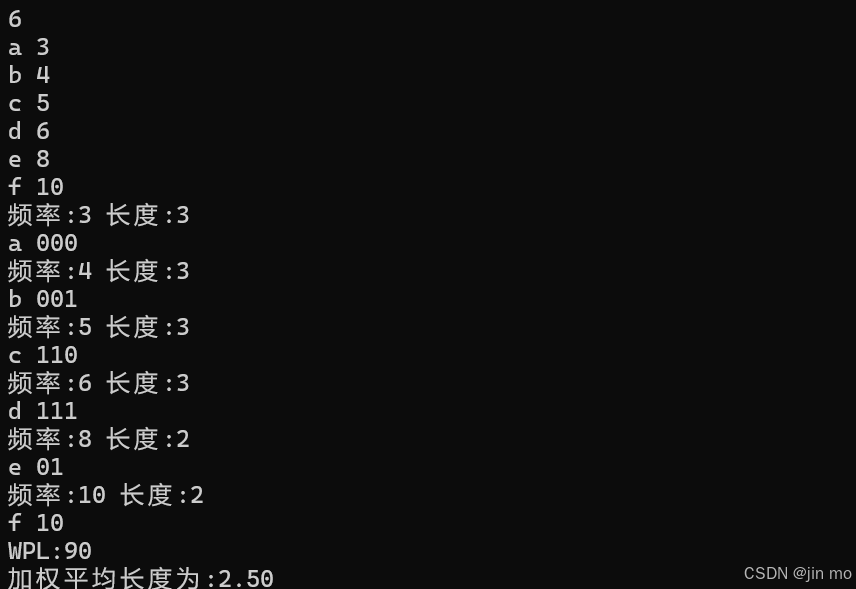
由代码算出结果为2.5选B ，下来手动模拟：

初始: [3,4,5,6,8,10]

第1步: 合并3,4 → [5,6,7,8,10] (7=3+4)

第2步: 合并5,6 → [7,8,10,11] (11=5+6)

第3步: 合并7,8 → [10,11,15] (15=7+8)

第4步: 合并10,11 → [15,21] (21=10+11)

第5步: 合并15,21 → [36]

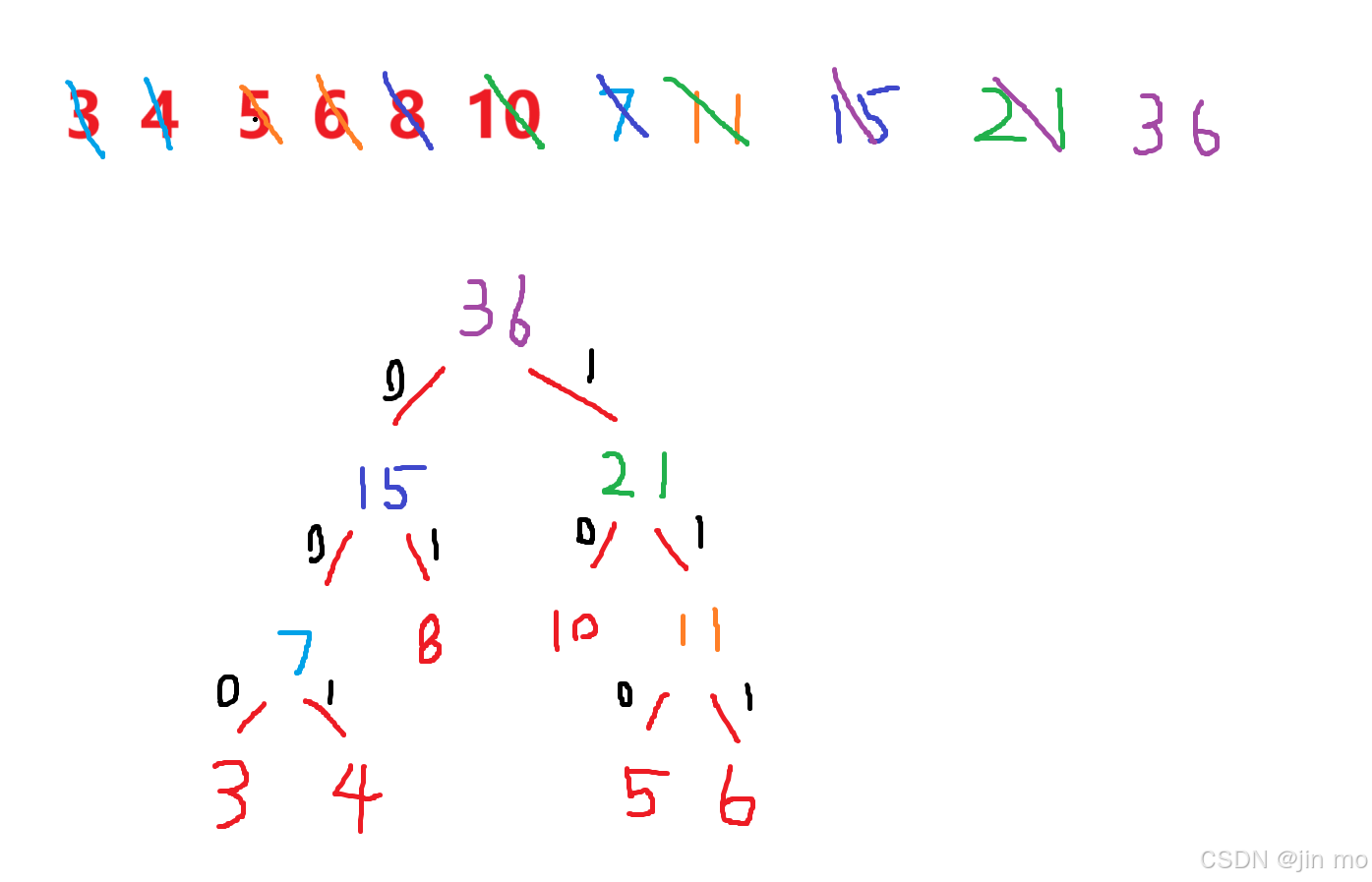
哈夫曼编码:

3:000

4:001

5:110

6:111

8:01

10:10

WPL=（3 * 3 + 4 * 3 + 5 * 3 + 6 * 3 + 8 * 2 + 10 * 2）/ 36 = (9 + 12 + 15 + 18 + 16 + 20) / 36 = 2.5

  • WPL本身是 3×3 + 4×3 + 5×3 + 6×3 + 8×2 + 10×2 = 90

  • 加权平均长度 = WPL / 总频率 = 90 / 36 = 2.5

也是2.5 得证

相关推荐
那我掉的头发算什么6 小时前
【数据结构】优先级队列（堆）
java·开发语言·数据结构·链表·idea
如竟没有火炬7 小时前
LRU缓存——双向链表+哈希表
数据结构·python·算法·leetcode·链表·缓存
爱吃生蚝的于勒7 小时前
【Linux】零基础学会Linux之权限
linux·运维·服务器·数据结构·git·算法·github
爱编程的化学家8 小时前
代码随想录算法训练营第27天 -- 动态规划1 || 509.斐波那契数列 / 70.爬楼梯 / 746.使用最小花费爬楼梯
数据结构·c++·算法·leetcode·动态规划·代码随想录
丰锋ff12 小时前
2025 年真题配套词汇单词笔记（考研真相）
笔记·考研
一只鱼^_12 小时前
力扣第470场周赛
数据结构·c++·算法·leetcode·深度优先·动态规划·启发式算法
Univin19 小时前
C++(10.4)
开发语言·数据结构·c++
Jayden_Ruan1 天前
C++十进制转二进制
数据结构·c++·算法
热门推荐
01两千字总结：Codex 国内如何安装和使用的教程，以及如何设置中文回答02UV安装并设置国内源03GitHub 镜像站点04智能库存管理的需求预测模型：从业务痛点到落地代码的完整实践0546个Nano-banana 精选提示词，持续更新中06GitLab 零基础入门指南：从安装到项目管理全流程07Linux下V2Ray安装配置指南08一文了解国产算子编程语言 TileLang，TileLang 对国产开源生态的影响与启示09jdk21下载、安装（Windows、Linux、macOS）10Cursor Plan Mode：AI 终于知道先想后做了