系列文章目录
【C++闯关笔记】map与set底层:二叉搜索树-CSDN博客
【C++闯关笔记】分析 AVL 树如此高效的原因-CSDN博客
注意,本文内容是站在前面几篇笔记的基础之上提炼总结而出的,需要对map与set,以及红黑树有一定的了解,没有相关概念的读者可点击上方链接。

文章目录
目录
前言
在之前我们介绍了map与set的底层,搜索二叉树,以及它的两种变种:AVL树与红黑树。
map与set的底层正是复用的红黑树结构。
通过分析map与set,我们可以发现它们的结构与使用逻辑十分相似,一个是K模型搜索二叉树,一个是K/V模型二叉搜索树,我们完全可以单独抽象出红黑树的逻辑代码然乎在根据实际分别实例化出Mymap与Myset。
一、map与set的底层复用:RBTree
在上篇笔记中,我们详细介绍了红黑树的概念与性质,若对红黑树不了解的读者可点击蓝字跳转:【C++闯关笔记】分析红黑树如此高效的原因-CSDN博客
下面直接给出RBTree的代码模拟实现代码。
1.树节点RBTNode
红黑树的节点通过颜色区分,所以除了正常的指针和数据成员以外,还需要设置一个colour对象保持当前节点的颜色。
如果是map,则T类型为pair<K,V>;如果是set,则T就是K类型。
cpp
namespace karsen
{
enum Colour
{
Red,
Black
};
template<class T>
struct RBTNode
{
T _date;
Colour _col;
RBTNode* _parent;
RBTNode* _left;
RBTNode* _right;
RBTNode(const T& date)
:_date(date),_col(Red)
,_parent(nullptr),_left(nullptr),_right(nullptr)
{ }
};
}2.红黑树的迭代器封装
与 list 的迭代器类似,红黑树的迭代器不能直接进行如vector的指针操作,而是需要进行的额外封装。
解释:
①T类型,即对象实例化时传入的数据类型。map传入的是pair<K,V>类型,而set则是K类型。
②Ref类型,即T&类型,决定 operator*() 的返回类型;
③Ptr类型,即T*类型,决定 operator->() 的返回类型;
④将RBTIterator<T, Ref, Ptr>,即该结构体本身typedef成 Self,方便后续使用;
⑤仅_node不是足矣,为什么要还要个_root?为了实现end()--,详见下方内容。
cpp
template<class T,class Ref,class Ptr>
struct RBTIterator
{
typedef RBTIterator<T, Ref, Ptr> Self;
typedef RBTNode<T> Node;
Node* _node;
Node* _root;
RBTIterator( Node* node = nullptr, Node* root = nullptr)
:_node(node),_root(root)
{ }
};似乎仅有一个T类型足矣,为什么还要设计class Ref,class Ptr?
------代码复用, 通过同一份代码,实例化出普通迭代器与const迭代器,避免重复编写iterator和const_iterator **。**如下所示:
cpp
class RBTree
{
public:
typedef RBTIterator<T, T&, T*> Iterator;
typedef RBTIterator<T,const T&,const T*> ConstIterator;
}关键的operator++与operator--重载
由于红黑树的遍历是中序遍历,所以operator++与operator--不能只是简单的指针+-,这也是红黑树迭代器封装主要原因之一。
operator++:
分三种情况:
情况①对于空节点,直接返回本身即可;
情况②++,即返回一个比当前节点大的一位节点。如果该节点的右子树不为空,那么右子树的最左节点就是当前节点中序遍历的下一个;(如下图中的cur(3)节点的下一个是next(4)节点,而不是6节点)
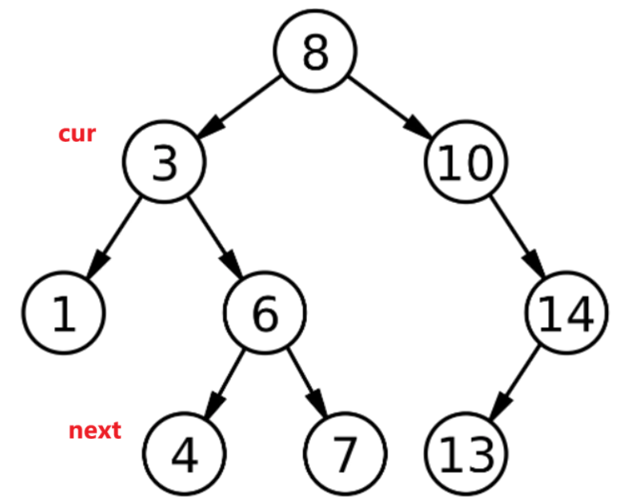
情况③如果该节点的右树为空,按中序(左 根 右)的顺序,说明该子树已经遍历完成。同样按中序(左 根 右)的顺序,下一个节点就是以该节点为左子树根节点的父节点。为什么要循环着找?------如果是最后一棵子树遍历完了,那么整棵树都遍历完了需要不断往上找根节点。
cpp
Self& operator++()
{
// 对于 end() 迭代器,++ 应该还是 end()
if (_node == nullptr)
{
return *this;
}
//右不为空,找右子树的最左节点
else if (_node->_right != nullptr)
{
Node* left = _node->_right;
while (left->_left != nullptr)
{
left = left->_left;
}
_node = left;
}
else
{
// 右为空,祖先里面孩子是父亲左的那个祖先
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_right)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}operator- -:
与++同理,依旧分三种情况,但不同的是对空(end)的处理:
情况①在红黑树中,begin函数返回的迭代器自然是整棵树最小的一个,即最左的那个。那么end函数呢?------我们默认end函数返回一个迭代器中_node值为nullptr的迭代器,即值为最大节点的下一个。那么对end返回的迭代器进行--应该就是返回值为最大的那个节点。
情况②--,返回一个比当前节点小的一位节点。如果该节点的左子树不为空,那么左子树的最右节点就是当前节点中序遍历的上一个;(如下图中的cur(3)节点的上一个是next(1)节点,而不是6节点,记得是中序(左 根 右)遍历)
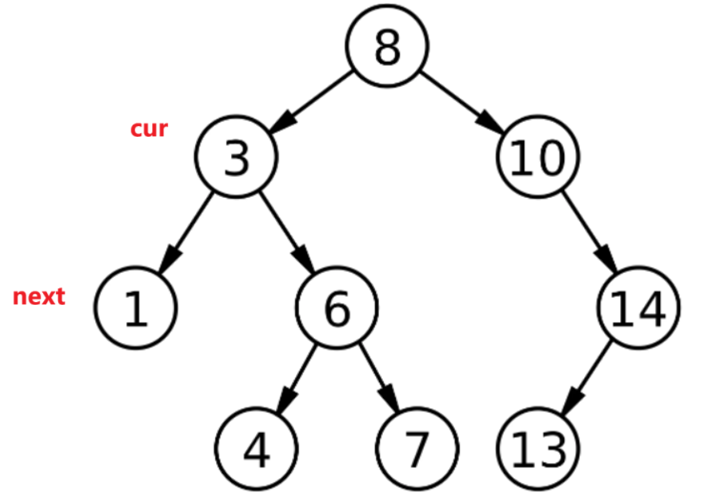
情况③如果该节点的左树为空,按中序(左 根 右)的顺序,说明该子树已经(--是倒着遍历)遍历完成。同样按中序(左 根 右)的顺序,下一个节点就是以该节点为右子树根节点的父节点。为什么要循环着找?------如果是最后一棵子树(--是倒着遍历)遍历完了,那么整棵树都遍历完了,需要不断往上找根节点。
cpp
Self& operator--()
{
//end()--应该指向最后一个元素,所以需要特殊处理
if (_node == nullptr)
{
Node* cur = _root;
while (cur->_right)
{
cur = cur->_right;
}
_node = cur;
}
//左不为空,找左子树的最右节点
else if (_node->_left != nullptr)
{
Node* right = _node->_left;
while (right->_right != nullptr)
{
right = right->_right;
}
_node = right;
}
else
{
// 左为空,祖先里面孩子是父亲右的那个祖先
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_left)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}其他操作符的重载
除去较复杂的operator++与operator--,其他操作符的重载则较为简单,这里一并给出。
值得一提的是"->":这里重载的"->"逻辑与正常使用"->"不同。正常的->类似于 (*Ptr). 类成员,而重载的->在使用过程中实际上是Ptr->->,第一个->取类成员地址,第二个->才是我们熟悉的->解引用用法,只不过是编译器在使用时将->->简化为一个->。
cpp
Ref operator*()
{
return _node->_date;
}
Ptr operator->()
{
return &(_node->_date);
}
bool operator!=(const Self& s)const
{
return _node != s._node;
}
bool operator==(const Self& s)const
{
return _node == s._node;
}3.RBTree整体结构
迭代器函数
begin函数:返回该树中序遍历的第一个节点,即概树的最左节点;
end函数:返回给树中序遍历最后一个节点的下一个位置,即nullptr。
cpp
typedef RBTIterator<T, T&, T*> Iterator;
typedef RBTIterator<T,const T&,const T*> ConstIterator;
Iterator begin()
{
Node* cur = _root;
while (cur->_left)
{
cur = cur->_left;
}
return Iterator(cur,_root);
}
ConstIterator begin()const
{
Node* cur = _root;
while (cur)
{
cur = cur->_left;
}
return make_pair(cur, _root);
}
Iterator End()
{
return Iterator(nullptr, _root);
}
ConstIterator End()const
{
return Iterator(nullptr, _root);
}后续方式释放的析构函数
cpp
public:
~RBTree()
{
Destroy(_root);
_root = nullptr;
}
private:
//采用后序遍历的方式释放节点
void Destroy(Node*root)
{
if (!root)return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
}红黑树整体代码
依据红黑树的功能,大概勾勒出红黑树类的完整结构如下。
cpp
#pragma once
#include<iostream>
#include<cassert>
namespace karsen
{
enum Colour
{
Red,
Black
};
template<class T>
struct RBTNode
{
T _date;
Colour _col;
RBTNode* _parent;
RBTNode* _left;
RBTNode* _right;
RBTNode(const T& date)
:_date(date),_col(Red)
,_parent(nullptr),_left(nullptr),_right(nullptr)
{ }
};
template<class T,class Ref,class Ptr>
struct RBTIterator
{
typedef RBTIterator<T, Ref, Ptr> Self;
typedef RBTNode<T> Node;
Node* _node;
Node* _root;
RBTIterator( Node* node = nullptr, Node* root = nullptr)
:_node(node),_root(root)
{ }
Self& operator++()
{
// 对于 end() 迭代器,++ 应该还是 end()
if (_node == nullptr)
{
return *this;
}
//右不为空,找右子树的最左节点
else if (_node->_right != nullptr)
{
Node* left = _node->_right;
while (left->_left != nullptr)
{
left = left->_left;
}
_node = left;
//错误原因:最后的left会成nullptr
//Node* left = _node->_right->_left;
//while (left)
//{
// left = left->_left;
//}
//_node = left;
}
else
{
// 右为空,祖先里面孩子是父亲左的那个祖先
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_right)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
Self& operator--()
{
//end()--应该指向最后一个元素,所以需要特殊处理
if (_node == nullptr)
{
Node* cur = _root;
while (cur->_right)
{
cur = cur->_right;
}
_node = cur;
}
//左不为空,找左子树的最右节点
else if (_node->_left != nullptr)
{
Node* right = _node->_left;
while (right->_right != nullptr)
{
right = right->_right;
}
_node = right;
}
else
{
// 左为空,祖先里面孩子是父亲右的那个祖先
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_left)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
Ref operator*()
{
return _node->_date;
}
Ptr operator->()
{
return &(_node->_date);
}
bool operator!=(const Self& s)const
{
return _node != s._node;
}
bool operator==(const Self& s)const
{
return _node == s._node;
}
};
template<class K, class T ,class KeyOfT>
class RBTree
{
typedef RBTNode<T> Node;
public:
typedef RBTIterator<T, T&, T*> Iterator;
typedef RBTIterator<T,const T&,const T*> ConstIterator;
Iterator begin()
{
Node* cur = _root;
while (cur->_left)
{
cur = cur->_left;
}
return Iterator(cur,_root);
}
ConstIterator begin()const
{
Node* cur = _root;
while (cur)
{
cur = cur->_left;
}
return make_pair(cur, _root);
}
Iterator End()
{
return Iterator(nullptr, _root);
}
ConstIterator End()const
{
return Iterator(nullptr, _root);
}
std::pair<Iterator,bool> Insert(const T& data)
{
if (!_root)
{
_root = new Node(data);
_root->_col = Black;
_count++;
return { Iterator(_root,_root), true};
}
KeyOfT kot;
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (kot(cur->_date) < kot(data))
{
parent = cur;
cur = cur->_left;
}
else if (kot(cur->_date) > kot(data))
{
parent = cur;
cur = cur->_right;
}
else
{
return { Iterator(cur,_root), false };
}
}
cur = new Node(data);
Node* NewNode = cur;
if(kot(data) < kot(parent->_date))
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent;
_count++;
//检查是否违反颜色规则
while (parent && parent->_col==Red )
{
Node* grandfather = parent->_parent;
Node* uncle = nullptr;
if (parent == grandfather->_left)
{
uncle = grandfather->_right;
if (uncle && uncle->_col == Red)
{
uncle->_col = Black;
parent->_col = Black;
grandfather->_col = Red;
cur = grandfather;
parent = cur->_parent;
}
else
{
if (cur == parent->_left)
{
RotateR(grandfather);
grandfather->_col = Red;
parent->_col = Black;
}
else
{
RotateL(parent);
RotateR(grandfather);
cur->_col = Black;
grandfather->_col = Red;
}
break;
}
}
else
{
uncle = grandfather->_left;
if (uncle && uncle->_col == Red)
{
uncle->_col = Black;
parent->_col = Black;
grandfather->_col = Red;
cur = grandfather;
parent = cur->_parent;
}
else
{
if (cur == parent->_right)
{
RotateL(grandfather);
grandfather->_col = Red;
parent->_col = Black;
}
else
{
RotateR(parent);
RotateL(grandfather);
cur->_col = Black;
grandfather->_col = Red;
}
break;
}
}
}
_root->_col = Black;
return { Iterator(NewNode,_root), true };
}
Iterator Find(const K& key)
{
Node* cur = _root;
KeyOfT kot;
while (cur)
{
if (kot(cur->_date) < key)
{
cur = cur->_right;
}
else if(kot(cur->_date) > key)
{
cur = cur->_left;
}
else
{
return Iterator(cur, _root);
}
}
return End();
}
size_t Size()
{
return _Size(_root);
}
void InOrder()
{
_InOrder(_root);
}
~RBTree()
{
Destroy(_root);
_root = nullptr;
}
private:
//采用后序遍历的方式释放节点
void Destroy(Node*root)
{
if (!root)return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
void _InOrder(Node* root)
{
if (!root)return;
_InOrder(root->_left);
std::cout << root->_date.first << ':' << root->_date.second << std::endl;
_InOrder(root->_right);
}
size_t _Size()
{
return _count;
}
void RotateR(Node* parent)
{
if (!parent || !(parent->_left))return;
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)subLR->_parent = parent;
Node* pParent = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (!pParent)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
subL->_parent = pParent;
if (pParent->_left == parent)pParent->_left = subL;
else pParent->_right = subL;
}
}
void RotateL(Node* parent)
{
if (!parent || !(parent->_right))return;
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)subRL->_parent = parent;
Node* pParent = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (!pParent)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
subR->_parent = pParent;
if (pParent->_left == parent)pParent->_left = subR;
else pParent->_right = subR;
}
}
private:
Node* _root = nullptr;
size_t _count = 0;
};
}解释:
①RBTree模板类的类型定义为三个,前两个为K/V类型(Key与value),第三个KeyOfT为仿函数,主要自实现map类中从传入的pair<K,V>数据类型中取出Key,详见下文。
②RBTree()=default;强制编译器生成默认构造函数。在这里使用默认的构造函数即可,insert会自动调用节点RBTNode的构造函数构造节点。
③Insert函数与它的子函数RotateR、RotateL十分负债,在上一篇笔记中用了大量图文解释,这里就不再赘述,可以点击蓝色字体跳转阅读:【C++闯关笔记】分析红黑树如此高效的原因-CSDN博客
④Find函数利用了红黑树(二叉搜索树)本身的特定:左子树一定比根节点值小,右子树一定比根大。通过循环逐个比较,找到则返回成迭代器类型,没有则返回End( )。
二、用红黑树封装Myset与Mymap
1.Mymap
KeyOfT
我们先介绍上面常说的KeyOfT究竟是什么:
cpp
class Mymap
{
struct MapKeyOfT
{
const K& operator()(const std::pair<K, V>& kv)
{
return kv.first;
}
};
}在红黑树中的Insert函数中我们经常需要进行比较,如if (kot(cur->_date) < kot(data));我们比较的是什么?
------我们通过key键来比较数据,然后旋转合适的位置插入。可是在RBTree中的私有成员Node*root中,即RBTNode中的数据类型只用一个T类型,当传入RBTNode的数据类型是pair<K,V>类型后,我们想要从取得_data(pair<K,V>)中的key只能通过函数帮助,而KeyOfT仿函数的作用就是告诉红黑树"如何从T中提取K"!
RBTNode类型:
template<class T >
struct RBTNode
{
T _data;
}
Mymap的大致结构
cpp
namespace karsen
{
template<class K,class V>
class Mymap
{
struct MapKeyOfT{};
private:
RBTree<K, std::pair<K, V>, MapKeyOfT> _mapRoot;
};
}map在实际使用过程中需要传入两种数据类型,一个K类,一个V类型,而它们实质充当的是key与value。
可是这里为什么会用两个K呢?------让我们回想一下红黑树的类型与它的节点的类型:
RBTNode类型:
template<class T >
struct RBTNode
{
T _date;
}
RBTree类型:
template<class K, class T ,class KeyOfT>
class RBTree
{
typedef RBTIterator<T, T&, T*> Iterator;
typedef RBTIterator<T,const T&,const T*> ConstIterator;
private:
Node* _root = nullptr;
size_t _count = 0;
};
我们可以看到,在红黑树中实际起作用的仅是template<class K, class T ,class KeyOfT>中的T类型,因为RBTree中的数据成员Node* _root,中实际使用的只用T类型!
那么问题又来了,既然只用T类型,那为什么还要预留K类型?------是的,在设计红黑树之初我们就考虑到依靠红黑树实现的map了!因为map实例化必然会传如K/V两个类型,如果红黑树只设计一个类型T,那么我们就无法实现一个通用的、可复用的红黑树模板,同时支持map和set!
比如,如果只有T,红黑树不知道键的类型是什么 ,无法提供像 Find(key) 这样的接口,因为红黑树是要复用给map与set同时使用的,如果是set还好只有key,可是map却是pair<K,V>,这会导致需要对map的Find特化,显然不如一开始就提供三个参数实用。
以下总结Mymap中传给私有成员_mapRoot三个类型的作用:
-
K (第一个参数):告诉红黑树"按什么类型来比较和查找"
-
T (第二个参数):告诉红黑树"实际存储什么类型的数据"
-
KeyOfT (第三个参数):告诉红黑树"如何从T中提取K"
综上,简单来说第一个K的作用就是给KeyOfT 服务的。为什么需要KeyOfT,因为在Insert函数中会需要对传入的T类型(pair<K,V>)取K键用于比较大小!
Mymap类
于是综上所述,Mymap类代码如下
cpp
namespace karsen
{
template<class K,class V>
class Mymap
{
struct MapKeyOfT
{
const K& operator()(const std::pair<K, V>& kv)
{
return kv.first;
}
};
//typename RBTree<K, V, KeyOfT> RBTree;
public:
typedef typename RBTree<K, std::pair<K, V>, MapKeyOfT>::Iterator iterator;
typedef typename RBTree<K, std::pair<K, V>, MapKeyOfT>::ConstIterator const_iterator;
iterator begin()
{
return _mapRoot.begin();
}
iterator end()
{
return _mapRoot.End();
}
std::pair<iterator, bool> insert(const std::pair < K,V>& kv)
{
return _mapRoot.Insert(kv);
}
V& operator[](const K& key)
{
std::pair<iterator, bool> ret = insert({ key, V() });
return ret.first->second;
}
iterator find(const K& key)
{
return _mapRoot.Find(key);
}
private:
RBTree<K, std::pair<K, V>, MapKeyOfT> _mapRoot;
};
}解释:
①默认生成的构造函数与析构函数,会自动调用自定义类型的构造函数与析构函数,所以这里可以不用写;
②在typedef iterator时需要加上typename,因为编译器不知道typedef的是数据成员函数函数成员;
③红黑树的Insert函数会返回一个pair<iterator,bool>,bool里存储的是是否插入成功,所以这里直接用insert函数代替重载[ ]的核心逻辑,至于插入的V(),这是一个默认值,若外界没有输入数据,则用此值。如果Insert返回的是false,说明该成员已存在,则返回的该成员的迭代器iterator;若返回的是true,则标明插入成功,返回新插入的数据的迭代器。
2.Myset
在有Mymap的经验后,模拟实现Myset就容易多了,毕竟set只需要一个Key。
下面直接给出Myset类:
cpp
namespace karsen
{
template<class K>
class Myset
{
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
public:
typedef typename RBTree<K,const K, SetKeyOfT>::Iterator iterator;
typedef typename RBTree<K, const K, SetKeyOfT>::ConstIterator const_iterator;
iterator Begin()
{
return _setRoot.begin();
}
iterator End()
{
return _setRoot.End();
}
std::pair<iterator, bool> Insert(const K& key)
{
return _setRoot.Insert(key);
}
iterator find(const K& key)
{
return _setRoot.Find(key);
}
private:
RBTree<K,const K, SetKeyOfT> _setRoot;
};
}整体与Mymap类似。
set类在使用时只需传入一个K类型的数据即可,但是复用的RBTree的代码有三个类型<class K, class T ,class KeyOfT>,这里我们直接将Myset中的K传给RBTree前两个类型K与T即可,什么意思呢?简单来说这里直接将Myset的K类型即当K(key)用,又当T(value)用,反正set只需要一个键,哪个都可以。这里主要是配合Mymap,因为Mymap需要用到三个类型。
那Myset什为什么会有KeyOfT,他不是直接通过传入的key进行比较吗?------这是为了与map保持一致的接口,使得红黑树能够同时服务于map和set。在set中,KeyOfT的作用就是直接返回键本身,依旧是配合Mymap。
值得注意的是set不允许修改数据,因为set的底层红黑树(搜索二叉树)正是比较各节点数据大小后建立的,如果更改数据,则可能导致整棵树都失效。
总结
本文总结了从二叉搜索树到红黑树以来的内容:用红黑树模拟实现了简单的Mymap类与Myset类。
红黑树在C++中属于比较复杂的数据结构了,笔者水平有限,若文中有错误的地方,还请在评论区中挑出,以望共同进步~
读完点赞,手留余香~