美团业务研发搜推平台部算法团队创新提出可验证过程奖励机制(VSRM),针对大模型推理中的冗余回复与过度思考问题,精准奖励有效推理步骤,显著缩减输出长度并提升推理效率。VSRM通过步骤级正确率增益评估,有效抑制无效步骤,兼容主流强化学习算法,助力高效、可靠的复杂推理任务。
1 背景
以 DeepSeek-R1 为代表的大规模推理模型,通过简单有效的强化学习后训练方法,培养了强大的推理能力,但却导致模型倾向于生成冗余的回复。这使得模型在为每个输入请求生成响应时,需要花费更多的时间以及计算资源,最终消磨用户的耐心。
针对这一缺陷,来自业务研发搜推平台部的算法团队提出可验证的过程奖励机制(VSRM),鼓励 CoT 中的"有效步骤",惩戒"无效步骤",最大限度保持性能的同时,实现高效推理。
论文下载地址 :PDF
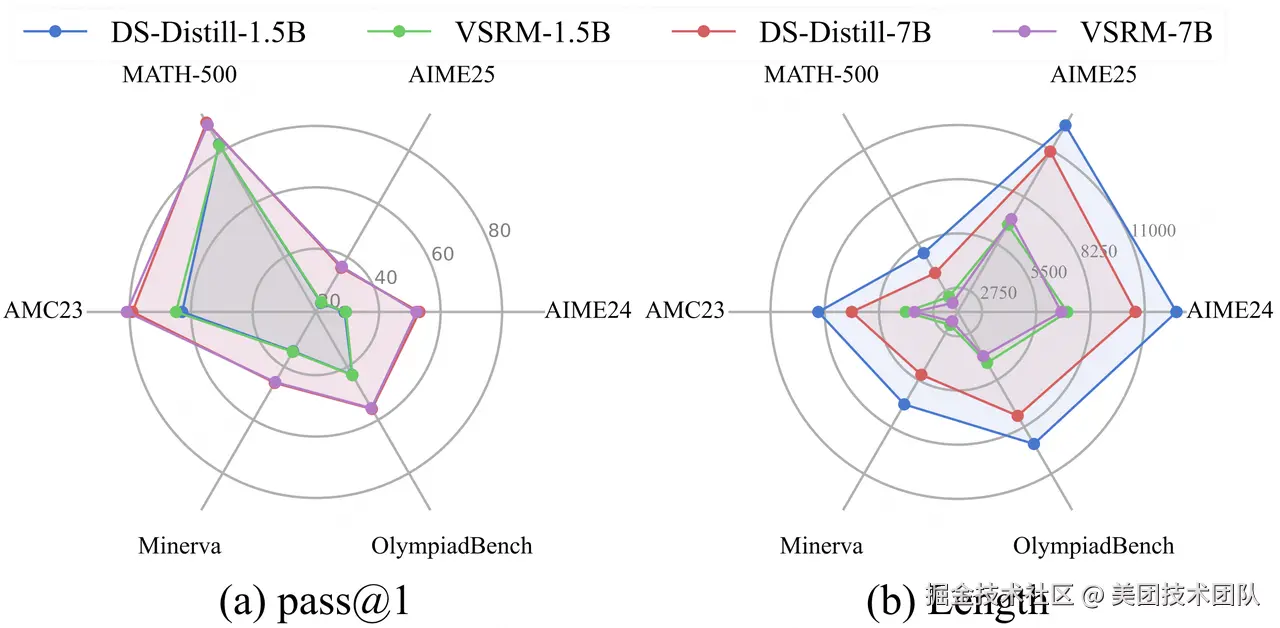
通过在数学任务上的实验显示,在多个常用 Benchmark 上,VSRM 加持的后训练使得不同尺度的模型实现了输出长度的大幅缩减,甚至在部分情况下提升了模型表现。
2 过度思考问题的本质
此前的工作将过度思考问题的现象总结为:对于一个问题,模型倾向于给出多种不同的解答,特别简单的问题。在这一认识的基础上,团队更进一步,对现有 LRM 在 MATH-500 上做出的回复进行了深入的 Case Study。

如图所示,在这个例子中,模型为解决一个非常简单的子问题([-500,0] 中有多少个小于 0 的整数)进行了反复的思考,在正确和错误之间反复横跳,最终得出了一个不正确的中间结论,进而导致了最终结论的错误。这些无效步骤不但不能指引推理路径的发展,反而会导致中间过程出错。
这样的案例并不孤立,甚至频繁出现。基于上述观察,我们团队提出:大量无效的中间步骤是导致模型过度思考的根本原因。因此,抑制这些无效步骤,鼓励有效步骤,是后训练的核心优化目标。
3 设计可验证的逐步骤奖励
现有 RLVR 的机制,通过奖励函数以可验证的二元结果奖励促进模型探索能够获得正确答案的解法。但是 结果奖励无法精确地奖惩不同的步骤,也因此无法达到所期望的目标。
过程奖励机制虽然能满足这一要求,但 过程奖励模型(PRM)往往难以训练且预测结果的可靠性有限 ,针对数学问题/代码编程等推理任务更是 严重欠缺可解释性。
搜推技术团队将可验证奖励与步骤级奖励结合在一起,创造性地提出 VSRM,为推理过程中的每个中间步骤分配奖励信号,从而实现对不同步骤的鼓励和抑制,天然地契合推理任务分步作答的特点。
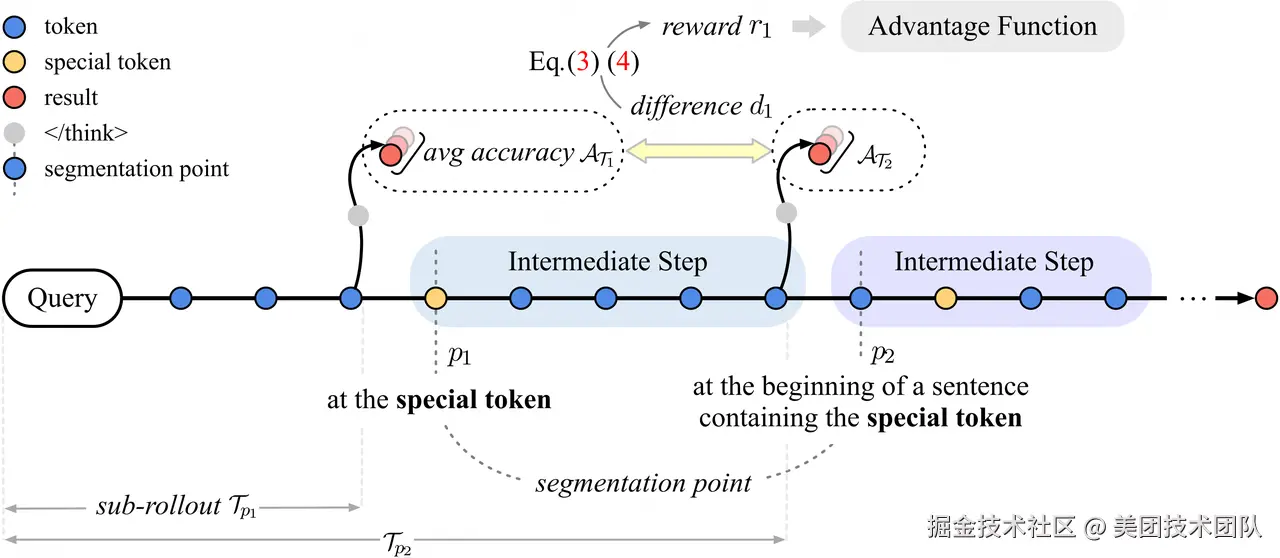
3.1 步骤划分
引入步骤级奖励的第一步是定位所有的步骤。
在 CoT 中,一些特殊的 Token,比如"However"、"Therefore"、"So"、"But"、"Wait"等往往表示模型已经完成了一个推理步骤,即将进行下一步推理(递进或是转折)。这些特殊 token 的存在将整个轨迹划分成了多个中间步骤。
为了保证划分后内容的可读性,我们额外设计了三条规则:1. 跳过最初的若干 token,这部分内容往往是对问题进行重述。2. 相邻划分点之间必须至少间隔一定距离,避免过度分割。3. 若特殊 token 位于句子内部,将划分点放在该句句首。
3.2 奖励分配
为了评估中间步骤有效与否,最直接的方式就是评估该步骤完成前后带来的正确率增益。而正确率是完全可以通过可验证的方式得到的。
只需要在每个划分点的位置前,加上一个 </think> token,这样,从 query 开始,到该处的 </think>,就构成了一条子轨迹。
以每个子轨迹为 prompt,模型能够产生多个候选答案,平均正确率体现了当前步骤得到正确答案的概率。
<math xmlns="http://www.w3.org/1998/Math/MathML"> A T i = 1 N ∑ j = i N I ( IsCorrect ( LRM ( T i ) j ) ) \mathcal{A}{\mathcal{T}{i}}=\frac{1}{N} \sum_{j=i}^{N} I\left(\operatorname{IsCorrect}\left(\operatorname{LRM}\left(\mathcal{T}{i}\right){j}\right)\right) </math>ATi=N1∑j=iNI(IsCorrect(LRM(Ti)j))
相邻子轨迹的正确率差值,即为完成当前步骤后获得的正确率增益。
<math xmlns="http://www.w3.org/1998/Math/MathML"> d i − 1 = A i − A i − 1 , for i ∈ [ 1 , ... , k ] d_{i-1}=\mathcal{A}{i}-\mathcal{A}{i-1}, \quad \text { for } i \in[1, \ldots, k] </math>di−1=Ai−Ai−1, for i∈[1,...,k]
直接将增益作为步骤级奖励就能够指导模型区分有效与无效步骤。但考虑到,往往若干个步骤才能够导致解题过程的实质性推进,因此,多个连续步骤的平均正确率很可能保持不变,进而导致稀疏的奖励信号,不利于优化。
<math xmlns="http://www.w3.org/1998/Math/MathML"> r i − 1 = sgn ( d i + q − 1 ) ⋅ ∣ d i + q − 1 ∣ ⋅ γ q r_{i-1}=\operatorname{sgn}\left(d_{i+q-1}\right) \cdot\left|d_{i+q-1}\right| \cdot \gamma^{q} </math>ri−1=sgn(di+q−1)⋅∣di+q−1∣⋅γq
为了避免这种情况,引入前瞻窗口机制,将未来的正确率变化通过折扣因子传播给当前步,从而确保奖励信号尽量密集。
通过这种机制,VSRM 机制实现了为每个步骤分配可验证的,步骤级奖励信号,从而鼓励模型减少无效步骤的输出。
与直接施加长度惩罚不同,VSRM 直接从源头上给予模型最清晰明了的奖励信号,引导模型更多选择对提升最终正确率有帮助的步骤,在缓解过度思考问题的同时,最大限度地保留模型性能。
<math xmlns="http://www.w3.org/1998/Math/MathML"> R T = [ ... , r 1 , ... , r t , ... , r k , ... , r T result + r T format ] R_{\mathcal{T}}=\left[\ldots, r_{1}, \ldots, r_{t}, \ldots, r_{k}, \ldots, r_{\mathcal{T}}^{\text {result }}+r_{\mathcal{T}}^{\text {format }}\right] </math>RT=[...,r1,...,rt,...,rk,...,rTresult +rTformat ]
VSRM 机制本身与 强化学习算法解耦,能够天然地适配支持过程奖励的方法,只需将逐步奖励添加到最终的 Reward Tensor 即可,搭配常用的结果二元结果奖励和格式奖励,即可无缝实现高效推理。
4 实验
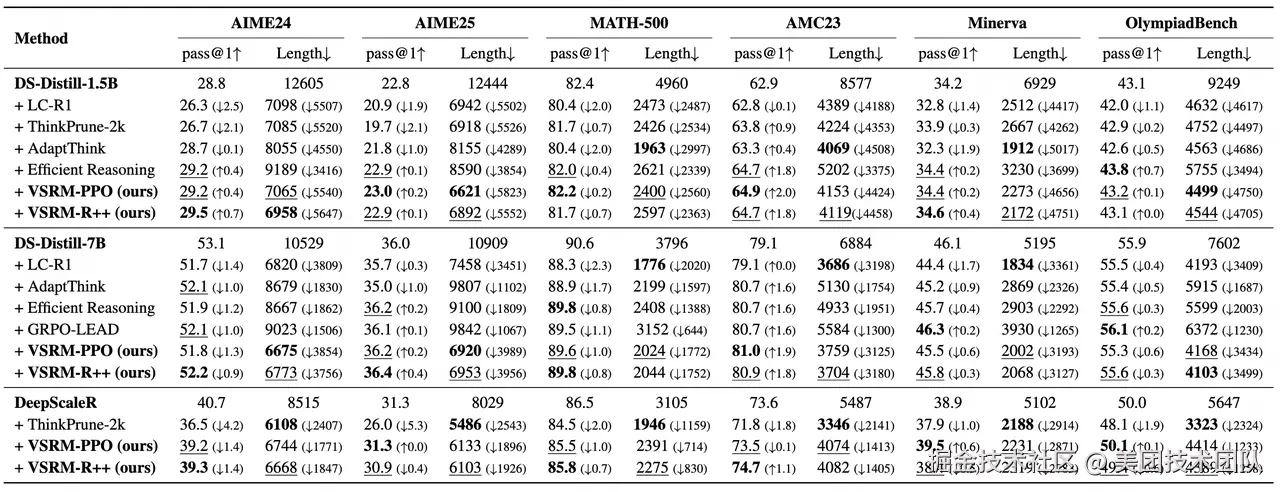
在数学问题最常用的 Benchmark 上,使用三个不同 Base Model,两种 RL 算法,将 VSRM 与多种最新的相关工作进行对比,实验结果展现出 VSRM 在降低输出长度的同时,能够最大限度地保持性能,取得很好的均衡。

消融实验的结果显示了 VSRM 中,前瞻窗口机制的有效性,以及,额外的显式长度惩罚对于 VSRM 机制并无帮助。
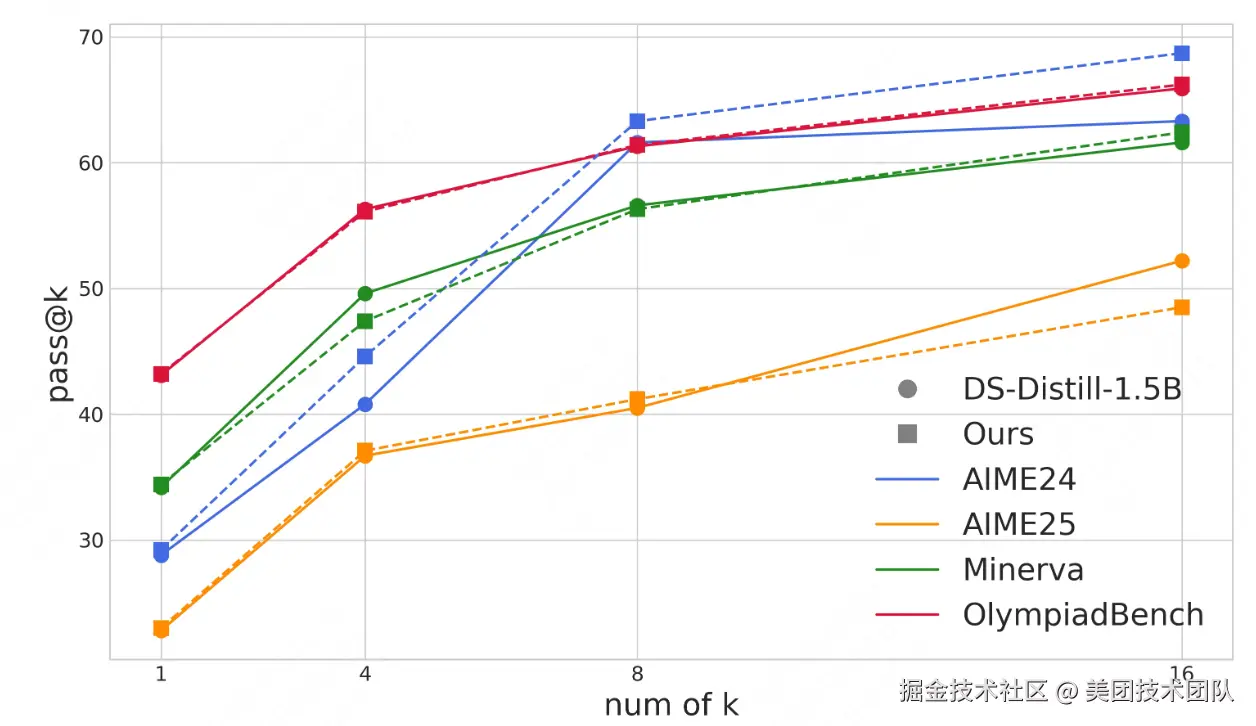
在困难 Benchmark 上,随着 k 的增加,Pass@k 指标的提升趋势能够反馈模型探索更多可行解的能力。可以看到 VSRM-PPO 训练后的模型,体现了与原本模型一致的趋势,说明模型并没有因为输出长度的压缩而失去了最重要的探索能力。
5 总结
通过广泛的对比实验,我们证明了可验证的过程奖励在不同 RL 算法,不同 Base Model 的设置下,均能实现保持性能的同时,极大缓解过度思考问题。消融实验以及进一步的实证分析也展示出,可验证的过程奖励,真正起到了抑制无效步骤,鼓励有效步骤的作用,是从根本上解决过度思考问题,保持模型良好推理行为的有效途径。
| 关注「美团技术团队」微信公众号,在公众号菜单栏对话框回复【2024年货】、【2023年货】、【2022年货】、【2021年货】、【2020年货】、【2019年货】、【2018年货】、【2017年货】等关键词,可查看美团技术团队历年技术文章合集。

| 本文系美团技术团队出品,著作权归属美团。欢迎出于分享和交流等非商业目的转载或使用本文内容,敬请注明"内容转载自美团技术团队"。本文未经许可,不得进行商业性转载或者使用。任何商用行为,请发送邮件至 tech@meituan.com 申请授权。