【C++贪心】P10537 [APIO2024] 九月|普及+

本文涉及知识点

C++贪心

[APIO2024] 九月

题目背景

请勿使用 C++14(GCC9) 提交

杭州市的中心广场有一棵著名的古树。这棵古树可以看作一棵 N N N 个节点的有根树，节点编号从 0 0 0 到 N − 1 N - 1 N−1，其中 0 0 0 号节点是根节点。

称没有孩子的节点为叶子节点。古树每次落叶时，会选择一个当前的叶子节点删去。每一天中，古树可能会多次落叶。

有 M M M 位志愿者（编号从 0 0 0 到 M − 1 M - 1 M−1）负责看护古树。每一位志愿者将各自按照如下方式独立记录今年的落叶的情况：

每一天，收集所有新的落叶的编号（即当天删除的节点的编号），然后将它们按任意顺序写在先前的落叶编号之后。

例如：第一天，叶子 3 3 3 和 4 4 4 落下，于是他们写下 3 , 4 3, 4 3,4 或 4 , 3 4, 3 4,3。第二天，叶子 1 1 1 和 2 2 2 落下，于是他们继续写下 1 , 2 1, 2 1,2 或 2 , 1 2, 1 2,1。最终的记录可能为 ( 3 , 4 , 1 , 2 ) (3, 4, 1, 2) (3,4,1,2)， ( 4 , 3 , 1 , 2 ) (4, 3, 1, 2) (4,3,1,2)， ( 3 , 4 , 2 , 1 ) (3, 4, 2, 1) (3,4,2,1) 或 ( 4 , 3 , 2 , 1 ) (4, 3, 2, 1) (4,3,2,1) 中的任意一个。

这个过程持续了 K K K 天，每天都有新的叶子掉落，直到只剩根节点为止。

你在旅途过程中经过了杭州。此刻已是寒冬，仰望古树光秃秃的枝干，你不禁想起落叶纷飞的美丽景象。

你很想知道今年有几天能看见落叶，但你只能找到 M M M 位志愿者的记录。尝试根据这些记录推断出 K K K 可能的最大值。

题目描述

你无需在程序开头引入库 september.h。

你只需要实现以下函数：

int solve(int N, int M, std::vector<int> F,
            std::vector<std::vector<int>> S);

• N N N：古树的节点数量。
• M M M：志愿者的数量。
• F F F：一个长度为 N N N 的数组。对于 1 ≤ i ≤ N − 1 1 \le i \le N - 1 1≤i≤N−1， F [ i ] F[i] F[i] 表示节点 i i i 的父亲节点的编号。 F [ 0 ] F[0] F[0] 始终为 − 1 -1 −1。
• S S S：一个长度为 M M M 的数组。 S S S 中的每个元素是一个长度为 N − 1 N - 1 N−1 的数组。 S [ i ] [ j ] S[i][j] S[i][j] 表示志愿者 i i i 记录的第 j j j 个节点编号（从 0 0 0 开始）。
• 该函数必须返回一个整数，表示根据如上规则的 K K K 可能的最大值（即，最大可能的落叶天数）。
• 对于每个测试点，交互库可能调用该函数多于一次。每次调用都应该作为新的情况分别处理。

注意：由于函数调用可能会发生多次，选手需要注意之前调用的残余数据对于后续调用的影响，尤其是全局变量的状态。

输入格式

评测程序示例读取如下格式的输入：

• 第 1 行： T T T

对于接下来 T T T 组数据中的每一组：

• 第 1 1 1 行： N M N\ M N M
• 第 2 2 2 行： F [ 1 ] F [ 2 ] ... F [ N − 1 ] F[1]\ F[2]\ \ldots\ F[N - 1] F[1] F[2] ... F[N−1]
• 第 3 + i ( 0 ≤ i ≤ M − 1 ) 3 + i\ (0 \le i \le M - 1) 3+i (0≤i≤M−1) 行： S [ i ] [ 0 ] S [ i ] [ 1 ] S [ i ] [ 2 ] ... S [ i ] [ N − 2 ] S[i][0]\ S[i][1]\ S[i][2]\ \ldots\ S[i][N - 2] S[i][0] S[i][1] S[i][2] ... S[i][N−2]

输出格式

评测程序示例按照如下格式打印你的答案：

对于每组测试数据：

• 第 1 行：函数 solve 的返回值

样例 #1

样例输入 #1

1
3 1
0 0
1 2

样例输出 #1

2

样例 #2

样例输入 #2

1
5 2
0 0 1 1 
1 2 3 4
4 1 2 3

样例输出 #2

1

提示

样例解释

对于样例一，考虑如下调用：

solve(3, 1, {-1, 0, 0}, {{1, 2}});

对应的树如下图所示：

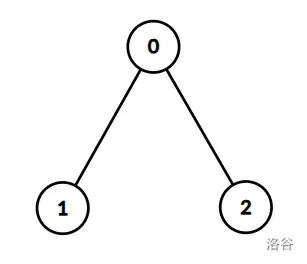
叶子 1 1 1 和 2 2 2 可能在同一天落下，或者叶子 1 1 1 在第一天先落下，然后叶子 2 2 2 在第二天落下。落叶天数不超过 2 2 2。

因此，程序应当返回 2 2 2。

对于样例二，考虑如下调用：

solve(5, 2, {-1, 0, 0, 1, 1}, {{1, 2, 3, 4}, {4, 1, 2, 3}});

对应的树如下图所示：

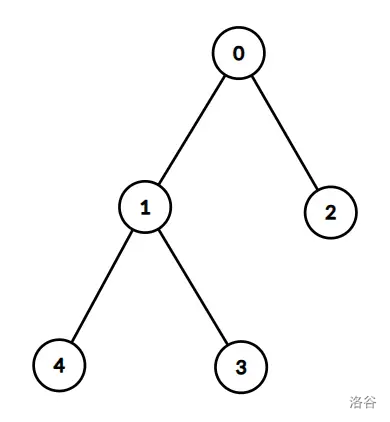
假设至少有 2 2 2 天落叶，根据志愿者的记录，叶子 4 4 4 将在不同的日子（第一天和最后一天）落下，这是矛盾的。

因此，程序应当返回 1 1 1。

数据范围

• 2 ≤ N ≤ 1 0 5 2 \le N \le 10^5 2≤N≤105
• 1 ≤ M ≤ 5 1 \le M \le 5 1≤M≤5
• ∑ N M ≤ 8 × 1 0 5 \sum NM \le 8 \times 10^5 ∑NM≤8×105
• F [ 0 ] = − 1 F[0] = -1 F[0]=−1 且对于 1 ≤ i ≤ N − 1 1 \le i \le N - 1 1≤i≤N−1, 0 ≤ F [ i ] ≤ i − 1 0 \le F[i] \le i - 1 0≤F[i]≤i−1
• 对于 1 ≤ i ≤ M − 1 1 \le i \le M - 1 1≤i≤M−1, 数组 S [ i ] S[i] S[i] 是一个 1 , 2 , ... , N − 1 1, 2, \ldots , N - 1 1,2,...,N−1 的排列
• 保证 F F F 描述的是一棵以节点 0 0 0 为根的有根树

详细子任务附加限制及分值如下表所示。

子任务编号	附加限制	分值
1	M = 1 , N ≤ 10 , ∑ N ≤ 30 M=1,N\le 10,\sum N\le 30 M=1,N≤10,∑N≤30	11 11 11
2	N ≤ 10 , ∑ N ≤ 30 N\le 10,\sum N\le 30 N≤10,∑N≤30	14 14 14
3	M = 1 , N ≤ 1   000 , ∑ N ≤ 2   000 , F [ i ] = i − 1 M=1,N\le 1\,000,\sum N\le 2\,000,F[i]=i-1 M=1,N≤1000,∑N≤2000,F[i]=i−1	5 5 5
4	M = 1 , N ≤ 1   000 , ∑ N ≤ 2   000 M=1,N\le 1\,000,\sum N\le 2\,000 M=1,N≤1000,∑N≤2000	9 9 9
5	N ≤ 1   000 , ∑ N ≤ 2   000 , F [ i ] = i − 1 N\le 1\,000,\sum N\le 2\,000,F[i]=i-1 N≤1000,∑N≤2000,F[i]=i−1	5 5 5
6	N ≤ 1   000 , ∑ N ≤ 2   000 N\le 1\,000,\sum N\le 2\,000 N≤1000,∑N≤2000	11 11 11
7	M = 1 , F [ i ] = i − 1 M=1,F[i]=i-1 M=1,F[i]=i−1	9 9 9
8	M = 1 M=1 M=1	11 11 11
9	F [ i ] = i − 1 F[i]=i-1 F[i]=i−1	9 9 9
10	没有额外的约束条件	16 16 16

贪心

依次处理各天的落叶。

令第i天，令之前已经记录j项记录。

unorder_set 将各记录员的第j项记录加到s中。j++

但 j < s.size()时 将各记录员的第j项记录加到s中。j++

如果某叶子掉了，那么它的子孙一定在当天之前掉落了。但一个叶子掉落，将没有掉落的子叶子记录到wait中。从wait中取当前叶子。

原理

假如第[0,i]天共有j片落叶，则所有记录前j项记录的落叶，排序后一定相同。

代码

核心代码

	#include <iostream>
#include <sstream>
#include <vector>
#include<map>
#include<unordered_map>
#include<set>
#include<unordered_set>
#include<string>
#include<algorithm>
#include<functional>
#include<queue>
#include <stack>
#include<iomanip>
#include<numeric>
#include <math.h>
#include <climits>

#include <bitset>
using namespace std;
	
int solve(int N, int M, std::vector<int> F,	std::vector<std::vector<int>> S) {
			vector<vector<int>> child(N);
			for (int i = 1; i  < N; i++) {	
				child[F[i]].emplace_back(i );
			}
			int ans = 0;
			unordered_set<int> s,wait;
			for (int i = 0; i+1 < N ; ) {
				ans++;
				do {
					for (const auto& v : S) {
						if (s.count(v[i])) { continue; }
						s.emplace(v[i]);
						for (const auto& c : child[v[i]]) {
							if (s.count(c)) { continue; }
							wait.emplace(c);
						}
						wait.erase(v[i]);
					}
					i++;
				}while((s.size() != i)|| wait.size());
			}
			return ans;
		}

单元测试

int N, M;
		std::vector<int> F;
		std::vector<std::vector<int>> S;
		TEST_METHOD(TestMethod11)
		{
			N = 3, M = 1, F = { -1,0,0 }, S = { { 1,2} };
			auto res = solve(N, M, F, S);
			AssertEx(2, res);
		}
		TEST_METHOD(TestMethod12)
		{
			N = 5, M = 2, F = {-1, 0, 0, 1, 1 }, S = { { 1, 2, 3, 4},{4 ,1 ,2, 3} };
			auto res = solve(N, M, F, S);
			AssertEx(1, res);
		}
		TEST_METHOD(TestMethod13)
		{
			N = 3, M = 1, F = { -1,0,1 }, S = { { 1,2} };
			auto res = solve(N, M, F, S);
			AssertEx(1, res);
		}

扩展阅读

我想对大家说的话
工作中遇到的问题，可以按类别查阅鄙人的算法文章，请点击《算法与数据汇总》。
学习算法：按章节学习《喜缺全书算法册》，大量的题目和测试用例，打包下载。重视操作
有效学习：明确的目标 及时的反馈 拉伸区（难度合适） 专注
闻缺陷则喜(喜缺)是一个美好的愿望，早发现问题，早修改问题，给老板节约钱。
子墨子言之：事无终始，无务多业。也就是我们常说的专业的人做专业的事。
如果程序是一条龙，那算法就是他的是睛
失败+反思=成功 成功+反思=成功

视频课程

先学简单的课程，请移步CSDN学院，听白银讲师（也就是鄙人）的讲解。
https://edu.csdn.net/course/detail/38771

如何你想快速形成战斗了，为老板分忧，请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176

测试环境

操作系统：win7 开发环境： VS2019 C++17

或者 操作系统：win10 开发环境： VS2022 C++17

如无特殊说明，本算法用**C++**实现。