从赌场到AI：期望值如何用C++改变世界？

我们可以把它理解为一个理论上的长期平均结果。它是衡量一个随机变量取值的"中心"或"平均值"的最重要指标。

1. 核心思想：长期的平均值

想象你反复无数次地重复同一个随机实验，期望值就是你最终会得到的平均结果。

一个简单的例子：掷骰子

一个标准的六面骰子，每个面朝上的概率是 1/6。

它的期望值计算如下：

(1 × 1/6) + (2 × 1/6) + (3 × 1/6) + (4 × 1/6) + (5 × 1/6) + (6 × 1/6) = 3.5

这意味着，如果你掷成千上万次骰子，然后把所有结果加起来求平均，这个平均值会非常接近 3.5。

注意：3.5 这个值本身是永远不可能在一次掷骰中出现的，它代表的是长期的平均水平。

2. 数学定义

期望值通常用 E(X) 或 μ 表示。

A. 离散型随机变量

如果随机变量 X 的取值是有限个或可列个，其期望定义为：
E(X) = Σ [xᵢ * P(X=xᵢ)]

即，每个可能的取值乘以它发生的概率，然后将所有这样的乘积相加。

举例：抽奖活动

你参加一个抽奖，规则如下：

中头奖（概率 1%），奖金 1000元。
中安慰奖（概率 10%），奖金 100元。
不中奖（概率 89%），奖金 0元。

这个抽奖的期望奖金是：

E(奖金) = (1000 × 0.01) + (100 × 0.1) + (0 × 0.89) = 10 + 10 + 0 = 20元

这意味着，从长远来看，你平均每次抽奖能"期望"获得20元。如果抽奖一次需要支付25元，那么长期玩下去你会亏钱。

B. 连续型随机变量

如果随机变量 X 的概率分布由概率密度函数 f(x) 描述，其期望定义为：
E(X) = ∫ [x * f(x)] dx (积分遍布 X 的所有可能取值区间)

这可以看作是离散情况的连续版本，求和变成了积分。

举例：均匀分布------"等概率" 取值的平均

1. 分布背景

均匀分布描述 "随机变量在某一区间([a, b])内等概率取值" 的情况，常见场景：

公交车站等车时间（假设公交车每 10 分钟一班，等车时间 X ~ U [0,10] )；
随机抽取一根 1 米长的绳子，剪断位置到端点的距离（X ~ U[0,1]）。

2. 概率密度函数

若X ~ U [a, b]（表示X 服从([a,b])上的均匀分布），则其概率密度函数为：
当a≤x≤b,(f(x)=1/(b−a)) 当 a≤x≤b ,( f(x) = 1/(b-a) ) 当a≤x≤b,(f(x)=1/(b−a))

当x<a或x>b,(f(x)=0) 当x<a或x>b,( f(x) = 0 ) 当x<a或x>b,(f(x)=0)

含义：区间([a,b])内，概率密度处处相等（体现"等概率"）；区间外密度为0（不可能取值）。

3. 期望计算

根据连续型期望公式，代入(f(x))计算（积分区间仅需考虑([a,b])，区间外(f(x)=0)，积分贡献为0）：

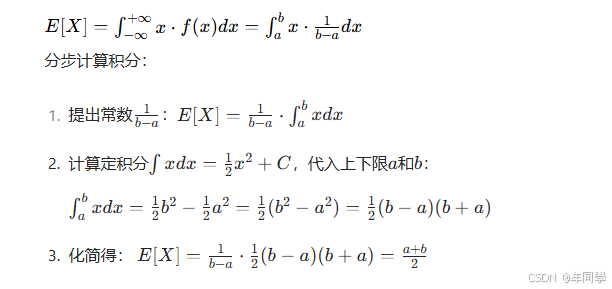
4. 实际意义

均匀分布的期望是区间([a,b])中点，完全符合直觉------"等概率取值时，平均值就是区间中间位置"。

例如：

公交车每10分钟一班，等车时间 X~U[0,10]，期望(E[X] =(0+10)/2 = 5分钟（平均等5分钟）；
绳子剪断位置X~U[0,1]，期望(E[X] = 0.5)米（平均剪断在中间位置）。

3. 期望的性质（非常有用！）

期望之所以强大，是因为它有一些非常好的数学性质，无论随机变量是否独立，这些性质都成立：

线性性质：这是最重要的性质。
- E(aX + b) = aE(X) + b (其中 a, b 是常数)
- E(X + Y) = E(X) + E(Y) (对任意两个随机变量 X, Y 都成立)
- 更一般地：E(aX + bY + c) = aE(X) + bE(Y) + c
独立变量的乘积 ：如果两个随机变量 X 和 Y 相互独立，那么：
- E(XY) = E(X) * E(Y)

4. 理解期望时需要注意的要点

期望值不等于"必然"值：就像掷骰子的期望是3.5，但你永远掷不出3.5。它描述的是整体趋势，而非单次结果。
期望可能没有意义：在某些分布（如柯西分布）中，期望值是不存在的（积分不收敛）。
期望不能完全描述分布 ：两个完全不同的分布可以有相同的期望值。
- 例如，一个投资有50%概率赚100万，50%概率亏100万，期望收益是0。
- 另一个投资是100%概率不赚不亏，期望收益也是0。
- 虽然期望相同，但风险（方差）天差地别。因此，在评估风险时，我们还需要"方差"这个概念。

5、程序完整示例（c++）

下面是用C++实现概率论中期望的示例，包括离散和连续两种情况：

cpp 复制代码

#include <iostream>
#include <vector>
#include <functional>
#include <cmath>
#include <iomanip>

// 离散型随机变量的期望计算
class DiscreteExpectation {
public:
    // 计算离散随机变量的期望
    static double calculate(const std::vector<double>& values, 
                          const std::vector<double>& probabilities) {
        if (values.size() != probabilities.size()) {
            throw std::invalid_argument("Values and probabilities must have same size");
        }
        
        double expectation = 0.0;
        double prob_sum = 0.0;
        
        for (size_t i = 0; i < values.size(); ++i) {
            expectation += values[i] * probabilities[i];
            prob_sum += probabilities[i];
        }
        
        // 验证概率和是否为1（允许小的浮点误差）
        if (std::abs(prob_sum - 1.0) > 1e-6) {
            std::cout << "Warning: Probabilities sum to " << prob_sum << ", expected 1.0" << std::endl;
        }
        
        return expectation;
    }
};

// 连续型随机变量的期望计算
class ContinuousExpectation {
public:
    // 使用数值积分计算连续随机变量的期望
    // f: 概率密度函数
    // a, b: 积分区间
    // n: 分割数
    static double calculate(std::function<double(double)> pdf, 
                           double a, double b, int n = 1000) {
        if (a >= b) {
            throw std::invalid_argument("a must be less than b");
        }
        
        double h = (b - a) / n;  // 步长
        double expectation = 0.0;
        
        // 使用梯形法则进行数值积分
        for (int i = 0; i <= n; ++i) {
            double x = a + i * h;
            double weight = (i == 0 || i == n) ? 0.5 : 1.0;  // 梯形法则权重
            expectation += weight * x * pdf(x);
        }
        
        expectation *= h;
        return expectation;
    }
};

// 示例函数
void runExamples() {
    std::cout << std::fixed << std::setprecision(4);
    
    // ==================== 离散型期望示例 ====================
    std::cout << "=== 离散型随机变量期望示例 ===" << std::endl;
    
    // 示例1: 掷骰子
    {
        std::vector<double> dice_values = {1, 2, 3, 4, 5, 6};
        std::vector<double> dice_probs = {1.0/6, 1.0/6, 1.0/6, 1.0/6, 1.0/6, 1.0/6};
        double dice_expectation = DiscreteExpectation::calculate(dice_values, dice_probs);
        std::cout << "1. 掷骰子期望: " << dice_expectation << std::endl;
        std::cout << "   (理论值: 3.5000)" << std::endl << std::endl;
    }
    
    // 示例2: 抽奖活动
    {
        std::vector<double> lottery_values = {1000, 100, 0};  // 奖金
        std::vector<double> lottery_probs = {0.01, 0.10, 0.89}; // 概率
        double lottery_expectation = DiscreteExpectation::calculate(lottery_values, lottery_probs);
        std::cout << "2. 抽奖活动期望奖金: " << lottery_expectation << "元" << std::endl;
        std::cout << "   (理论值: 20.0000)" << std::endl;
        
        // 分析是否值得参与
        double ticket_price = 25.0;
        std::cout << "   门票价格: " << ticket_price << "元" << std::endl;
        std::cout << "   期望收益: " << (lottery_expectation - ticket_price) << "元" << std::endl;
        std::cout << "   结论: " << ((lottery_expectation > ticket_price) ? "值得参与" : "不值得参与") 
                  << std::endl << std::endl;
    }
    
    // 示例3: 二项分布 (抛10次硬币，正面次数)
    {
        int n_trials = 10;
        double p_success = 0.5;
        
        std::vector<double> binomial_values;
        std::vector<double> binomial_probs;
        
        for (int k = 0; k <= n_trials; ++k) {
            // 二项分布概率: C(n,k) * p^k * (1-p)^(n-k)
            double prob = std::tgamma(n_trials + 1) / (std::tgamma(k + 1) * std::tgamma(n_trials - k + 1))
                         * std::pow(p_success, k) * std::pow(1 - p_success, n_trials - k);
            binomial_values.push_back(k);
            binomial_probs.push_back(prob);
        }
        
        double binomial_expectation = DiscreteExpectation::calculate(binomial_values, binomial_probs);
        std::cout << "3. 抛10次硬币正面次数的期望: " << binomial_expectation << std::endl;
        std::cout << "   (理论值: " << n_trials * p_success << ")" << std::endl << std::endl;
    }
    
    // ==================== 连续型期望示例 ====================
    std::cout << "=== 连续型随机变量期望示例 ===" << std::endl;
    
    // 示例4: 均匀分布 (公交车等待时间)
    {
        double a = 0.0, b = 60.0;  // 等待时间在0-60分钟之间均匀分布
        
        // 均匀分布的概率密度函数
        auto uniform_pdf = [a, b](double x) {
            return (x >= a && x <= b) ? 1.0 / (b - a) : 0.0;
        };
        
        double uniform_expectation = ContinuousExpectation::calculate(uniform_pdf, a, b);
        std::cout << "4. 公交车等待时间期望: " << uniform_expectation << "分钟" << std::endl;
        std::cout << "   (理论值: " << (a + b) / 2 << ")" << std::endl << std::endl;
    }
    
    // 示例5: 指数分布 (设备寿命)
    {
        double lambda = 0.1;  // 失效率
        
        // 指数分布的概率密度函数
        auto exponential_pdf = [lambda](double x) {
            return (x >= 0) ? lambda * std::exp(-lambda * x) : 0.0;
        };
        
        double exp_expectation = ContinuousExpectation::calculate(exponential_pdf, 0, 100);
        std::cout << "5. 指数分布设备寿命期望: " << exp_expectation << "小时" << std::endl;
        std::cout << "   (理论值: " << 1.0 / lambda << ")" << std::endl << std::endl;
    }
    
    // 示例6: 正态分布
    {
        double mu = 5.0, sigma = 2.0;  // 均值和标准差
        
        // 正态分布的概率密度函数
        auto normal_pdf = [mu, sigma](double x) {
            return (1.0 / (sigma * std::sqrt(2 * M_PI))) 
                   * std::exp(-0.5 * std::pow((x - mu) / sigma, 2));
        };
        
        // 在[μ-3σ, μ+3σ]区间积分，覆盖99.7%的概率
        double normal_expectation = ContinuousExpectation::calculate(normal_pdf, mu - 3*sigma, mu + 3*sigma, 2000);
        std::cout << "6. 正态分布N(" << mu << "," << sigma << ")的期望: " << normal_expectation << std::endl;
        std::cout << "   (理论值: " << mu << ")" << std::endl << std::endl;
    }
}

// 演示期望的线性性质
void demonstrateLinearity() {
    std::cout << "=== 期望的线性性质演示 ===" << std::endl;
    
    // 定义两个离散随机变量
    std::vector<double> X_values = {1, 2, 3};
    std::vector<double> X_probs = {0.2, 0.5, 0.3};
    
    std::vector<double> Y_values = {10, 20};
    std::vector<double> Y_probs = {0.6, 0.4};
    
    // 计算 E(X) 和 E(Y)
    double E_X = DiscreteExpectation::calculate(X_values, X_probs);
    double E_Y = DiscreteExpectation::calculate(Y_values, Y_probs);
    
    std::cout << "E(X) = " << E_X << std::endl;
    std::cout << "E(Y) = " << E_Y << std::endl;
    
    // 验证线性性质: E(aX + bY + c) = aE(X) + bE(Y) + c
    double a = 2.0, b = 3.0, c = 5.0;
    double linear_combination = a * E_X + b * E_Y + c;
    
    std::cout << "E(" << a << "X + " << b << "Y + " << c << ") = " 
              << a << "*E(X) + " << b << "*E(Y) + " << c << " = " 
              << linear_combination << std::endl;
    
    std::cout << "这验证了期望的线性性质: E(aX + bY + c) = aE(X) + bE(Y) + c" << std::endl;
}

int main() {
    try {
        std::cout << "概率论中期望的C++实现示例" << std::endl;
        std::cout << "=========================================" << std::endl;
        
        runExamples();
        demonstrateLinearity();
        
    } catch (const std::exception& e) {
        std::cerr << "错误: " << e.what() << std::endl;
        return 1;
    }
    
    return 0;
}

主要特性：

1. 离散型期望

掷骰子：6个面概率相等，期望3.5
抽奖活动：不同奖项对应不同概率
二项分布：抛硬币正面次数的期望

2. 连续型期望

均匀分布：公交车等待时间
指数分布：设备寿命
正态分布：使用数值积分近似计算

3. 期望性质验证

线性性质的数学验证

编译和运行：

bash 复制代码

g++ -std=c++11 -o expectation expectation.cpp -lm
./expectation

输出示例：

复制代码

=== 离散型随机变量期望示例 ===
1. 掷骰子期望: 3.5000
   (理论值: 3.5000)

2. 抽奖活动期望奖金: 20.0000元
   (理论值: 20.0000)
   门票价格: 25.0000元
   期望收益: -5.0000元
   结论: 不值得参与

=== 连续型随机变量期望示例 ===
4. 公交车等待时间期望: 30.0000分钟
   (理论值: 30.0000)

关键理解点：

离散期望 = Σ(值 × 概率)
连续期望 = ∫(x × 概率密度函数)dx
期望值是长期平均值，单次结果可能不同
线性性质让复杂计算变得简单

总结

是什么：期望是随机变量所有可能值按其发生概率加权后的"长期"平均值。
怎么算：离散型用加权求和，连续型用积分。
为什么重要：它提供了预测长期行为、进行理性决策（如投资、保险）的核心理论工具。它的线性性质使其在复杂计算中非常方便。
局限：它不提供关于风险或波动性的任何信息。