"球极平面投影",这是一个能把整个地球(球面)几乎完美地压扁成一张平面地图的魔法。
它怎么工作?
-
想象一个透明的地球仪,北极点贴着桌面。
-
在南极点放一个点光源。
-
光线会向上照射,将地球仪上的每一个点(比如城市、山脉)投影到桌面上,形成一张地图。
它的魔法效果(和缺陷):
-
圆还是圆!地球上任何圆(无论大小,比如纬线、子午线),在投影地图上仍然是一个圆(或直线,可视为无限大的圆)。这个性质让它格外优雅。
-
保角。这意味着它保持角度不变。如果你在地球上两条路以90度角相交,在地图上它们依然以90度角相交。这对航海至关重要!
-
它无法完美!南极本身会被投影到无限远的地方,永远无法到达。所以这张地图会严重扭曲南极地区(比如南极洲看起来会无比巨大),但恰恰能完美展示整个北半球。
从数学的角度,"球极平面投影"是什么?具体地说,它主要是这样一个数学函数。
设球面上一点的坐标为 (x, y, z),满足 x^2 + y^2 + z^2 = 1(单位球面)。
从北极点(0, 0, 1) 将它投影到赤道 z = 0 的平面上。
投影点 (X, Y) 的坐标由以下公式给出(可以使用相似三角形推导):
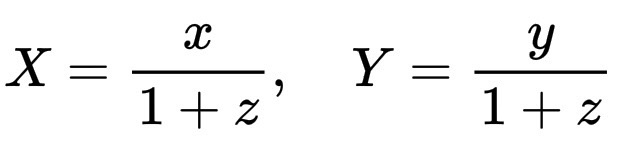
X = \frac{x}{1 + z}, \quad Y = \frac{y}{1 + z}
计算过程:
-
一个球面的数学定义(一组满足方程的点)。
-
当需要投影时,就将这个函数像调用一个子程序一样,应用到每一个点的坐标上。
-
于是,三维的 (x, y, z) 被系统地、批量地映射为二维的 (X, Y)。
【如果我想要一个"完美的地图",就把这个透明地球颠倒一下,从北极点来投影南半球。最后把南北半球拼起来就可以了?】
这个"把南北半球拼起来"的想法,已经触摸到了现代制图学的核心思想!这正是构建更精确世界地图(如各种"通用横轴墨卡托投影")的哲学,用多个不同的投影区域,拼接成一个更少失真的整体。