深度学习入门（一）——从神经元到损失函数，一步步理解前向传播（下）

七、前向传播的全景理解

前面我们讲到一个神经元的数学本质，其实整个神经网络的前向传播（Forward Propagation），就是把"加权求和 + 激活函数"这个小操作重复多次。

想象你有三层结构：

输入层（Input） → 隐藏层（Hidden） → 输出层（Output）

那么在每一层中，都要进行这样的变换：

输入向量 → 加权求和 → 激活函数输出 → 传递给下一层

伪代码如下：

# X: 输入数据
# W[i], b[i]: 第 i 层的权重和偏置
# f[i]: 第 i 层的激活函数

A[0] = X  # 第 0 层的输出就是输入数据
for i in range(1, L + 1):
    Z[i] = W[i] * A[i-1] + b[i]
    A[i] = f[i](Z[i])
return A[L]  # 最后一层的输出

这几行伪代码，实际上就是神经网络的"灵魂"：

• Z[i] 表示线性组合；

• f[i](Z[i]) 表示非线性变换；

• 最后一层输出 A[L] 就是整个网络的预测结果。

所以，神经网络不是魔法。

它只是堆叠了一堆线性变换 + 非线性激活的组合 。

而它能拟合复杂函数的原因，就是------多次"线性 + 非线性"叠加后，可以逼近任意连续函数（这就是"通用逼近定理"）。

---

八、损失函数：神经网络的"指南针"

如果说前向传播是神经网络的大脑，那么**损失函数（Loss Function）**就是它的指南针。

它决定了"模型到底学得好不好"，以及"往哪个方向去调整"。

1. 为什么需要损失函数？

想象你在教小孩写字。

你告诉他："写个'A'。"

他写完了，但你得告诉他写得好不好------不然他永远不知道哪里错了。

损失函数的作用，就是给网络一个反馈信号，告诉它预测结果和真实答案之间的差距。

---

2. 常见的损失函数类型

损失函数并不只有一种。不同任务，适合不同的定义。

(1) 均方误差（MSE）

用于回归问题：

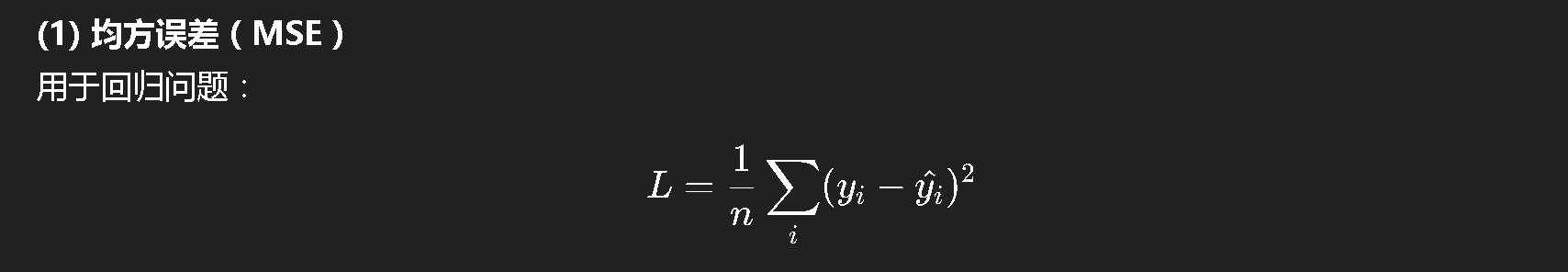
伪代码：

loss = 0
for each sample i:
    diff = (y_true[i] - y_pred[i])
    loss += diff * diff
loss = loss / n

它衡量的就是"预测值和真实值之间的平均平方距离"。

特点：

• 对误差较大的样本惩罚更重；

• 适合数值连续的任务；

• 对异常值敏感。

---

(2) 交叉熵损失（Cross Entropy）

用于分类问题，尤其是多类分类。

它刻画的是两个分布之间的"距离"。

如果 y_true 是 one-hot 向量（比如 [0, 0, 1, 0]），y_pred 是网络输出的概率分布（比如 [0.1, 0.2, 0.6, 0.1]），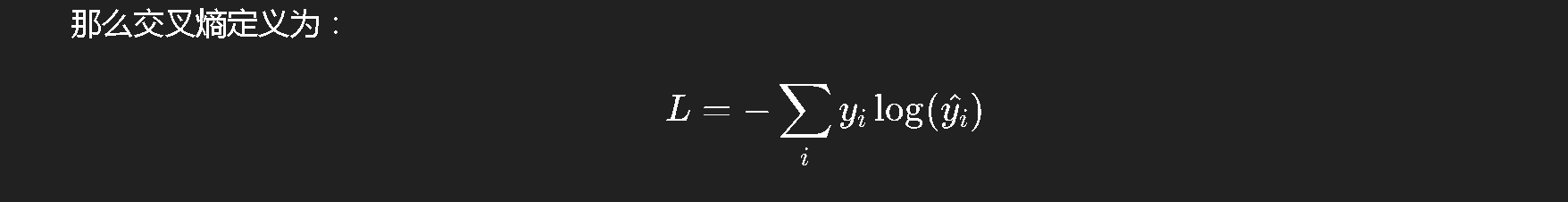

伪代码：

loss = 0
for each class i:
    loss += - y_true[i] * log(y_pred[i])

由于只有正确类别的 y_true[i] = 1，所以其实每次只取一个项。

直觉上，交叉熵衡量的是"模型把真实类别预测得有多确定"。

越确定（预测概率高），损失越低。

---

(3) Softmax + Cross Entropy 联合使用

Softmax 是一种把任意实数向量转换为概率分布的函数：

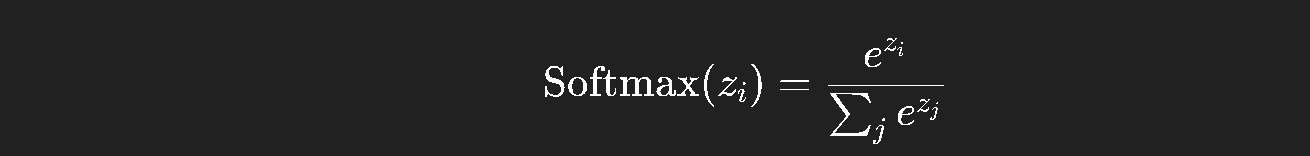
它保证所有输出在 0~1 之间，且和为 1。

但计算时要注意数值稳定性问题 ，因为 e^{z_i} 很容易溢出。

通常我们会减去最大值：

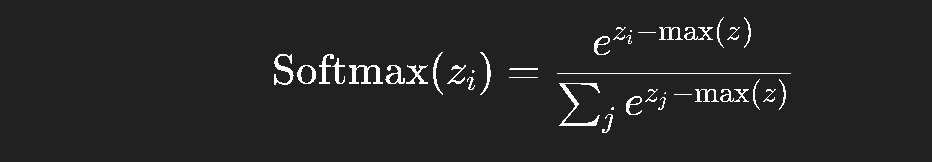
伪代码：

def stable_softmax(z):
    shift_z = z - max(z)
    exp_z = exp(shift_z)
    return exp_z / sum(exp_z)

这样就不会因为指数太大而导致 Inf 或 NaN。

---

九、从前向传播到预测：一个完整的流程

现在我们已经知道每一层的计算方式，也知道如何计算损失。

那么整个网络在一次前向传播中会经历什么？

我们来完整梳理一遍伪代码：

# 输入：训练样本 X, 标签 Y
# 参数：W[1...L], b[1...L]

# 1. 前向传播
A[0] = X
for i in range(1, L + 1):
    Z[i] = W[i] * A[i-1] + b[i]
    A[i] = f[i](Z[i])

# 2. 计算损失
loss = compute_loss(A[L], Y)

在这一步中，网络从输入数据 X 生成预测 A[L]，

然后用损失函数衡量预测和真实标签 Y 的差距。

这一套流程，被称为**"前向传播"**。

它是整个训练过程的第一阶段，也是我们下一篇要讲的"反向传播"的输入。

---

十、一个具体的例子（分类任务）

假设你想训练一个神经网络，让它区分「猫」和「狗」。

数据输入是 64x64 的灰度图片，每张展开成一个 4096 维向量。

我们构建一个简单的两层网络：

输入层 (4096) → 隐藏层 (64) → 输出层 (2)

每一层的计算逻辑如下：

# 前向传播
Z1 = W1 * X + b1
A1 = ReLU(Z1)

Z2 = W2 * A1 + b2
A2 = Softmax(Z2)

# 损失
L = -[y1 * log(A2[1]) + y2 * log(A2[2])]

其中：

• ReLU 保证特征非线性；

• Softmax 把输出映射为概率；

• L 是交叉熵损失。

你只要看懂这几行，其实已经理解了神经网络最核心的结构。

所有更复杂的模型（ResNet、Transformer）------都只是在这之上扩展而已。

---

十一、数值稳定性与浮点陷阱

在实际实现中，有几个"容易翻车"的问题：

1. 指数溢出

   • 在计算 exp(z) 时，如果 z 太大，会溢出。

   • 解决办法：使用 z - max(z) 的技巧。

2. log(0)

   • 在交叉熵中，如果 y_pred 太接近 0，log(0) 会导致 -inf。

   • 解决办法：对 y_pred 加上一个很小的 epsilon。

伪代码：

epsilon = 1e-8
loss = - sum(y_true[i] * log(y_pred[i] + epsilon))

1. 浮点误差累积

   • 多层网络在前向传播时可能积累误差。

   • 尽量使用稳定的线性代数库（如 NumPy、Torch 内置函数）。

---

十二、为什么前向传播如此重要？

有人觉得前向传播简单，但实际上，它是理解深度学习的基础。

反向传播只是"求导"前向传播的结果。

如果你连 Z = W * X + b 的含义都没有真正吃透，

那反向传播里的链式法则只是"符号游戏"。

真正理解前向传播的人，会明白：

• 每一层都在做信息的线性变换；

• 激活函数让网络具备"表达非线性"的能力；

• 损失函数提供了"方向感"。

这三者合起来，就是一个能"思考"的系统。

---

十三、总结与下一篇预告

我们在这一篇中，从最底层的神经元讲起，一步步走到了前向传播的完整结构。

你应该已经能理解以下问题：

✅ 神经元到底在计算什么？

✅ 为什么神经网络是"线性+非线性"的叠加？

✅ 损失函数在训练中扮演什么角色？

✅ Softmax 和交叉熵是怎么工作的？

✅ 实现中需要注意哪些数值细节？

如果你能把这些问题都讲清楚给别人听------

恭喜你，你已经完成了深度学习最关键的一步。