[GESP202503 五级] 原根判断

视频讲解：[GESP202503 五级] 原根判断-信息学奥赛GESP等级考试真题解析

一、原题

题目描述

小 A 知道，对于质数 p 而言，p 的原根 g 是满足以下条件的正整数：

1 < g < p；
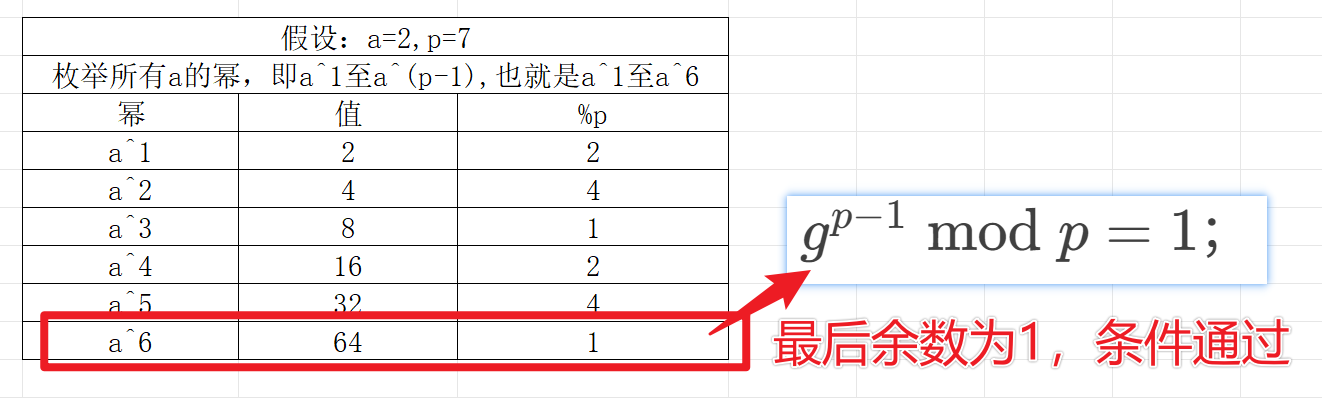
mod p =1；
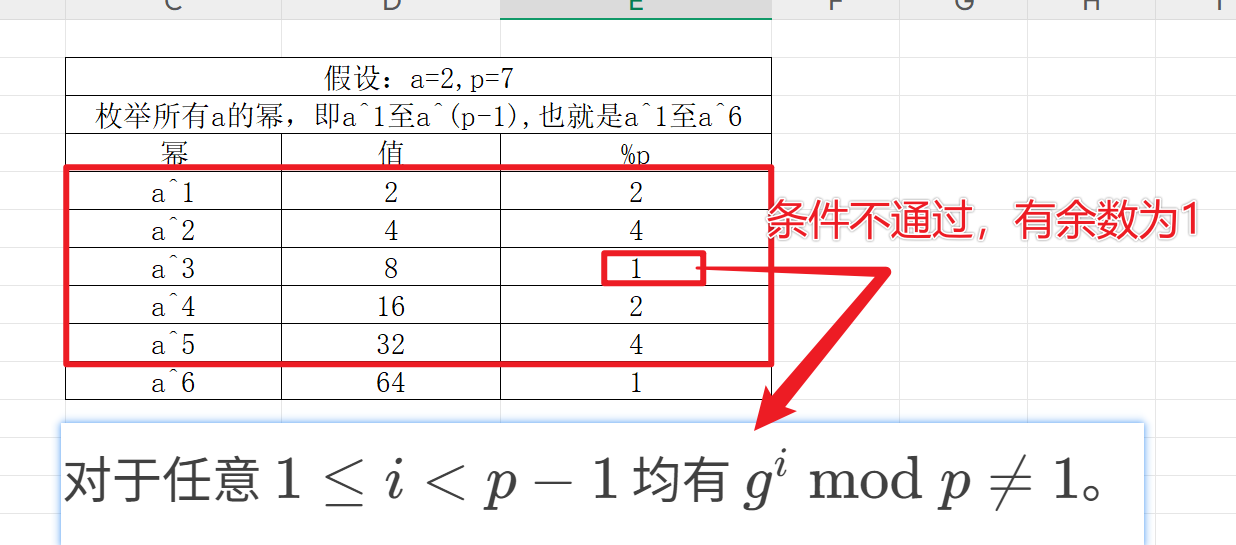
对于任意 1 ≤ i < p−1 均有 mod p≠1。

其中 a mod p 表示 a 除以 p 的余数。

小 A 现在有一个整数 a，请你帮他判断 a 是不是 p 的原根。

输入格式

第一行，一个正整数 T，表示测试数据组数。

每组测试数据包含一行，两个正整数 a,p。

输出格式

对于每组测试数据，输出一行，如果 a 是 p 的原根则输出 Yes，否则输出 No。

输入输出样例

输入 #1

cpp 复制代码

3
3 998244353
5 998244353
7 998244353

输出 #1

cpp 复制代码

Yes
Yes
No

说明/提示

数据范围

对于 40% 的测试点，保证 3 ≤ p ≤ 。

对于所有测试点，保证 1 ≤ T ≤ 20，3 ≤ p ≤ ，1<a<p，p 为质数。

二、做题思路

1)尝试暴力枚举（只能获得40分）

假设：a=2，p=7

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
int main(){
	//1)确定组数t
	int t;cin>>t;
	//2)填充t组数据
	while(t--){
		int a,p;
		cin>>a>>p;
		bool flag=true;//假设可以 
		//3)枚举所有a的幂
		//(验证条件：对于任意1<=i<p-1,均有a^i mod p!=1) 
		int now=1;
		for(int i=1;i<p-1;i++){
			now=1ll*now*a%p;
			if(now==1){
				flag=false;
				break;
			}
		}
		//4)(验证条件：a^(p-1) mod p =1)
		if(1ll*now*a%p!=1) flag=false;
		//5)根据flag输出
		cout<<(flag ? "Yes\n" : "No\n"); 
	} 
}

2)用"快速幂"解决条件：a^(p-1) mod p =1

例如a=2，p=8

cpp 复制代码

int check1(int a,int mi,int p){
	//4)快速幂求最终a^(p-1)%p的结果
	int base=a%p;
	int result=1;
	while(mi){
		if(mi&1==1){
			result=1ll*result*base%p;
		}
		base=1ll*base*base%p;
		mi=(mi>>1);
	}
	return result;
}

3)"费马小定理"解决条件：对于任意1<=i<p-1,均有a^i mod p!=1

3.1)推导过程

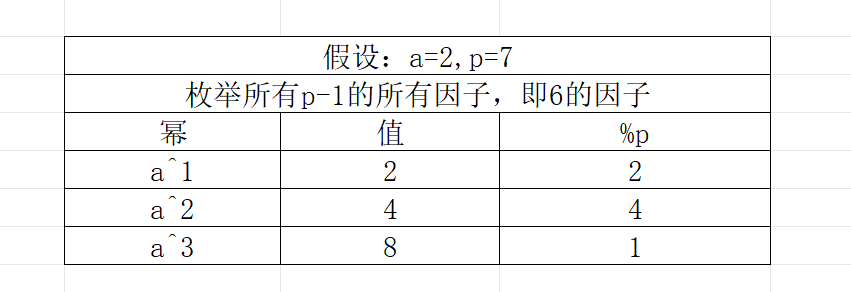
3.2) 结论：a^i mod p == 1， i必须是(p-1)的因数

cpp 复制代码

bool check2(int a,int p){
	int mi=p-1;
	//5)枚举p的所有因子
	for(int i=2;i*i<=mi;i++){
		if(mi%i==0){
			if(check1(a,i,p)==1||check1(a,mi/i,p)==1) return false;
		}
	}
	return true;
}

三、答案

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
int check1(int a,int mi,int p){
	//4)快速幂求最终a^(p-1)%p的结果
	int base=a%p;
	int result=1;
	while(mi){
		if(mi&1==1){
			result=1ll*result*base%p;
		}
		base=1ll*base*base%p;
		mi=(mi>>1);
	}
	return result;
}
bool check2(int a,int p){
	int mi=p-1;
	//5)枚举p的所有因子
	for(int i=2;i*i<=mi;i++){
		if(mi%i==0){
			if(check1(a,i,p)==1||check1(a,mi/i,p)==1) return false;
		}
	}
	return true;
}
int main(){
	//1)确定数量t
	int t;
	cin>>t;
	//2)填充t组数据
	while(t--){
		int a,p;
		cin>>a>>p;
		//3)函数判断是否可以
		if(check1(a,p-1,p)==1&&check2(a,p)) cout<<"Yes\n";
		else  cout<<"No\n";
	} 
}