文章目录
简要介绍
我们的双指针算法是算法题中比较常见的一种算法,常见的双指针实际上是有两种的,一种是对撞指针,一种就是我们的快慢指针。
对撞指针
一般用于我们的顺序结构当中,也叫左右指针。
实现思路:
1、对撞指针就是从序列两端向中间移动。
2、终止条件一般就是两个指针相遇了或是错开了。
快慢指针
这个指针又叫龟兔赛跑算法,就是使用两个移动速度不同的指针在序列上移动。常用于我们的环形链表或是数组中。
实现思路:
1、研究问题是不是有循环往复的现象出现。
2、设置一个快指针和一个慢指针,比如让快指针移动两步,慢指针移动一步。
相关例题
移动零
题目描述
给定一个数组
nums,编写一个函数将所有0移动到数组的末尾,同时保持非零元素的相对顺序。请注意 ,必须在不复制数组的情况下原地对数组进行操作。
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]示例 2:
输入: nums = [0]
输出: [0]提示:
1 <= nums.length <= 104-231 <= nums[i] <= 231 - 1
进阶:你能尽量减少完成的操作次数吗?
实现思路
版本一
这是我自己一开始想到的思路:
这个题的本质就是将我们的非零数放在数组的开头且顺序不能改变,而我们的零就要放在数组的尾端。所以可以先统计一下我们有几个非零的数,然后给一个指向开头的指针,遍历整个数组将我们的非零数一个一个的交换到我们的开头,同时我们的头指针向后移动直到我们的遍历完了非零数。
实现代码
cpp
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int cnt = 0;
for(auto& s : nums) {
if(s == 0) cnt++;
}
cnt = nums.size() - cnt;
int k = 0;
for(int i = 0; i < nums.size(); i++) {
if(nums[i] != 0) {
swap(nums[i], nums[k++]);
}
if(k > cnt) {
break;
}
}
}
};版本二
实际上上面这个代码非常的冗余,我们这里在实现的时候只需要设置一个头指针,然后将非零数直接向头位置替换即可,不需要计算什么个数。
实现代码
cpp
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int cnt = 0;
for(int i = 0; i < nums.size(); i++) {
if(nums[i]) {
swap(nums[i], nums[cnt++]);
}
}
}
};最终版
我们上面的代码实际上就是实现的双指针,只是我们遍历的下标就是我们的一个指针罢了,为了体现我们的双指针思路,我们这里给出一个比较标准的流程。
首先我们要知道我们要有两个指针,一个指针cur用来扫描我们的整个数组,一个指针dest用来记录我们的非零序列的最后一个位置,于是根据题意我们遍历的时候[0, dest]的元素都是我们的非零元素,我们的[dest - 1, cur - 1]的元素都是零元素。
1、初始化我们的cur为0,
dest = -1(指向空)。2、使用cur遍历的时候会有两种情况:
a、遍历到了0,我们继续遍历即可(满足我们的
[dest - 1, cur - 1]上面都是零元素)。b、遍历到了非零,我们就
++dest并且交换我们的cur位置和dest位置,继续遍历即可(满足[0, dest]的元素都是非零)。
实现代码
cpp
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int n=nums.size();
for(int i=0,cur=0,index=-1;i<n;i++)
{
if(nums[i])
{
swap(nums[++index],nums[i]);
}
}
}
};复写零
题目描述
给你一个长度固定的整数数组 arr ,请你将该数组中出现的每个零都复写一遍,并将其余的元素向右平移。
注意:请不要在超过该数组长度的位置写入元素。请对输入的数组 就地 进行上述修改,不要从函数返回任何东西。
示例 1:
输入:arr = [1,0,2,3,0,4,5,0]
输出:[1,0,0,2,3,0,0,4]
解释:调用函数后,输入的数组将被修改为:[1,0,0,2,3,0,0,4]示例 2:
输入:arr = [1,2,3]
输出:[1,2,3]
解释:调用函数后,输入的数组将被修改为:[1,2,3]提示:
1 <= arr.length <= 1040 <= arr[i] <= 9
实现思路
版本一
算法题还是太奇妙了,之前写的思路看了好久才看懂写了什么(bushi) ,这里是我自己一开始想到的思路,思路历程如下:
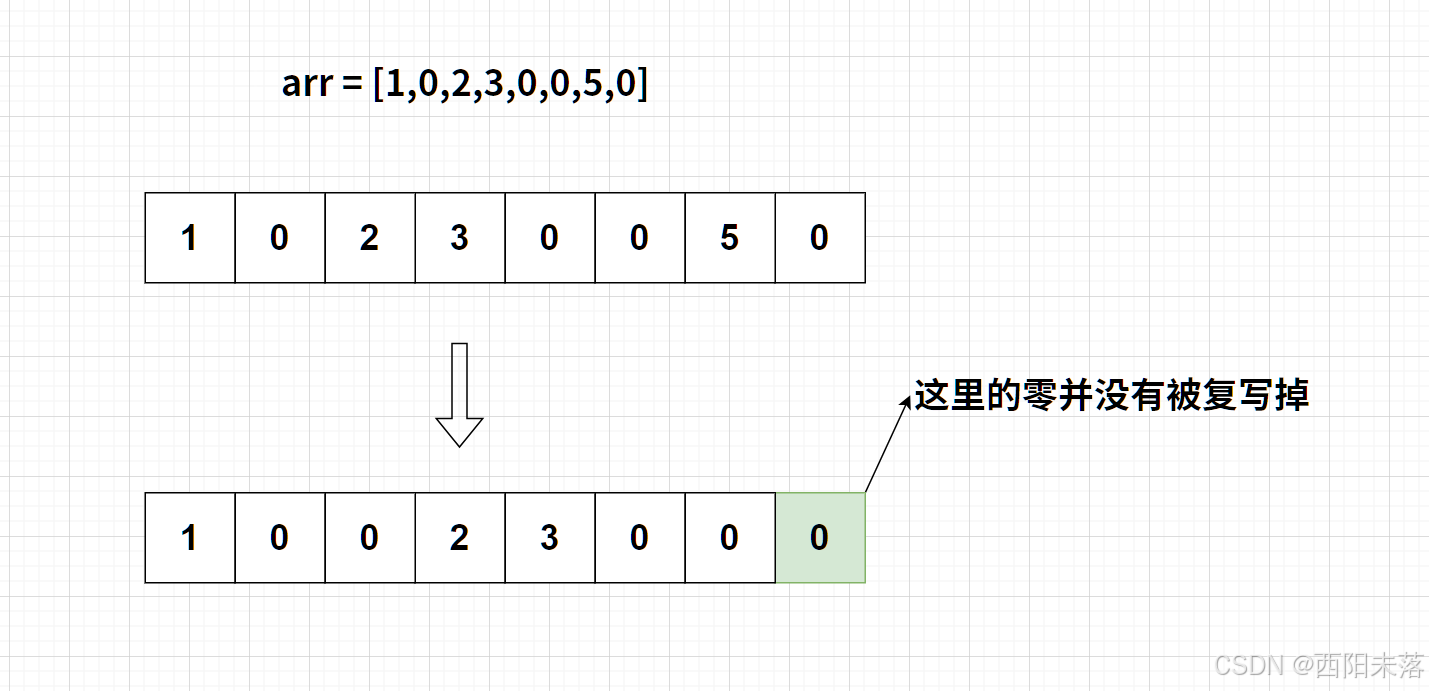
1、其实我们这里比较中要的就是对于特殊情况的判断(一开始就是这里错了),我们要对复写的情况进行判断,这里有两种情况
第一种情况:
就是我们的所有的零都是可以复写,我们这里的情况还是很好理解的,就是示例中写的样子。
第二种情况:
这里也是比较容易忽略的情况,我们这里在示例一上面改进给出我们的图示:
2、我们这里的思路就是找到我们复写后数组的最后一个元素复写前的下标,这里我们实现的时候就是使用的我们的双指针算法,定义两个指针一个指针i用来遍历和找最后一个值的下标,一个指针cnt用来终止遍历,逻辑如下:
a、如果遍历到了0,那么我们cnt指针就++(表示需要复写),然后我们的i和cut指针都++。
b、如果遍历到的不是,那么我们就然i和
cut++。3、经过了2步骤的遍历之后,我们的i -
1指向的就是我们要的最后一个值的下标,同时我们可以通过cut是不是等于n来判断是不是有我们第二种情况(cut等于n说明结果数组中的零都是复写了的,cut不等于n就是要大于n表示我们的第二种情况有一个零要超出范围)。
4、我们接下来就可以进行我们的数组复写操作了,我们这里从i - 1开始遍历,这里也是有两种情况:
a、如果遇到的是非零数或是我们上面第二种情况中绿色部分的数字,我们这个时候就将该值放在我们的数组后边,然后尾指针前移。
b、如果遇到的是零,我们就将两个零放在尾部。
实现代码
cpp
class Solution {
public:
void duplicateZeros(vector<int>& arr) {
int n = arr.size();
int cnt = 0;
int i = 0;
for(; i < n && cnt < n; i++, cnt++) {
if(arr[i] == 0) {
cnt++;
}
}
bool flag = false;
if(cnt == n) {
flag = true;
}
int k = i - 1;
for(int j = k; j >= 0 && n >= 0; j--) {
if(arr[j] || (j == k && !flag)) {
if(n > 0)
arr[--n] = arr[j];
}else {
if(n > 0)
arr[--n] = 0;
if(n > 0)
arr[--n] = 0;
}
}
}
};版本二
其实我们这里的版本二和我们的版本一并没有什么本质上的区别,只是在一些边界条件处理的地方有一些不同,实现思路如下:
1、初始化好两个指针cur = 0, dest = 0;
2、找到最后一个复写的数:
当cur < n的时候,执行下面的循环: a、判断cur位置的元素,如果是0的话,dest往后移动两位否则dest移动一位。
b、判断dest是不是到了结束的位置,是的话就结束循环,如果没有结束那么就cur++继续判断即可。
3、判断dest是不是已经越界了(也就是dest == n),如果是的话,我们n -
1位置的值就设置成为0,cur--,dest往前移动两步(和上面的不同就是这里是将我们的第二种情况直接单独考虑了,后续就不用管了)。
4、从cur位置往后开始遍历数组,然后复写出结果数组:
a、判断cur位置的值,如果是0的话,就在dest和dest - 1位置设置成0;不是0的话我们就直接给我们的cur位置的值即可。
b、cur--,开始下一个位置。
实现代码:
cpp
class Solution {
public:
void duplicateZeros(vector<int>& arr) {
int cur=0,dest=-1,s=arr.size();
while(cur<s)
{
if(arr[cur]) dest++;
else dest+=2;
if(dest>=s-1) break;
cur++;
}
if(dest==s)
{
arr[s-1]=0;
dest-=2;
cur--;
}
while(cur>=0)
{
if(arr[cur]) arr[dest--]=arr[cur--];
else {
arr[dest--]=0;
arr[dest--]=0;
cur--;
}
}
}
};