听课笔记CSAPP

概述：这里是csapp2015 fall 听课中的一些笔记。

lecture2

二进制中位的下标，构成的集合

例如：01101001 ,从右到左边下标从0 ~ 7，其中值为 1 的有，{0，3，5，6}，这些下标构成一个集合。

下面我们看看这个集合的一些运算，首先给出两个二进制数字如下 a = 0b01101001 和 b= 0b01010101;

将这两数字映射为集合得到 a1 = {0，3，5，6} 和 b1 = {0，2，4，6}

依此类推：可以得到 | 对应集合中的 并运行 ; ^ 得到两个集合中不同的部分；~ 取补集

位移

只有一种左移，但是有两种右移，分为逻辑右移和算术右移。

左移：低位补0

逻辑右移：高位补0

算术右移：高位补符号位

数字范围

无符号数： 0 ~ 2w−12^w -12w−1

Two's complement : −22−1-2^{2-1}−22−1 ~ 22−1−12^{2-1}-122−1−1

下面这张ppt将映射关系画了出来：

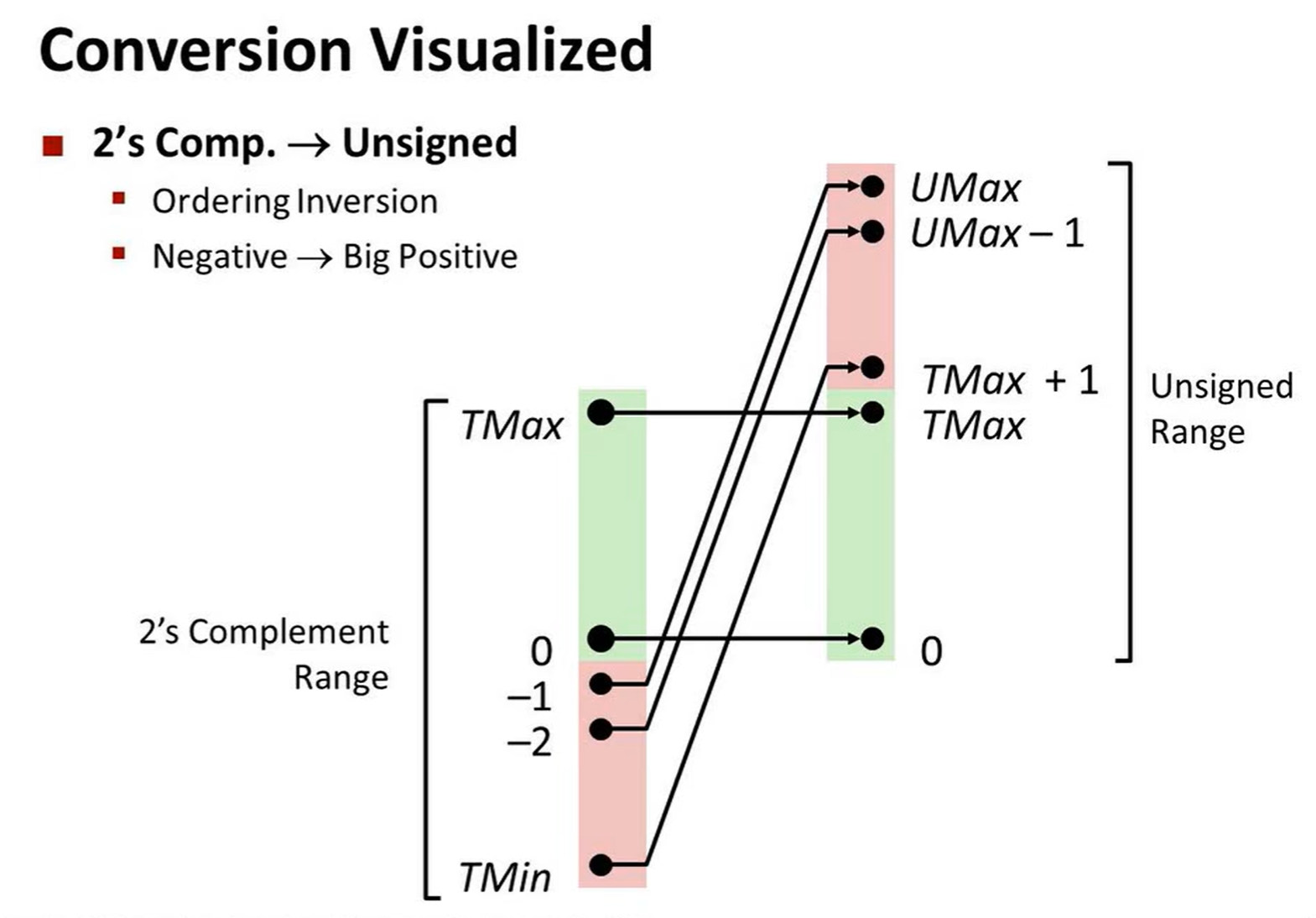
注意：运算中有一个是无符号数，那么另外一个数也会转换成无符号数进行比较，<,>,==,<=,>= 这些符号如果使用不当，会有意外的bug出现。

∣TMax∣+1=∣TMin∣ |TMax| + 1 = |TMin| ∣TMax∣+1=∣TMin∣
UMax=2TMax+1 UMax = 2 TMax + 1 UMax=2TMax+1

第一个公式，可以看出在补码中的数字表示是不对称的，因为有0的存在；

第二个公式，从原理上理解会清晰，TMax的最高位（符号位）不是1，其余位都是0，UMax是全部为1；2TMax将二进制数字向左移动了一位，+1 是为了将移出来后最低位的0变成1.

bug

c 复制代码

int i;
for(int i=n-1;i-sizeof(char)>=0;i--)
	f(a[i]);

sizeof 返回的 unsigned 类型，运算会自动转换成 unsigned，然后会一直大于0，这样这就是一个死循环。

扩展/截断位数

无符号数，扩展的时候，高位补0；补码在扩展的时候，高位补符号位；

为什么高位补符号位会对数字的大小没有影响？

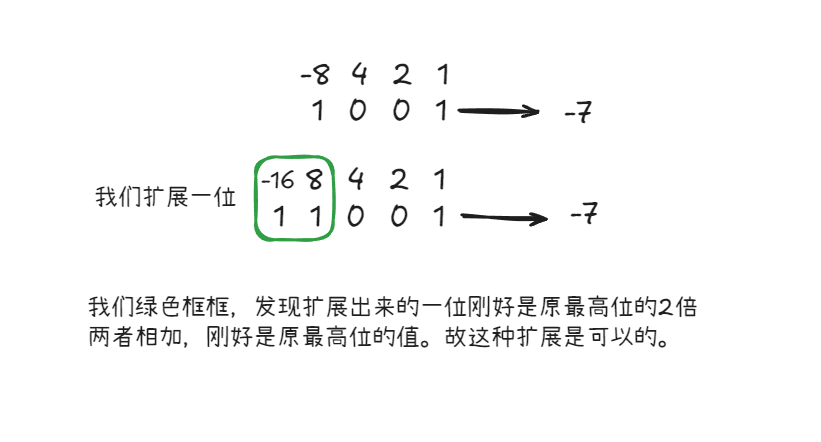
扩展一位是这样，扩展多位的时候，依次类推就好。

我们基于这样的原理，能得到很好的结论，当我们看到一堆类似ffff...0123 前面的一堆f只是想告诉我们这是一个负数。

截断

无论是无符号数还是补码，当截去最高位的时候，值的变化都相当于减去最高位。

但是补码有一种情况下是值不变的，那就是最高位为1，最高位的下一位也是1的时候。

大家可以想想为什么？

lecture3

算术溢出

无符号数溢出 ： x+y−2wx+y-2^wx+y−2w

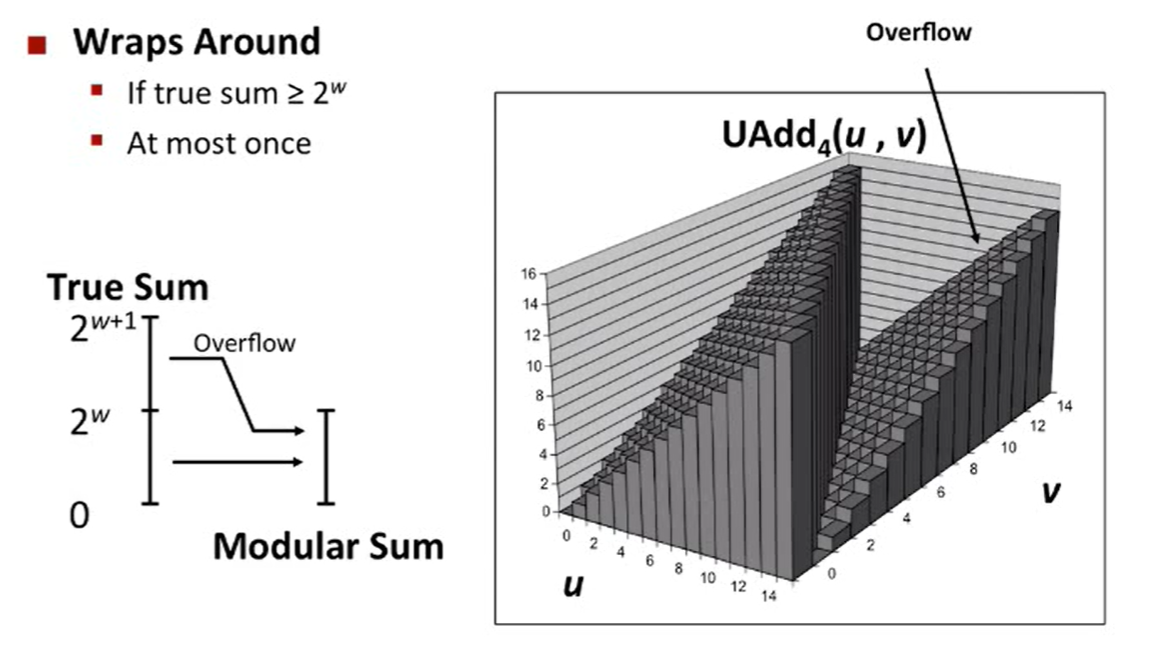
补码溢出：分为正溢出和负溢出

正溢出：x+y−2wx+y-2^wx+y−2w

负溢出：x+y+2wx+y+2^wx+y+2w

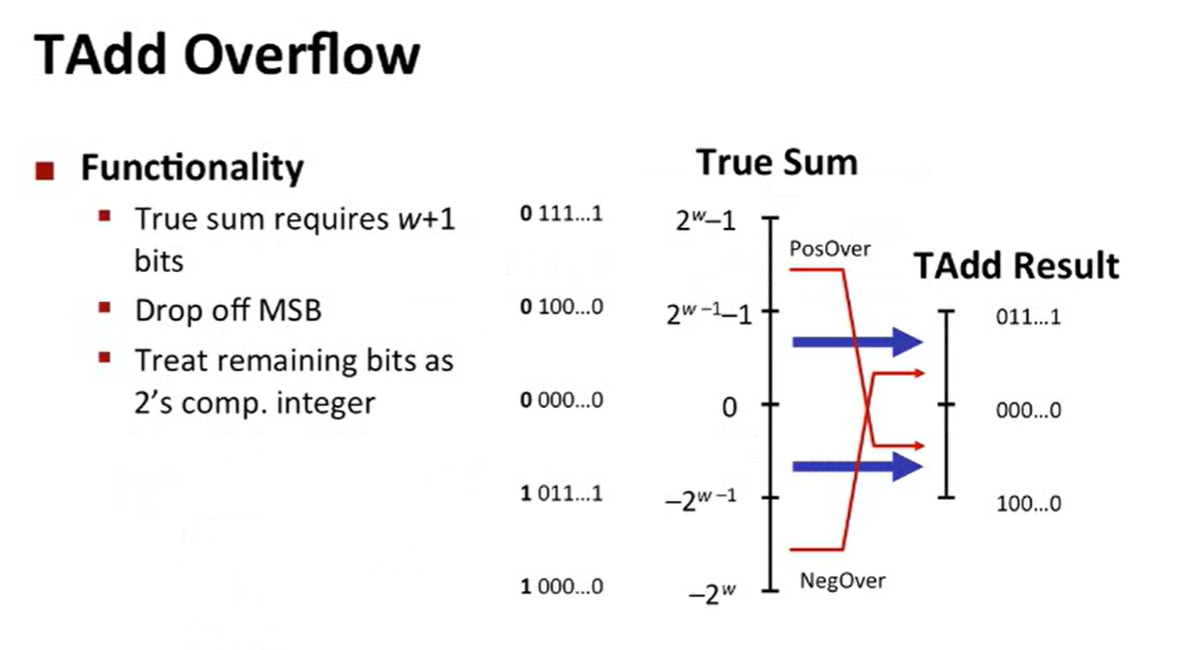
总结：无论是什么数字的溢出，在编码级别的处理方法都是将溢出位丢弃，然后保留剩下的。

位移运算

我们知道，c语言中的位移运算，左移相当于乘2 , 右移相当于除以2；下面将给出相应的数学公式

二进制的表示：x=∑i=0w−1xi2i 二进制的表示： x = \sum_{i=0}^{w-1}x_i2^i \newline 二进制的表示：x=i=0∑w−1xi2i

我们左移的时候，相当于2i2^i2i权重变成了2i+12^{i+1}2i+1

左移一位：x=∑i=0w−1xi2i+1=2∑i=0w−1xi2i左移一位： x = \sum_{i=0}^{w-1}x_i2^{i+1} = 2 \sum_{i=0}^{w-1}x_i2^i左移一位：x=i=0∑w−1xi2i+1=2i=0∑w−1xi2i

右移同理的操作，但不是所有的整数都可以被2整除，那么不能被2整除的数字怎么办呢？

这里给出结论，会直接将小数部分舍去（正数的实现，大家用笔画画很好就能推出来）。

负数的实现，需要加一个偏置，来达到这个效果。

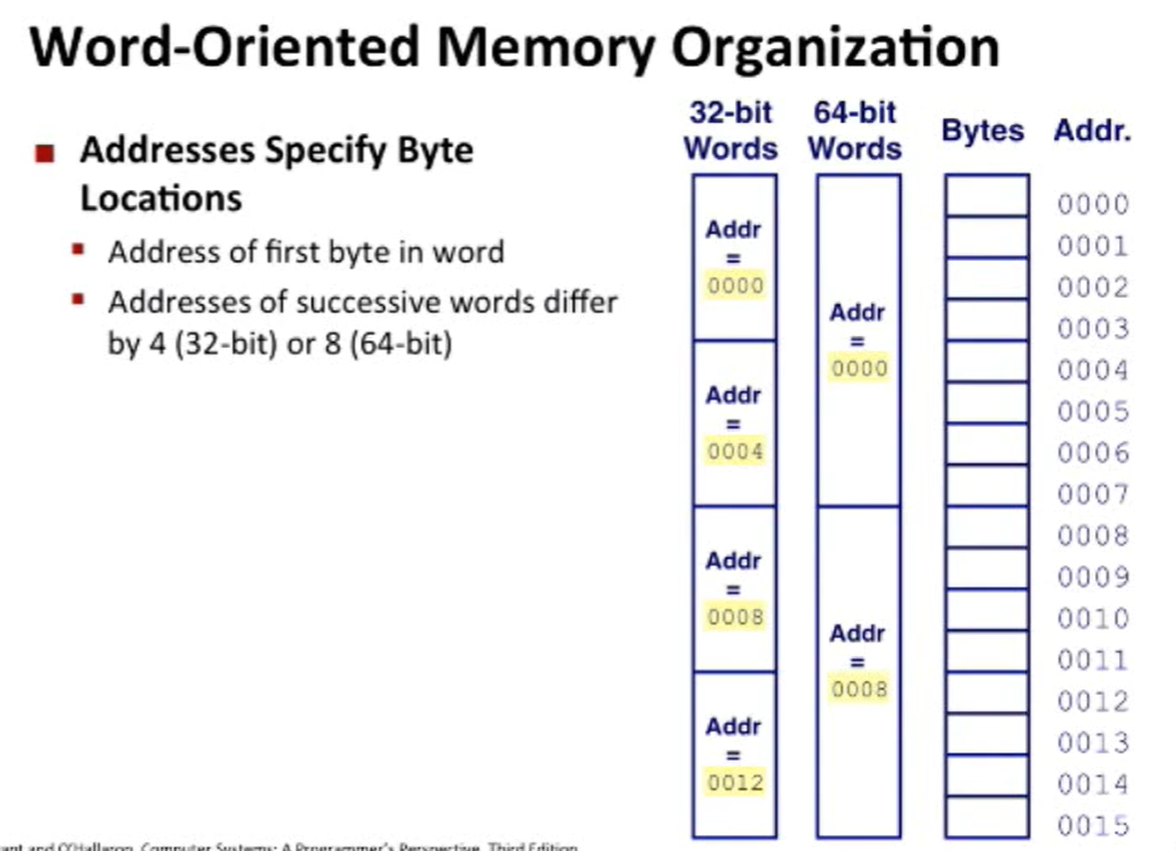
内存

c 复制代码

#include<stdio.h>

typedef unsigned char *pointer;

void show_bytes(pointer start,size_t len){
        size_t i;
        for(i = 0;i<len;i++){
                printf("%p\t 0x%.2x\n",start+i,start[i]);
        }

}


int main(){
        size_t i;
        printf("%ld\n",sizeof(i));

        int a = 15213;
        printf("%d\n",a);
        show_bytes((pointer) &a,sizeof(int));

        return 0;

}

输出：

复制代码

8
15213
0x7ffd50303324   0x6d
0x7ffd50303325   0x3b
0x7ffd50303326   0x00
0x7ffd50303327   0x00

字节顺序

字节顺序分为：大端法和小端法，具体表示如图

![[PixPin_2025-10-09_13-27-13.png]]

网络协议一般使用：大端法；

硬件目前主流为：小端法；

lecture4

IEE Standard

(−1)sM2E (-1)^s M2^E (−1)sM2E

其中 s 是符号位，M 是底数，E 是指数

公式和上图的二进制的表示对应s = s ; E != exp ; M != frac;

我们先来讨论规格化的浮点数，即 exp != 00...00 && exp != 11...11

E=exp−Bias(偏置值) E = exp - Bias(偏置值) E=exp−Bias(偏置值)
Bias=2k−1−1 Bias = 2^{k-1} - 1 Bias=2k−1−1

注：k为指数域的宽度。

M=1.fracM = 1.frac M=1.frac

例子：

![[Pasted image 20251009174714.png]]

上面聊完了规格化，下面再看看非规格化的情况

注：非规格化用来表示极小值的规则，当 exp = 000...0000

E=1−BiasE = 1 - BiasE=1−Bias

为什么指数变成了这样，我们在后面会说明。

M=0.fracM = 0.frac M=0.frac

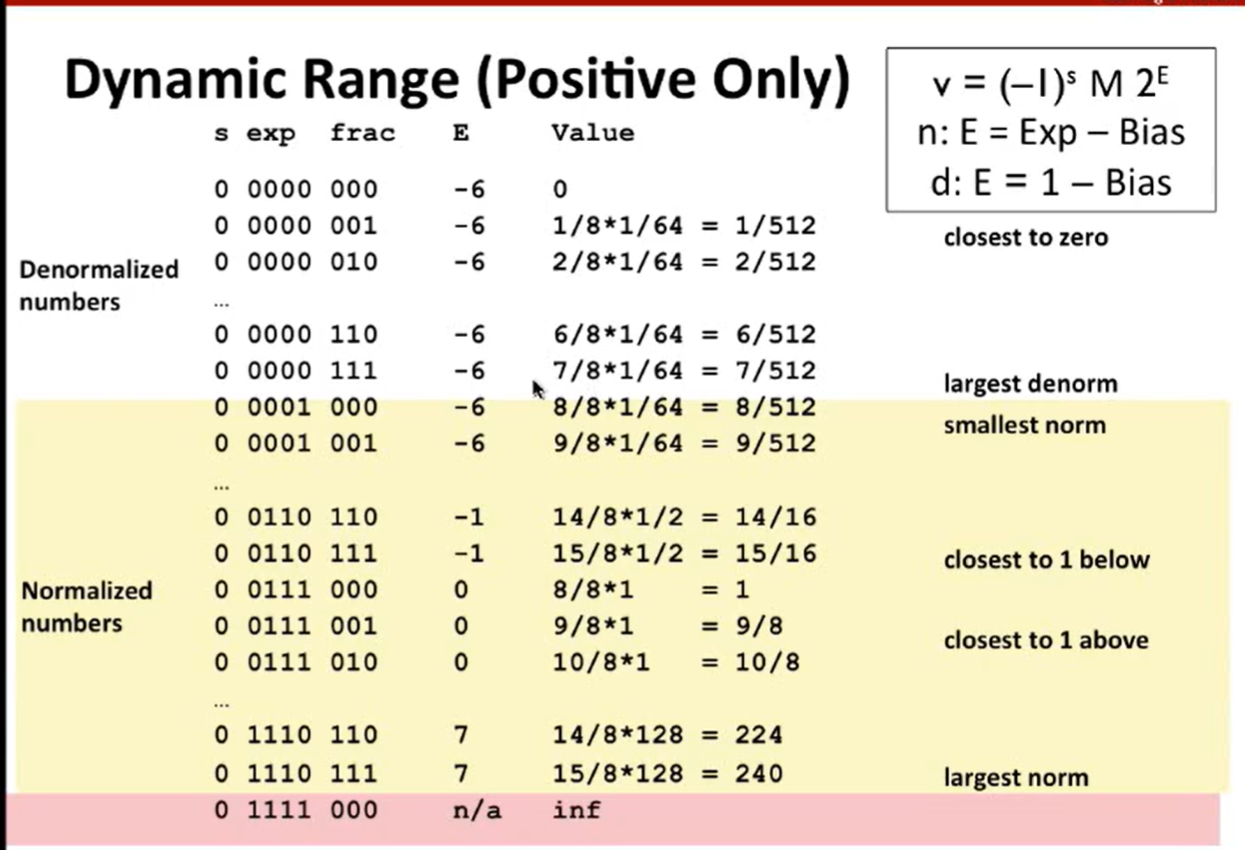
通过这张图，我们可以看到非规格化的的最大值和规格化的最小值平滑的过度了。

这归功于我们对于 E 和 M 的操作。

舍入

在二进制中，默认的舍入方式是，小于一半就舍，超过一半就入，中间值让其舍入变成偶数

下面举一些例子