3 三层神经网络的构建与实现
三层感知机的 "三层" 指权重计算层的数量,对应的神经元层结构为:
输入层(第0层)→ 隐藏层1(第1层)→ 隐藏层2(第2层)→ 输出层(第3层)
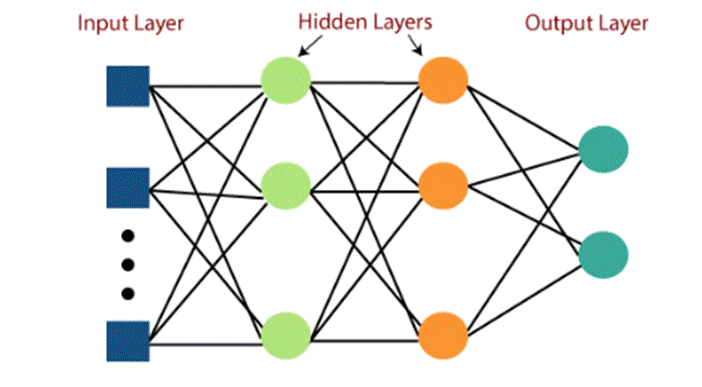
图 10三层神经网络
在实际应用中,三层神经网络虽然结构简单,但在许多任务上都能取得良好的性能。例如,在 MNIST 手写数字识别任务中,三层感知机可以达到 97% 以上的识别准确率。
更重要的是,理解三层神经网络的原理是学习更复杂深度学习架构的基础。无论是卷积神经网络(CNN)、循环神经网络(RNN)还是 Transformer,其核心思想都可以追溯到三层神经网络。
三层神经网络的架构设计需要考虑以下几个关键要素:
输入层设计:输入层的神经元数量由输入数据的特征维度决定。对于 MNIST 手写数字识别任务,每张图像是 28×28 像素的灰度图像,因此输入层需要 784 个神经元,每个神经元对应一个像素值。输入层的作用是接收原始数据并将其传递给隐藏层,本身不进行任何计算。
隐藏层设计:隐藏层是三层神经网络的核心,负责对输入数据进行非线性变换和特征提取。隐藏层神经元数量的选择对模型性能有重要影响。根据经验规则,隐藏层神经元数量应在输入层大小和输出层大小之间,通常可以设置为输入层大小的 2/3 加上输出层大小的 2/3,或小于输入层大小的两倍。对于 MNIST 任务,隐藏层通常设置 100-256 个神经元。
输出层设计:输出层的神经元数量由任务的类别数决定。对于 MNIST 手写数字识别,需要识别 0-9 共 10 个数字,因此输出层设置 10 个神经元。输出层的激活函数通常采用 Softmax 函数,将原始输出转换为概率分布,便于进行分类预测。
三层神经网络的工作原理可以分为两个阶段:
前向传播阶段:输入信息从输入层经隐含层逐层计算传向输出层。在这个过程中,每一层的神经元接收来自前一层神经元的输出作为输入,通过加权求和和激活函数处理后,将结果传递给下一层。具体而言,隐藏层的第 j 个神经元的激活值 aⱼ² = σ(∑ᵢ wⱼᵢ¹aᵢ¹ + bⱼ²),输出层的第 k 个神经元的激活值 aₖ³ = σ(∑ⱼ wₖⱼ²aⱼ² + bₖ³),其中 σ 是非线性激活函数。
反向传播阶段:如果输出层没有得到期望的输出,则计算输出层的误差变化值,然后将误差信号沿原来的连接通路反传回来修改各层神经元的权值。反向传播算法基于链式法则,通过逐层计算误差对各层权重和偏置的偏导数,实现对网络参数的优化。
下面为三层感知机的预定义统一符号:
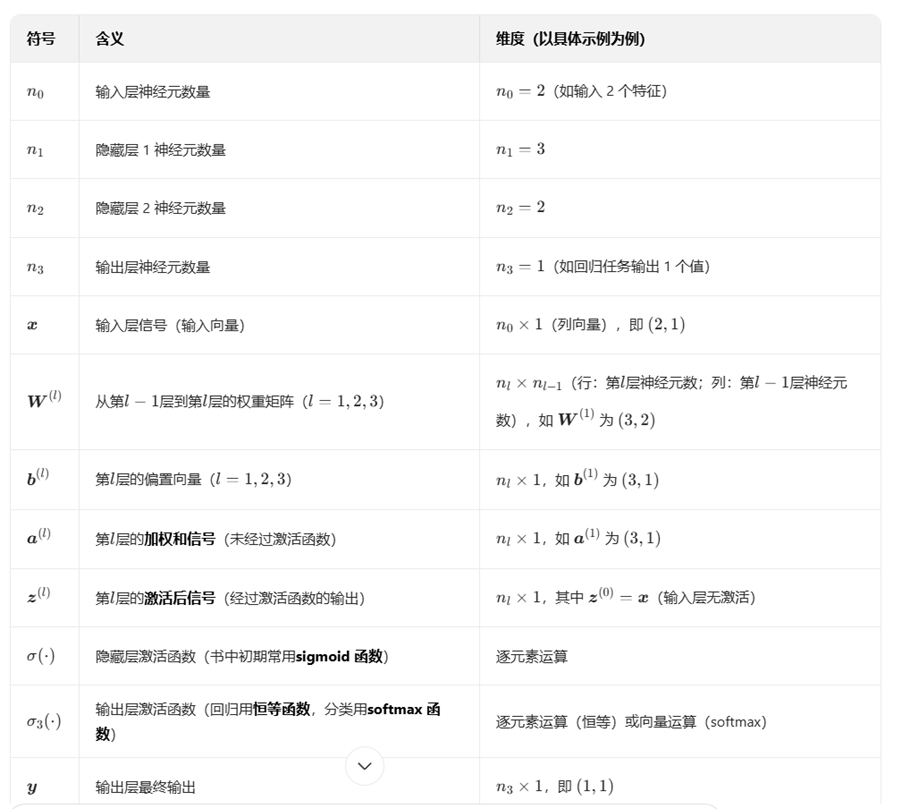
图 11统一符号
三层感知机前向传输的核心逻辑是:信号从输入层开始,经每一层的 "加权和→激活函数" 变换后,逐层传递至输出层。
1)第一步:输入层 → 隐藏层 1 的信号传递
输入层无激活函数,其输出直接作为隐藏层 1 的输入,即
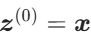
(1)计算隐藏层 1 的加权和
隐藏层 1 的每个神经元会接收输入层所有神经元的信号,并与对应权重相乘后求和,再加上自身偏置:
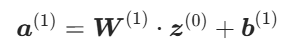
(2)计算隐藏层 1 的激活输出
为引入非线性变换(打破线性模型的局限性),需将加权和输入激活函数(在此选用sigmoid 函数)
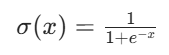
因此,隐藏层 1 的激活输出为:
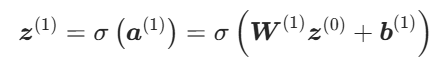
性质:sigmoid 函数将输入压缩到 \((0,1)\) 区间,为网络引入非线性,是三层感知机能够近似复杂函数的关键
2) 第二步:隐藏层 1 → 隐藏层 2 的信号传递
与 "输入层→隐藏层 1" 逻辑完全一致,隐藏层 1 的激活输出作为隐藏层 2 的输入。
(1)计算隐藏层 2 的加权和
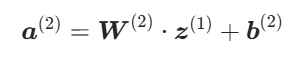
(2)计算隐藏层 2 的激活输出
仍使用 sigmoid 激活函数:
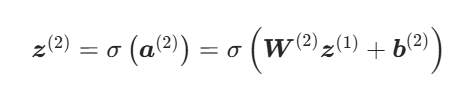
3)第三步:隐藏层 2 → 输出层的信号传递
输出层的目标是根据任务输出最终结果,因此激活函数需适配任务类型(与隐藏层的 sigmoid 不同)。
(1)计算输出层的加权和
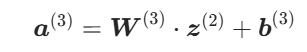
(2)计算输出层最终输出
根据任务选择激活函数:
回归任务(如预测房价):用恒等函数(输出与加权和一致)。
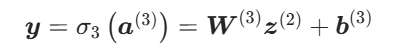
分类任务(如二分类 / 多分类):用softmax 函数(输出概率分布),即:
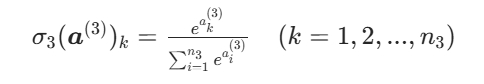
此时 输出的每个元素表示对应类别的概率,且所有元素和为 1。
Softmax 函数具有以下特点:
- 输出向量中的每个元素都在 (0,1) 之间
- 所有元素的和为 1,可以解释为概率
- 指数函数的使用使得较大的输入值对应的输出概率更大,具有 "放大" 效应