背景 牧师-村名模型
n个牧师去城市布道,随意选择n个布道点,并把这n个点公告诉所有村民
每个村民选择到离自己家最近的布道点去听课,听课后,有的人会觉得距离太远
于是每个牧师统计自己课上所有村民的地址,然后搬到这些地址的中心地带,并把新的步道点告诉所有村名
每个村民选择到离自己家最近的布道点去听课(比如之前去牧师A处,现在发现去牧师B处更近)
牧师每次课后都会更新位置,村民根据情况选择布道点,最终经历若干礼拜后,布道点终于稳定下来
步骤
选择某种距离作为数据样本间的相似性度量
根据实际需要选择不同的距离:欧式距离、曼哈顿距离、绝对值距离、切比雪夫距离等
作为样本间的相似性度量,最常用的是欧式距离

质心的含义:

复杂度
伪代码:
获取数据 n 个 m 维的数据
随机生成 K 个 m 维的点
while(t)
for(int i=0;i < n;i++)
for(int j=0;j < k;j++)
计算点 i 到类 j 的距离
for(int i=0;i < k;i++)
1. 找出所有属于自己这一类的所有数据点
2. 把自己的坐标修改为这些数据点的中心点坐标
end
优缺点
优点
容易理解,聚类效果不错,虽然是局部最优, 但往往局部最优就够了
处理大数据集的时候,该算法可以保证较好的伸缩性
当簇近似高斯分布的时候,效果非常不错
算法复杂度低
缺点
K 值需要人为设定,不同 K 值得到的结果不一样
对初始的簇中心敏感,不同选取方式会得到不同结果
对异常值敏感
样本只能归为一类,不适合多分类任务
不适合太离散的分类、样本类别不平衡的分类、非凸形状的分类
算法调优与改进
针对算法的缺点,有多种调优方式:如数据预处理(去除异常点),合理选择 K 值,高维映射等
数据预处理
K-means 的本质是基于欧式距离的数据划分算法,均值和方差大的维度将对数据的聚类产生决定性影响
所以未做归一化处理和统一单位的数据是无法直接参与运算和比较的
常见的数据预处理方式有:数据归一化,数据标准化
此外,离群点或者噪声数据会对均值产生较大的影响,导致中心偏移,因此还需要对数据进行异常点检测
合理选择 K 值
K 值的选取对 K-means 影响很大,这也是 K-means 最大的缺点
常见的选取 K 值的方法有:手肘法、Gap statistic 方法
手肘法 (Elbow Method)
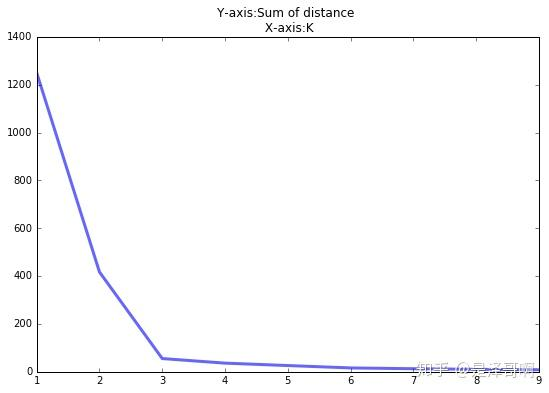
用于确定最优聚类数 K 的直观方法,核心逻辑是通过分析 "聚类数 K 与类内总距离和(SSE)" 的关系,找到聚类效果由 "快速提升" 转向 "缓慢提升" 的临界点(形似手肘的拐点)


优点:
直观易操作,无需领域先验知识,仅通过数据自身的 SSE 变化即可判断
缺点:
对 "手肘点" 的判断具有主观性(不同人可能对拐点的认知不同);当数据分布复杂时,可能不存在明显的手肘点,或存在多个模糊拐点。
除手肘法外,还可采用轮廓系数法(分析类内紧凑度与类间分离度的平衡)、Gap 统计量(对比实际 SSE 与随机数据的 SSE 差异)等方法,可结合场景选择或交叉验证。
当 K < 3 时,曲线急速下降;当 K > 3 时,曲线趋于平稳,通过手肘法我们认为拐点 3 为 K 的最佳值
手肘法的缺点在于需要人工看,不够自动化,所以有了 Gap statistic 方法(出自斯坦福大学的几个学者的论文:Estimating the number of clusters in a data set via the gap statistic)
Gap统计(Gap statistic)
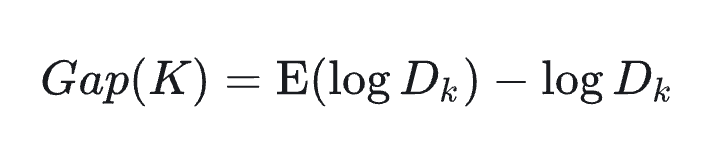


Gap 统计量的核心逻辑是:比较实际数据的聚类紧凑度与 "无结构随机数据" 的聚类紧凑度。
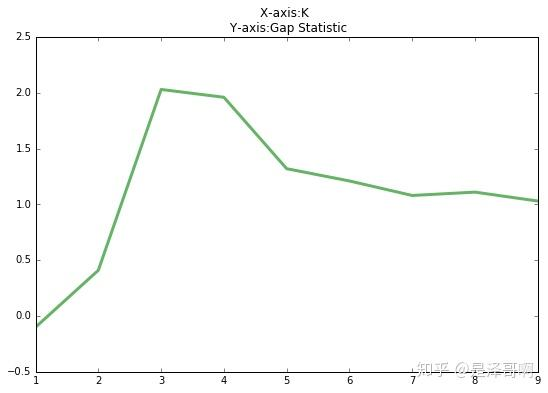
当 Gap(K) 达到最大时,对应的 K 即为最优聚类数。
它解决了手肘法 "拐点判断主观" 的问题:
通过引入随机参考分布,更客观地评估聚类数的合理性,尤其适用于数据分布复杂、手肘点不明显的场景。

由图可见,当 K=3 时,Gap(K) 取值最大,所以最佳的簇数是 K=3。
Github 上一个项目叫 gap_statistic ,可以更方便的获取建议的类簇个数。
示例

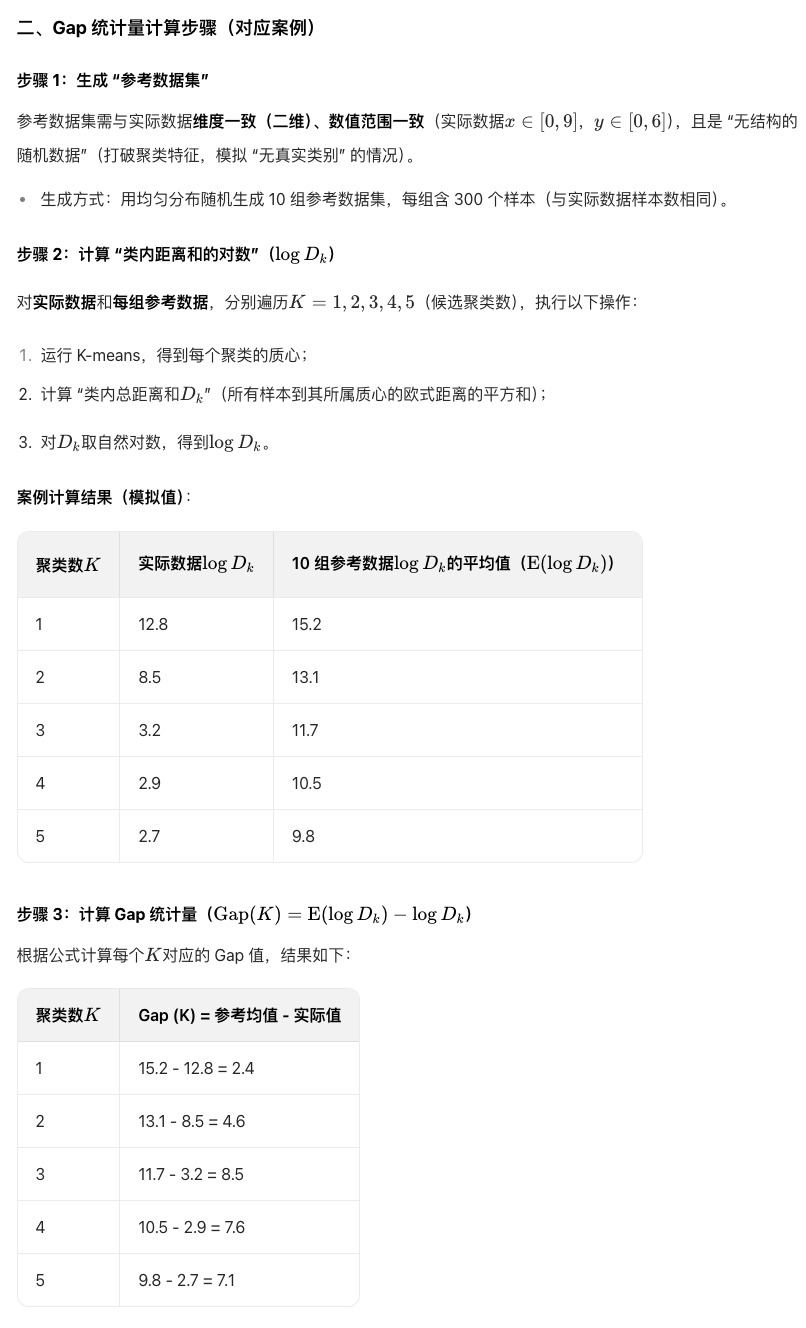


公式这么设计的背景:

采用核函数
基于欧式距离的 K-means 假设了了各个数据簇的数据具有一样的的先验概率并呈现球形分布,但这种分布在实际生活中并不常见。
面对非凸的数据分布形状时我们可以引入核函数来优化,这时算法又称为核 K-means 算法,是核聚类方法的一种。
核聚类方法的主要思想是通过一个非线性映射,将输入空间中的数据点映射到高位的特征空间中,并在新的特征空间中进行聚类。
非线性映射增加了数据点线性可分的概率,从而在经典的聚类算法失效的情况下,通过引入核函数可以达到更为准确的聚类结果。
K-means++
初始值的选取对结果的影响很大,对初始值选择的改进是很重要的一部分。在所有的改进算法中,K-means++ 最有名。

ISODATA
ISODATA 的全称是迭代自组织数据分析法。它解决了 K 的值需要预先人为的确定这一缺点。
而当遇到高维度、海量的数据集时,人们往往很难准确地估计出 K 的大小。
ISODATA 就是针对这个问题进行了改进,它的思想也很直观:
当属于某个类别的样本数过少时把这个类别去除,当属于某个类别的样本数过多、分散程度较大时把这个类别分为两个子类别。
附录
欧式距离

应用场景有
- 机器学习:用于 K - 均值聚类(衡量样本与聚类中心的相似度)、K 近邻算法(判断样本间的 "远近")、降维算法(如 PCA 中衡量数据的离散程度)。
- 地理信息:计算两地的直线距离(忽略地形、道路等实际障碍)
- 数据分析:衡量两个向量(如用户画像、特征向量)的 "差异程度"
优点:
该距离直观易理解,数学性质稳定,是 "距离" 的经典定义
缺点:
对量纲敏感(若不同维度的数值范围差异大,会被数值大的维度主导),且未考虑特征间的相关性。
因此,在部分场景中需先对数据做标准化(如 Z-score 归一化),或改用马氏距离等改进方法
为什么 K-means 不适合 "太离散的分类"
K-means 的核心假设是"类内样本紧凑、类间样本分离",通过 "最小化类内距离和" 来优化聚类中心。
若样本过于离散(类内样本分布松散,距离聚类中心很远),K-means 会强行将它们归为一类,导致类内方差极大,违背 "紧凑聚类" 目标。
例如:若一类样本在空间中呈 "散点" 分布,K-means 计算的质心可能位于样本的 "空区域",无法真正代表该类特征,聚类结果非常模糊。
为什么 K-means 不适合 "样本类别不平衡"
K-means 对样本数量差异大的类别 "天然偏心",原因在于其优化目标是 "最小化所有样本到所属聚类中心的距离和"。
若某类样本数量极少(如 10 个),另一类极多(如 1000 个),K-means 会倾向于将聚类中心向数量多的类别偏移(因为大量样本的距离和对总损失影响更大)。
结果:少数类会被 "吞噬" 或聚类中心严重偏离,导致类别边界模糊,甚至少数类直接被错误归类。
为什么 K-means 不适合 "非凸形状的分类"
K-means 的聚类边界是 "以聚类中心为圆心的超球面"(二维中是圆,三维中是球),仅能处理凸形状的类别(如圆形、球形簇)。
若类别是非凸形状(如环形、月牙形、不规则形状),K-means 的 "球面边界" 无法贴合类别轮廓。
例如:若一类样本呈 "环形" 分布,K-means 的质心会落在环的中心(空区域),导致环上的样本被错误地分到其他类,或被强行归为一类(完全破坏原有形状)。
K-means 的本质局限
K-means 基于 "质心 + 欧式距离 + 类内紧凑性"的假设,这使其在面对离散分布、类别不平衡、非凸形状时,无法捕捉数据的真实结构,最终导致聚类结果失真。
若需处理这类场景,可考虑改用密度聚类(如 DBSCAN)(适合非凸、离散分布)、层次聚类(对类别不平衡更鲁棒)或基于高斯混合模型的聚类(适合非球形簇)等方法。