《C++二叉引擎：STL风格搜索树实现与算法优化》

chenyuhao20242025-10-13 11:27

前言**：**二叉搜索树（Binary Search Tree, BST）是计算机科学中最基础且强大的数据结构之一，它凭借 O(log n) 的平均查找、插入和删除效率，成为高效数据管理的关键工具。在C++中，BST不仅是标准模板库（STL）std::set 和 std::map 的底层实现基础，更是理解更高级数据结构（如AVL树、红黑树）的必经之路。

目录

一、二叉搜索树介绍

二、二叉搜索树的实现

结构创建

插入节点

​编辑

中序遍历

查找节点

删除节点

三、二叉树的应用

K模型

KV模型

KV代码实现

一、二叉搜索树介绍

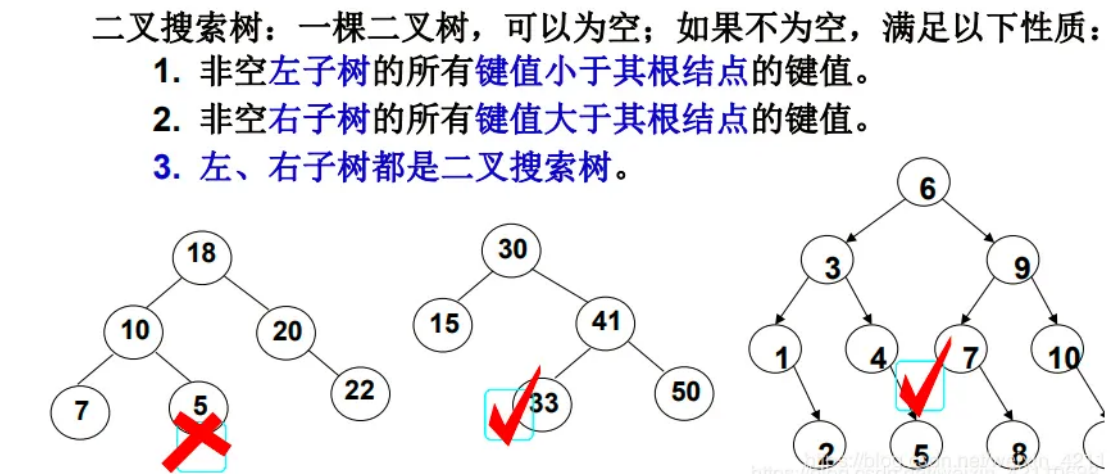
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

  • 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
  • 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
  • 它的左右子树也分别为二叉搜索树

二、二叉搜索树的实现

这个模块，我们会从结构构建到增删查改，一步步演示二叉搜索树的搭建过程。

结构创建

实现一棵二叉搜索树，我们需要一个节点结构、一个功能结构

其中节点结构里面有左右子节点（left，right）、一个数据存储变量（date）：

cpp 复制代码 
//节点结构
template<class T>
struct Tree_Node
{
	Tree_Node(const T _date)
		:left(nullptr)
		,right(nullptr)
		,date(_date)
	{ }
	Tree_Node<T>* left;
	Tree_Node<T>* right;
	T date;
};

功能结构用来实现二叉搜索树的功能：

cpp 复制代码 
//功能结构
template<class T>
class BST
{
	typedef Tree_Node<T> Node;
public:
	//构造
	BST()
		:node(nullptr)
	{ }
 
	//功能实现
 
private:
	Node* node;
};

插入节点

插入操作的简述：

  1. 先从根节点开始搜索插入位置：
  2. 若目标值小于当前节点值，则向当前节点的左子树移动；若目标值大于当前节点值，则向当前节点的右子树移动
  3. 当到达叶子节点时，根据目标值与叶子节点值的大小关系，将新节点作为叶子节点的左子节点或右子节点插入

平均时间复杂度为 O(logn)，最坏时间复杂度为O(n)

插入节点我们需要根据数据的大小来判断插在左右节点的 nullptr 位置，我们这里用循环来写更容易理解：

cpp 复制代码 
 // 插入节点（非递归）
 void Insert(const T& date) {
     // 如果根节点为空
     if (root == nullptr) {
         root = new Node(date);
         return;
     }

     // 根据数据大小查找插入位置
     Node* parent = nullptr;
     Node* cur = root;
     while (cur) {
         parent = cur;  // 记录父节点
         if (date < cur->date) {
             cur = cur->left;   // 向左子树查找
         }
         else if (date > cur->date) {
             cur = cur->right;  // 向右子树查找
         }
         else {
             return;  // 数据已存在，直接返回
         }
     }

     // 创建新节点并插入
     if (date < parent->date) {
         parent->left = new Node(date);  // 插入左侧
     }
     else {
         parent->right = new Node(date); // 插入右侧
     }

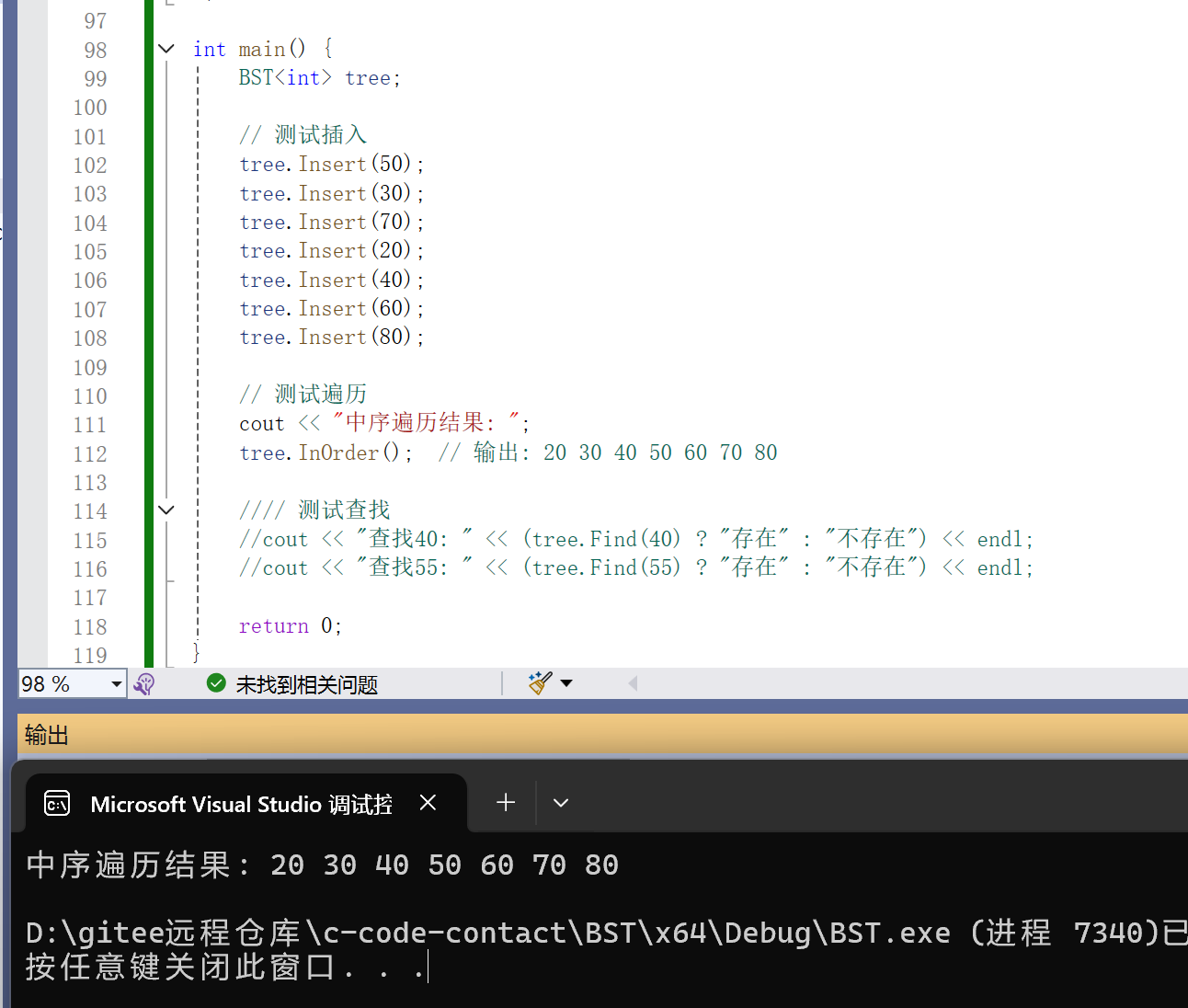
中序遍历

cpp 复制代码 
//中序遍历
void Inorder()
{
	_Inorder(node);
}
 记得私有中序遍历辅助函数
void _Inorder(Node* ptr)
{
	//遇到空就返回
	if (ptr == nullptr)
	{
		return;
	}
 
	_Inorder(ptr->left);
 
	cout << ptr->date << " ";
 
	_Inorder(ptr->right);
}

查找节点

cpp 复制代码 
// 查找节点（非递归）
bool Find(const T& date) {
    Node* cur = root;
    while (cur) {
        if (date < cur->date) {
            cur = cur->left;   // 向左查找
        }
        else if (date > cur->date) {
            cur = cur->right;  // 向右查找
        }
        else {
            return true;  // 找到节点
        }
    }
    return false;  // 未找到
}

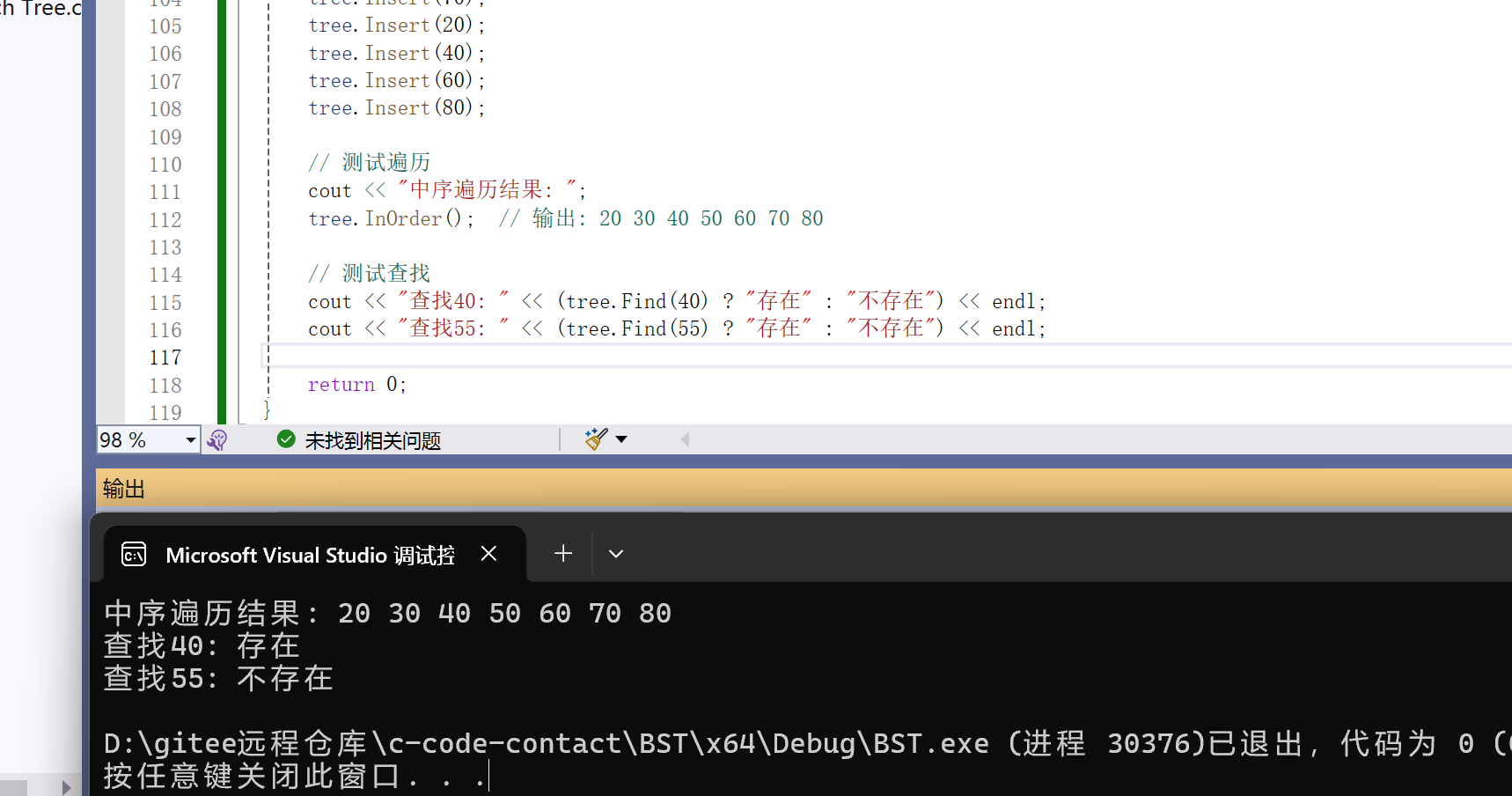
删除节点

首先查找元素是否在二叉搜索树中，如果不存在，则返回, 否则要删除的结点可能分下面四种情 况：

  • 要删除的结点无孩子结点
  • 要删除的结点只有左孩子结点
  • 要删除的结点只有右孩子结点
  • 要删除的结点有左、右孩子结点
    但是我们根据实际来看，这四种情况可以分为三种情况，简单来说
  1. 该节点无孩子节点：先删，然后置空
  2. 该节点有一个孩子节点：先连接再删
  3. 该节点有两个孩子节点：我们需要找一定大小的节点去替代它。

替代思路：让它的左子树最大值或者右子树最小值去替换，然后删除它（左子树max为例）
平均时间复杂度为O(logn)，最坏情况为O(n)

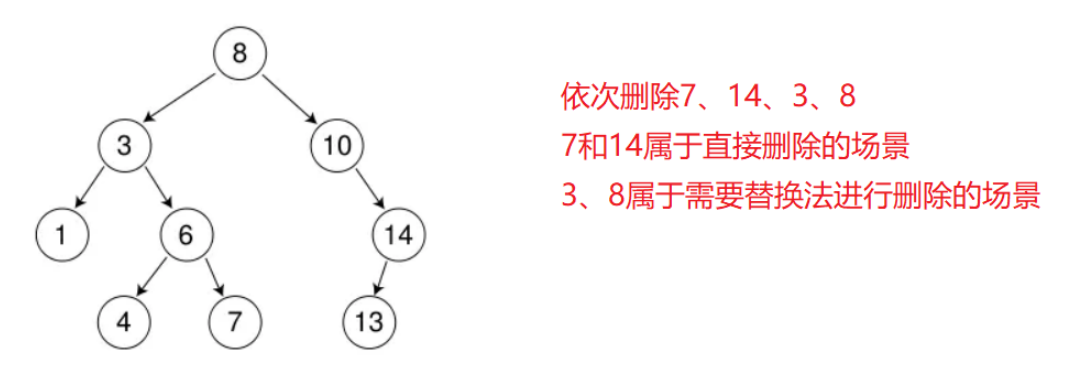
我们这里拿3举个例子：

  1. 先找到目标节点3，然后找目标节点左子树的最大值left_max
  2. 交换目标节点cur和最大值 left_max的数据 ，标记 left_max的父节点为 parent。
    找其左子树中的最大节点，即左子树中最右侧的节点，或者在其右子树中最小的节点，即右子树中最小的节点，替代节点找到后，将替代节点中的值交给待删除节点，转换成删除替代节点。
cpp 复制代码 
// 删除节点（非递归）
    bool Erase(const T& date) {
        Node* parent = nullptr;
        Node* cur = root;
        
        // 查找要删除的节点及其父节点
        while (cur && cur->date != date) {
            parent = cur;
            if (date < cur->date) {
                cur = cur->left;
            }
            else {
                cur = cur->right;
            }
        }
        
        if (cur == nullptr) return false; // 未找到要删除的节点

        // 情况1：删除的节点有两个子节点
        if (cur->left && cur->right) {
            Node* minRight = cur->right;
            Node* minRightParent = cur;
            
            // 找到右子树中的最小节点
            while (minRight->left) {
                minRightParent = minRight;
                minRight = minRight->left;
            }
            
            // 用最小节点的值替换当前节点值
            cur->date = minRight->date;
            
            // 转换为删除minRight（此时minRight最多有一个右子节点）
            cur = minRight;
            parent = minRightParent;
        }

        // 情况2和3：删除的节点有0或1个子节点
        Node* child = cur->left ? cur->left : cur->right;
        
        if (parent == nullptr) { // 删除的是根节点
            root = child;
        }
        else if (parent->left == cur) {
            parent->left = child;
        }
        else {
            parent->right = child;
        }
        
        delete cur;
        return true;
    }

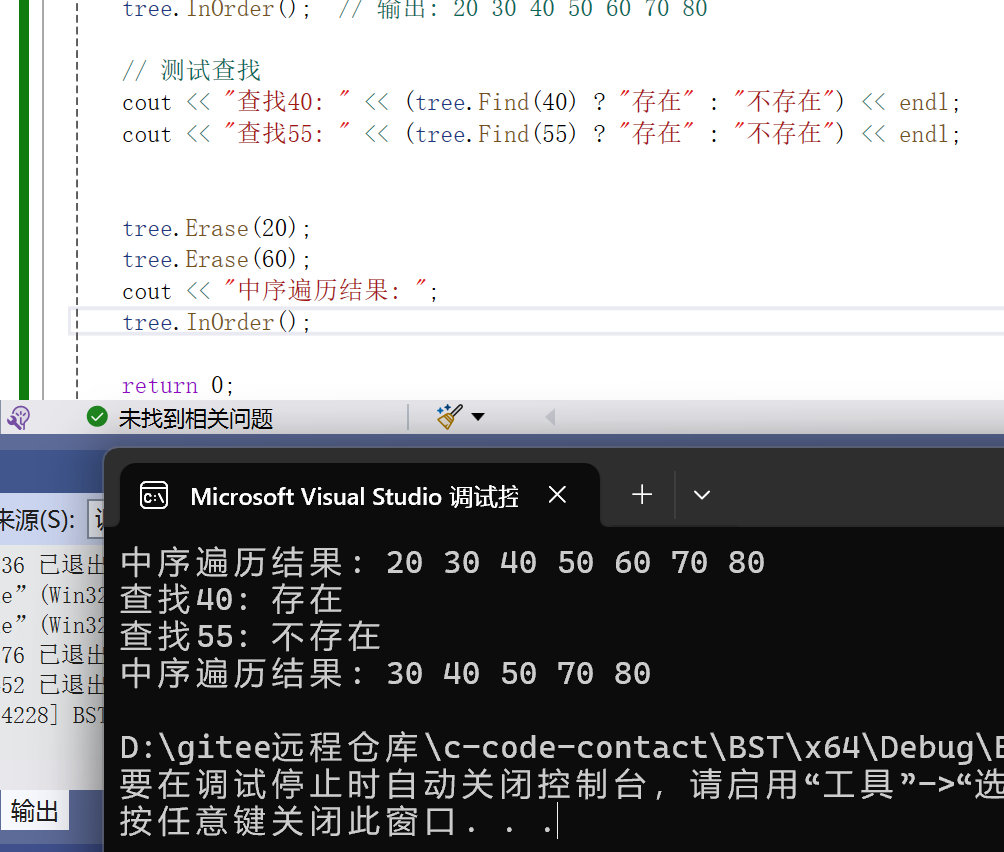
三、二叉树的应用

K模型

K模型：K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到
的值。

比如：给一个单词word，判断该单词是否拼写正确，具体方式如下：
以词库中所有单词集合中的每个单词作为key，构建一棵二叉搜索树
在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误。

KV模型

KV模型：每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。该种方
式在现实生活中非常常见：

比如英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英 文单词与其对应的中文就构成一种键值对；

再比如统计单词次数，统计成功后，给定单词就可快速找到其出现的次数，单词与其出 现次数就是就构成一种键值对。

KV代码实现

cpp 复制代码 
#include <iostream>
#include <string>
using namespace std;

template<class K, class V>
struct BSTNode {
    BSTNode(const K& key = K(), const V& value = V())
        : _pLeft(nullptr), _pRight(nullptr), _key(key), _value(value) {}

    BSTNode<K, V>* _pLeft;
    BSTNode<K, V>* _pRight;
    K _key;
    V _value;
};

template<class K, class V>
class BSTree {
    typedef BSTNode<K, V> Node;
    typedef Node* PNode;
public:
    BSTree() : _pRoot(nullptr) {}

    // 查找节点（非递归）
    PNode Find(const K& key) {
        PNode cur = _pRoot;
        while (cur) {
            if (key < cur->_key) {
                cur = cur->_pLeft;
            }
            else if (key > cur->_key) {
                cur = cur->_pRight;
            }
            else {
                return cur;
            }
        }
        return nullptr;
    }

    // 插入节点（非递归）
    bool Insert(const K& key, const V& value) {
        if (_pRoot == nullptr) {
            _pRoot = new Node(key, value);
            return true;
        }

        PNode parent = nullptr;
        PNode cur = _pRoot;
        while (cur) {
            parent = cur;
            if (key < cur->_key) {
                cur = cur->_pLeft;
            }
            else if (key > cur->_key) {
                cur = cur->_pRight;
            }
            else {
                return false; // 键已存在
            }
        }

        if (key < parent->_key) {
            parent->_pLeft = new Node(key, value);
        }
        else {
            parent->_pRight = new Node(key, value);
        }
        return true;
    }

    // 删除节点（非递归）
    bool Erase(const K& key) {
        PNode parent = nullptr;
        PNode cur = _pRoot;
        
        // 查找要删除的节点及其父节点
        while (cur && cur->_key != key) {
            parent = cur;
            if (key < cur->_key) {
                cur = cur->_pLeft;
            }
            else {
                cur = cur->_pRight;
            }
        }
        
        if (cur == nullptr) return false; // 未找到要删除的节点

        // 情况1：删除的节点有两个子节点
        if (cur->_pLeft && cur->_pRight) {
            PNode minRight = cur->_pRight;
            PNode minRightParent = cur;
            
            // 找到右子树中的最小节点
            while (minRight->_pLeft) {
                minRightParent = minRight;
                minRight = minRight->_pLeft;
            }
            
            // 用最小节点的值替换当前节点值
            cur->_key = minRight->_key;
            cur->_value = minRight->_value;
            
            // 转换为删除minRight（此时minRight最多有一个右子节点）
            cur = minRight;
            parent = minRightParent;
        }

        // 情况2和3：删除的节点有0或1个子节点
        PNode child = cur->_pLeft ? cur->_pLeft : cur->_pRight;
        
        if (parent == nullptr) { // 删除的是根节点
            _pRoot = child;
        }
        else if (parent->_pLeft == cur) {
            parent->_pLeft = child;
        }
        else {
            parent->_pRight = child;
        }
        
        delete cur;
        return true;
    }

    // 中序遍历（递归）
    void InOrder() {
        _InOrder(_pRoot);
        cout << endl;
    }

private:
    PNode _pRoot;

    void _InOrder(PNode node) {
        if (node) {
            _InOrder(node->_pLeft);
            cout << node->_key << ":" << node->_value << " ";
            _InOrder(node->_pRight);
        }
    }
};

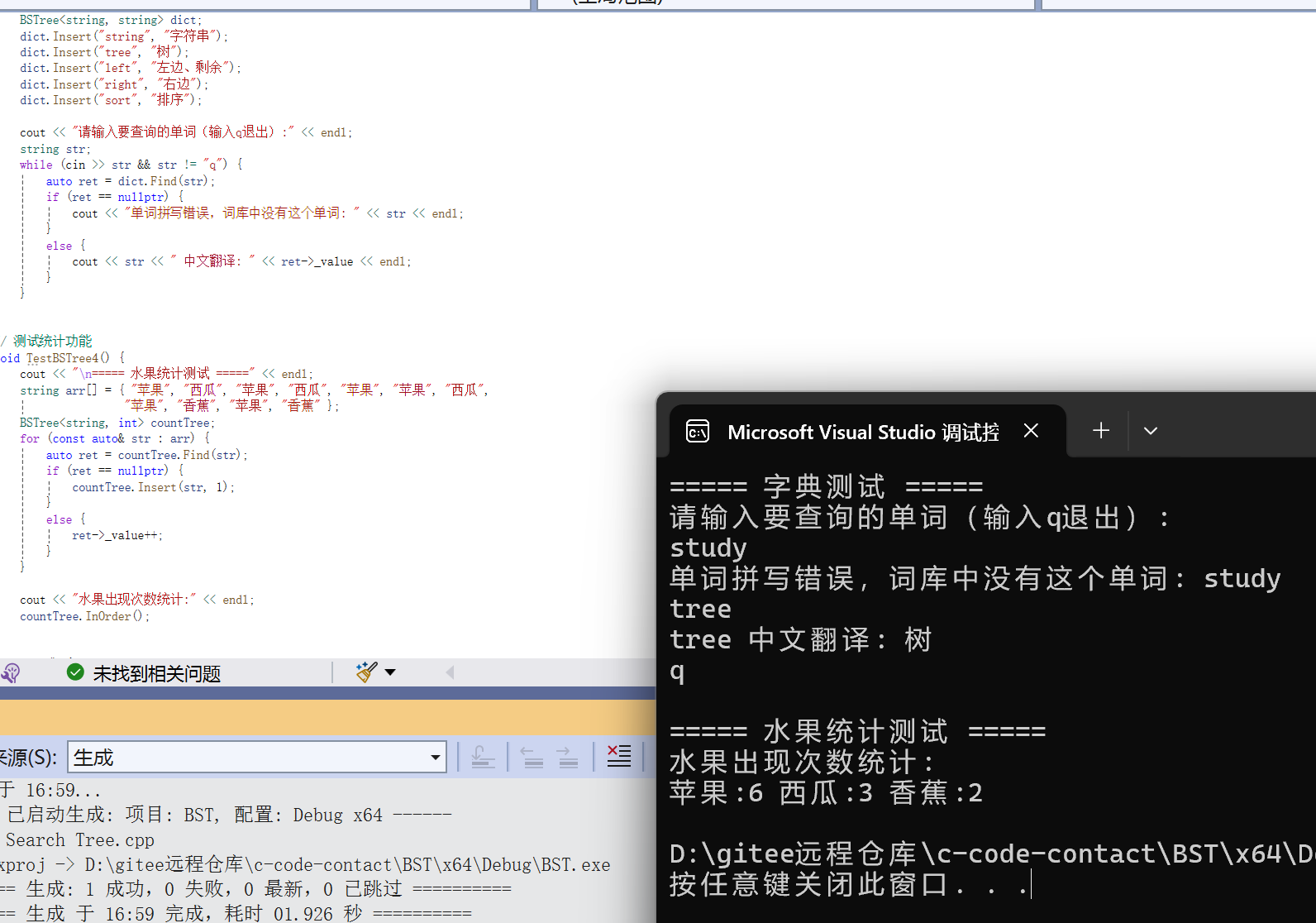
// 测试字典功能
void TestBSTree3() {
    cout << "===== 字典测试 =====" << endl;
    BSTree<string, string> dict;
    dict.Insert("string", "字符串");
    dict.Insert("tree", "树");
    dict.Insert("left", "左边、剩余");
    dict.Insert("right", "右边");
    dict.Insert("sort", "排序");

    cout << "请输入要查询的单词（输入q退出）:" << endl;
    string str;
    while (cin >> str && str != "q") {
        auto ret = dict.Find(str);
        if (ret == nullptr) {
            cout << "单词拼写错误，词库中没有这个单词: " << str << endl;
        }
        else {
            cout << str << " 中文翻译: " << ret->_value << endl;
        }
    }
}

// 测试统计功能
void TestBSTree4() {
    cout << "\n===== 水果统计测试 =====" << endl;
    string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜",
                    "苹果", "香蕉", "苹果", "香蕉" };
    BSTree<string, int> countTree;
    for (const auto& str : arr) {
        auto ret = countTree.Find(str);
        if (ret == nullptr) {
            countTree.Insert(str, 1);
        }
        else {
            ret->_value++;
        }
    }

    cout << "水果出现次数统计:" << endl;
    countTree.InOrder();
}

int main() {
    TestBSTree3();
    TestBSTree4();
    return 0;
}
相关推荐
杂亿稿2 小时前
优先级队列
数据结构
小old弟2 小时前
后端三层架构
java·后端
金融街小单纯2 小时前
随机刺激训练：解锁跨学科洞察力的科学密码
算法·重构·区块链
花花鱼2 小时前
spring boot 2.x 与 spring boot 3.x 及对应Tomcat、Jetty、Undertow版本的选择（理论）
java·后端
要争气3 小时前
5 二分查找算法应用
java·数据结构·算法
欧阳x天3 小时前
堆(超详解)
数据结构
空荡forevere3 小时前
《操作系统真象还原》 第十章 输入输出系统
开发语言·c++·操作系统
小咕聊编程3 小时前
【含文档+PPT+源码】基于springboot的旅游路线推荐系统的设计与实现
spring boot·后端·旅游
道可到3 小时前
阿里面试原题 java面试直接过06 | 集合底层——HashMap、ConcurrentHashMap、CopyOnWriteArrayList
java·后端·面试
热门推荐
01BongoCat - 跨平台键盘猫动画工具02智能库存管理的需求预测模型：从业务痛点到落地代码的完整实践03两千字总结：Codex 国内如何安装和使用的教程，以及如何设置中文回答042025羊城杯网络安全大赛 wp05GitHub 镜像站点06UV安装并设置国内源07Linux下V2Ray安装配置指南085大DOM/BOM核心考点：从入门到精通，让面试官眼前一亮09Spring Boot 实现微信登录，So Easy !10Cursor Plan Mode：AI 终于知道先想后做了