b树，b+树，红黑树

一、B树

视频

1.特点

平衡，有序，多路

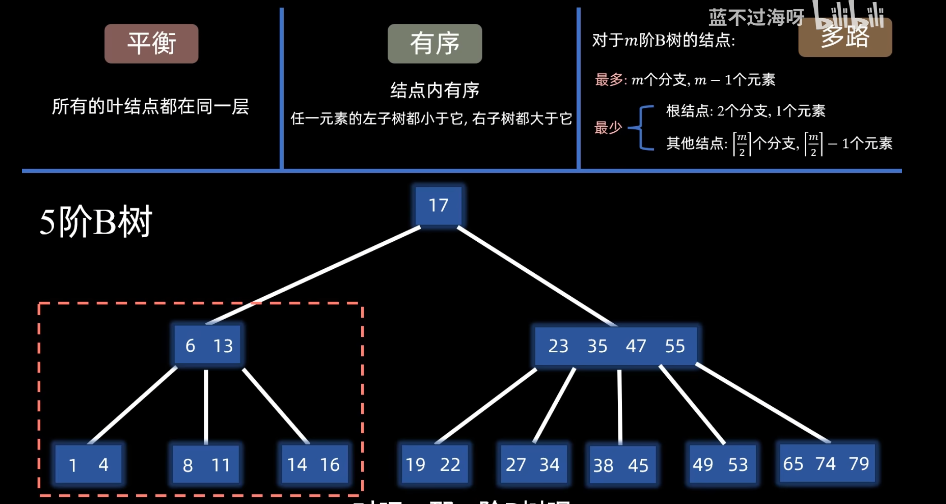
2. 查找

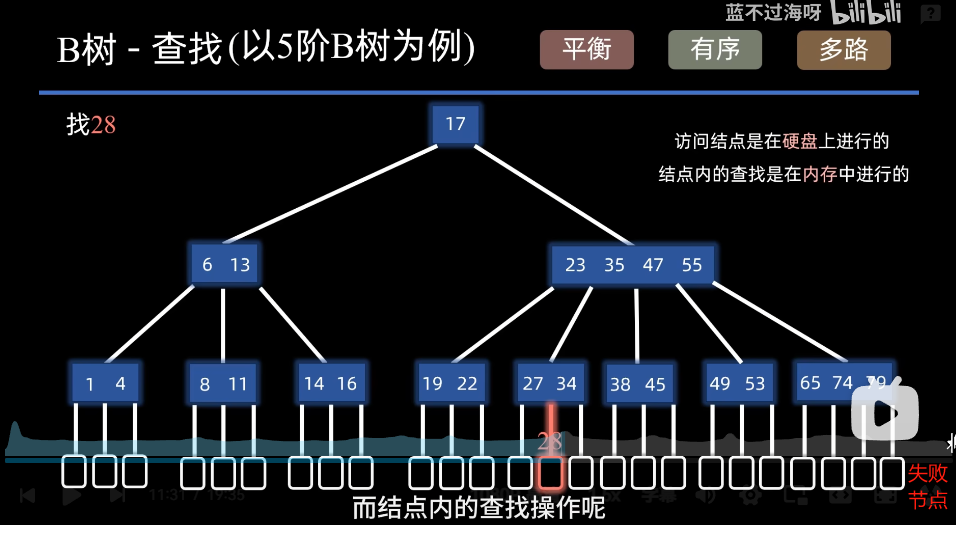
访问节点在硬盘上进行，节点内查找在内存上进行，树高就是读取硬盘的次数。

每个节点里的数据是有序的（查找时可以顺序查找或者二分查找）

3. 插入

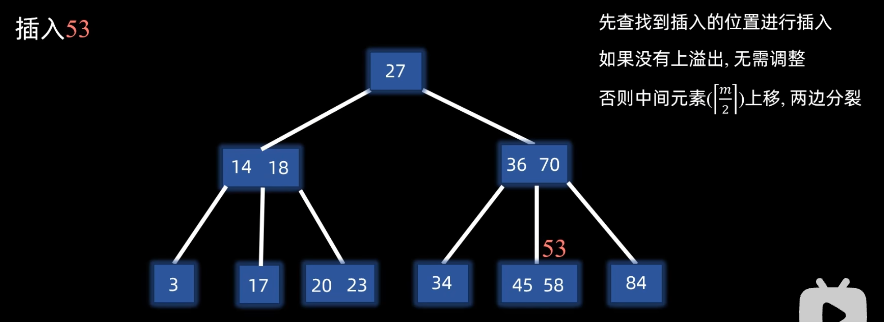
先查找到插入的位置进行插入，如果没有上溢出，无需调整

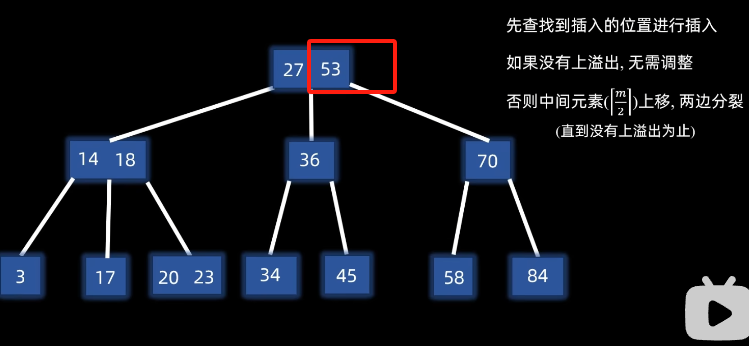
如果有，则否则中间元素 ⌈ m 2 ⌉ \left\lceil \frac{m}{2} \right\rceil ⌈2m⌉上移，左右两边分裂

（直到没有上溢出为止)

• 插入，无上溢出：
  例子插入20：

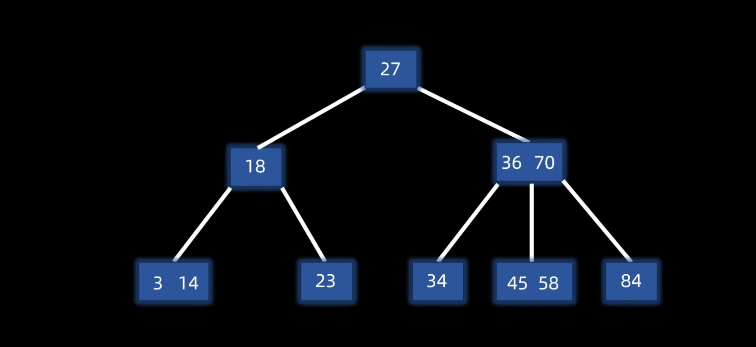
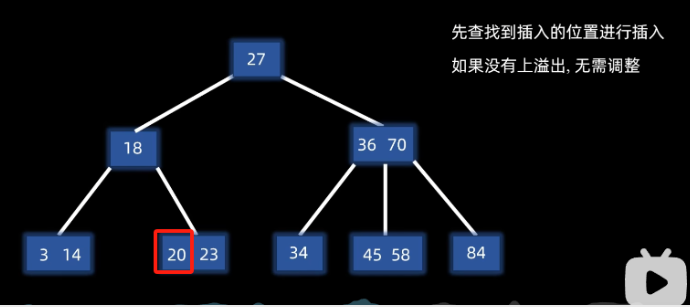
• 有上溢出则中间节点上移到父亲节点，两边节点往两边分裂：
  例子插入53：
  
  

4. 构建

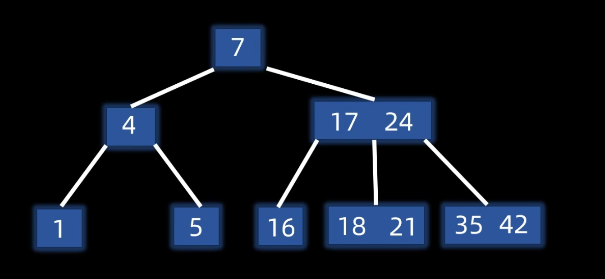
1，5，7，4，16，35，24，42，21，17 ，18构造的B树如下：

5. 删除

删除时可能出现下溢出，即节点内数据少于最小个数 ⌈ m 2 ⌉ − 1 \left\lceil \frac{m}{2} \right\rceil-1 ⌈2m⌉−1

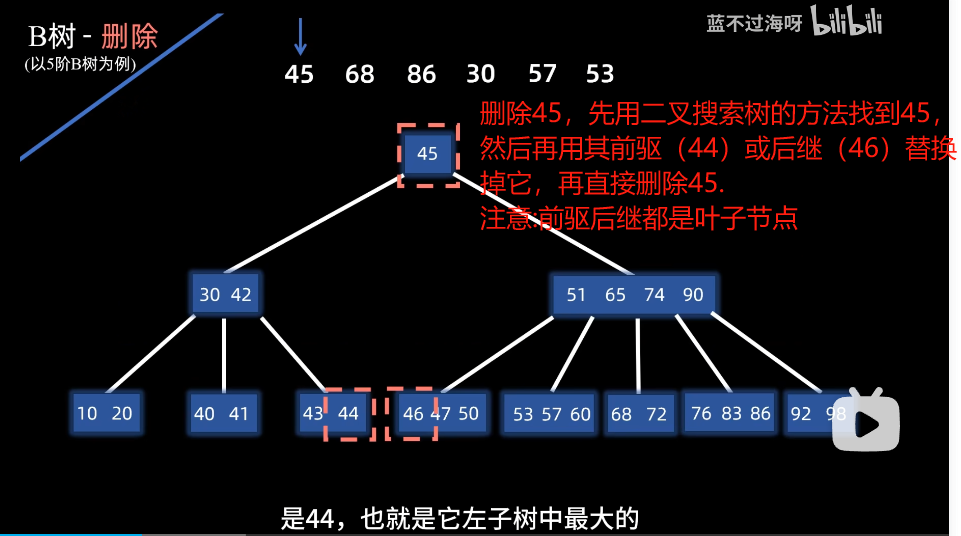
• 删除非叶子节点

  例子：删除45
  
  
  

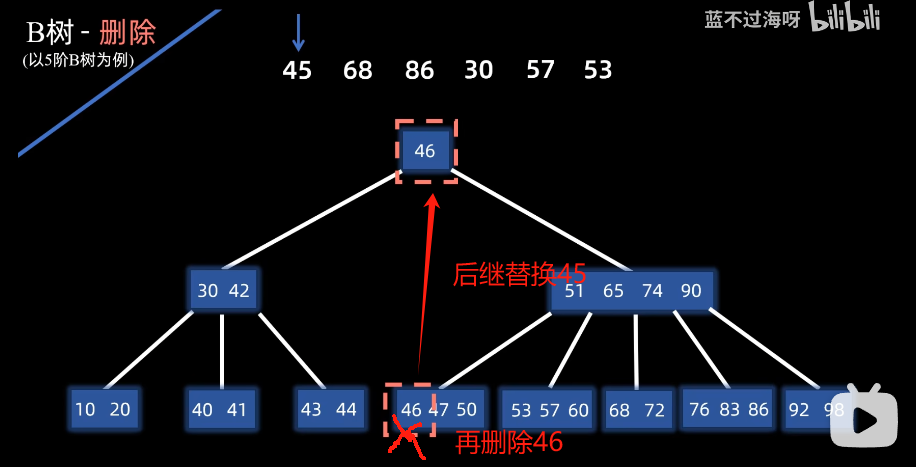
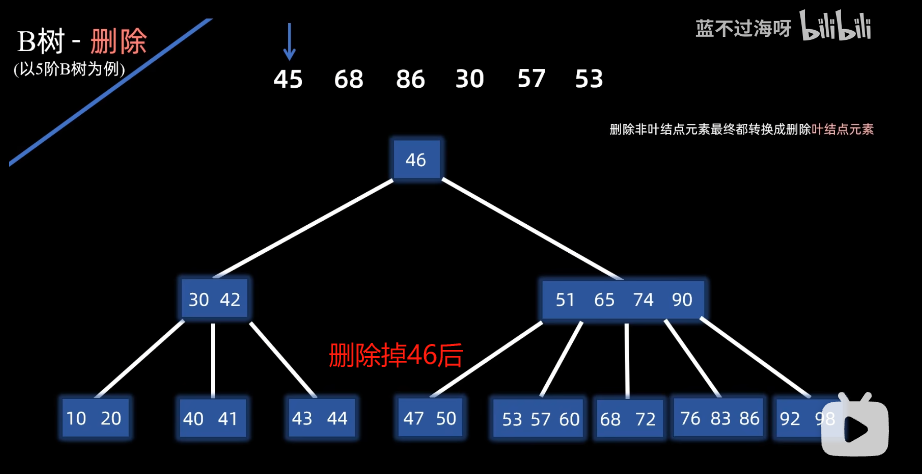
• 叶子节点：直接删除

• 删除非叶子节点出现下溢出

  例子：删除68后下溢出，则看兄弟是否够够借

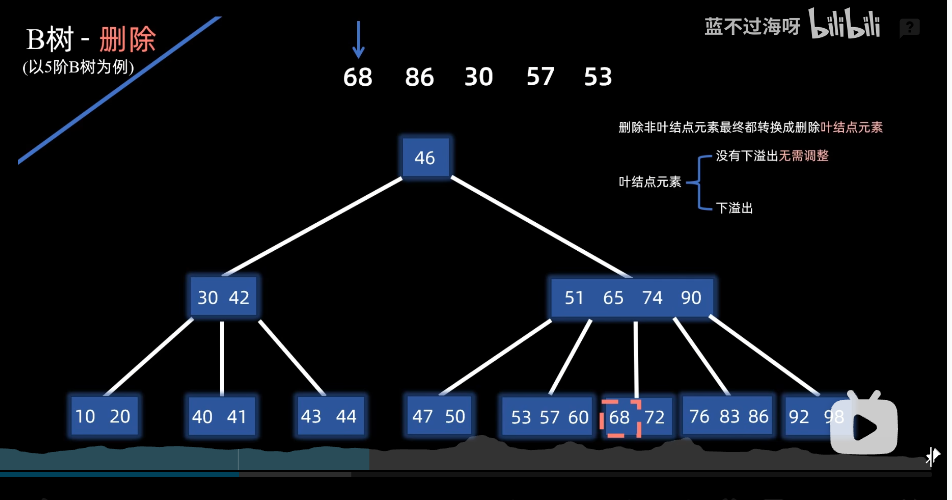
  假如借左兄弟的，则父下来，兄上去

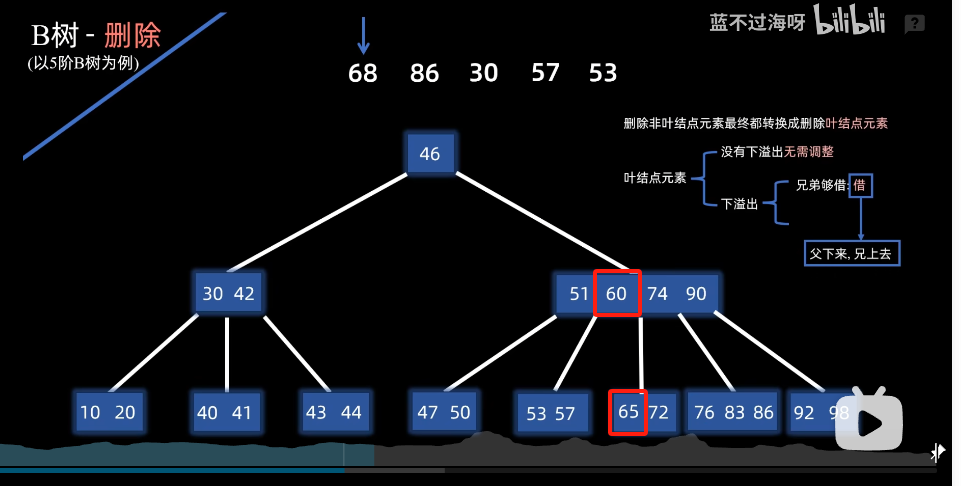
• 如果删除后，兄弟不够借的情况：

  例子：删除86，只剩下83了，左右两边不够借
  

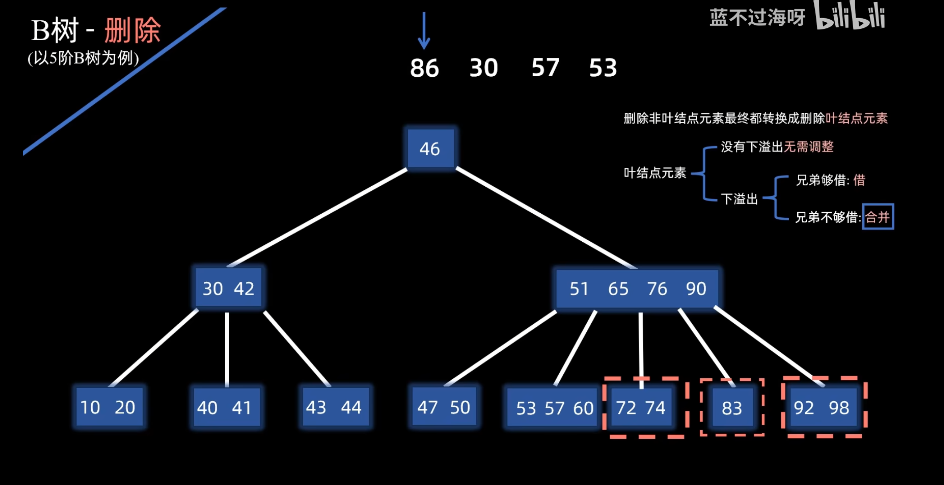
合并，父下移左，然后右并过来 ，结果如下：

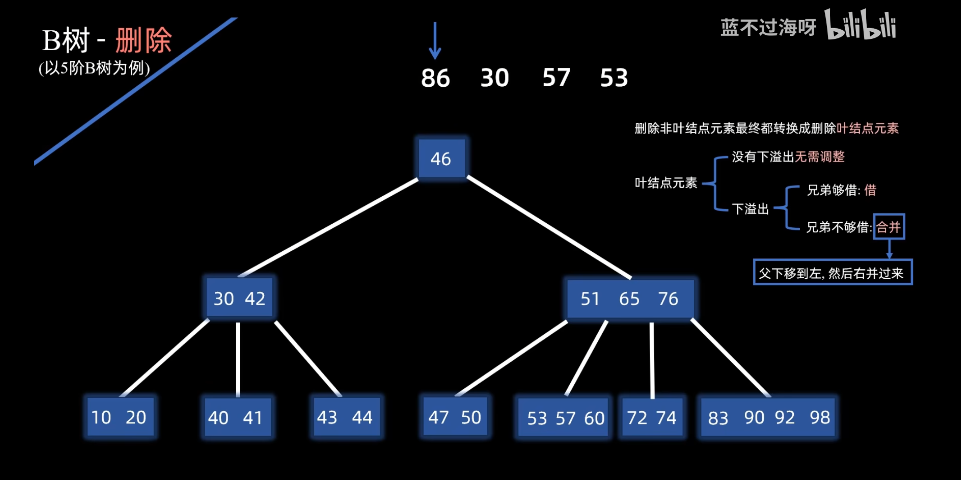
二、B+树

视频

1.特点：

1. m个分支m个元素
2. 非叶子节点对应孩子节点的对大值，存储的都是叶子节点的关键字，相当于是索引的索引，所以是多级索引结构
   

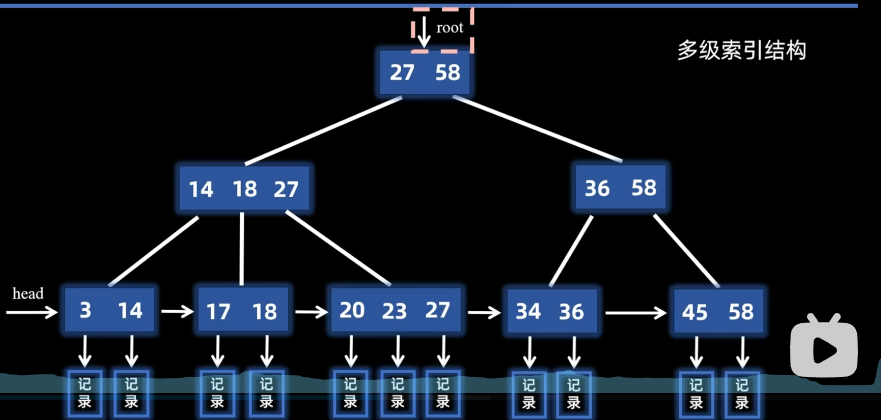
2. B+树的叶子节点：

• 叶子包含了所有元素

• 叶子从小到大排列，节点之间通过指针链接成链表结构，可以通过头指针快速对节点顺序遍历，不用像B树那样通过中序顺序遍历

• B+树常用作数据库的索引

  • InnoDB 引擎（聚簇索引 为主）：叶子节点存储的是直接存储整行数据，即该索引键对应的完整记录。二级索引（如普通索引、唯一索引）的叶子节点：不存整行数据，只存储对应的主键值，查询时需通过主键值回表（到聚簇索引）获取完整数据。
  • MyISAM 引擎（非聚簇索引 ）
    无论主键索引还是二级索引，叶子节点都不存整行数据，只存储数据在物理文件中的地址（偏移量） ，查询时需通过地址去数据文件中读取完整记录

叶子内的元素叫作关键字

数据库中的某个记录 （就是表中的每一行）。

b+树和数据库表都存在硬盘
MySQL中：
存储介质 ：表结构和索引的 B + 树均持久化在磁盘中（以文件形式存在），是数据长期存储的基础。
操作方式：通过索引查询时，会先将 B + 树的相关节点（页）从磁盘加载到内存（缓冲池），再在内存中通过关键字遍历（如二分法）快速定位目标，最终获取数据。这一过程通过 "内存中高效处理 + 减少磁盘 IO" 实现了索引的快速查询。

3. 解释MyISAM中的索引（非聚簇索引）

MyISAM 引擎的索引与 InnoDB 有本质区别：数据和索引完全分离存储 （数据存在.MYD文件，索引存在.MYI文件），且无论主键索引还是二级索引，叶子节点都只存储数据在物理文件中的地址 （偏移量），而非完整数据或主键值。
特点：

• 所有索引（主键索引、二级索引）都是 "非聚簇索引"，索引与数据分开存储；
• 索引的叶子节点不存数据本身，只存数据记录在.MYD文件中的物理地址（类似指针，指向数据的具体位置）；
• 主键索引和二级索引的结构逻辑一致，区别仅在于 "索引关键字" 不同（主键字段 vs 二级索引字段）。
  如下图：
  
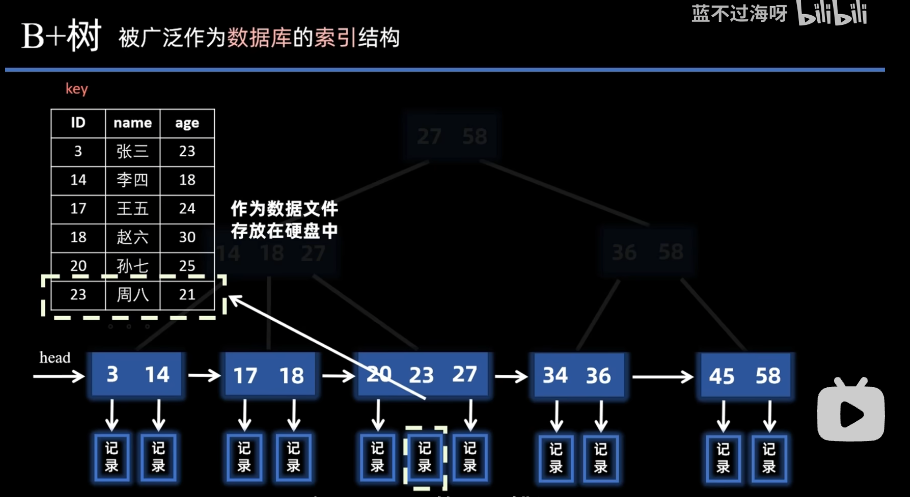
  举例子解释：
  
  
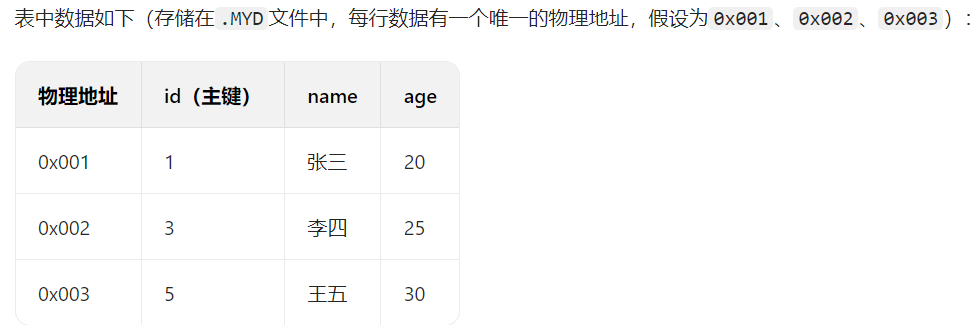
  二级索引与主键索引的查找逻辑一摸一样，只是存储的是二级索引的关键字和地址
  

4. 解释InnoDB中的索引（MySQL）：

5. MyISAM和InnoDB的索引区别

6. 查找

B+树的查找最终都落在叶子节点上，因为只有叶子节点存储的才是记录。

1. 顺序查找：直接顺序遍历叶子的链表
2. 随机查找：通过root指针逐层对比大小向下查找，对比过程是先和节点内的第一个比较（最小值），比它大则在节点内继续比较，比它小则往下面的左子树比较，log级别的复杂度
3. 范围查找
   比如查找1-0~50，先找最小值10，发现不存在，最小值就是14，然后从14开始顺序遍历链表，直到找到45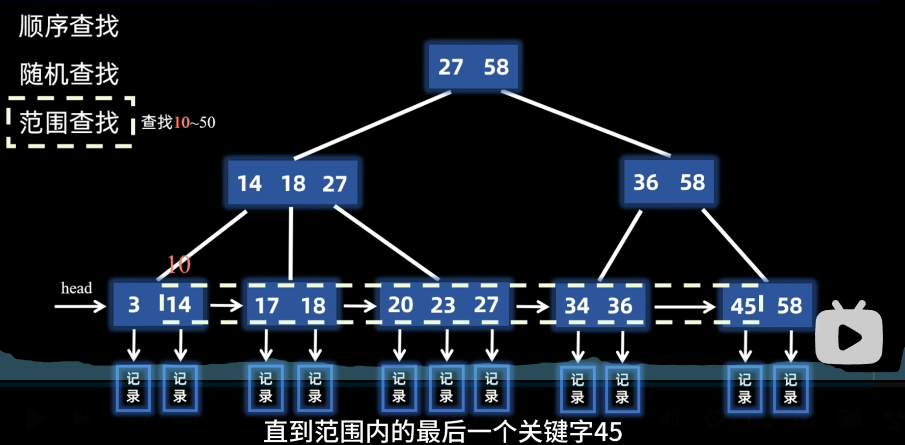

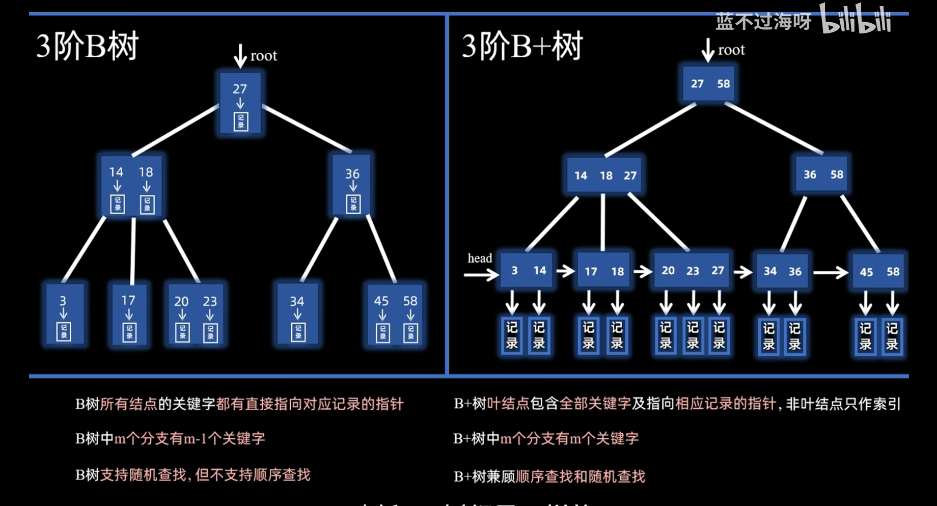
三、B树和B+树的对比

四、红黑树

视频

红黑树是一个二叉搜索树，它和AVL树一样，都是对二叉搜索树进行了平衡，只是平衡的策略不同。

1. 特点

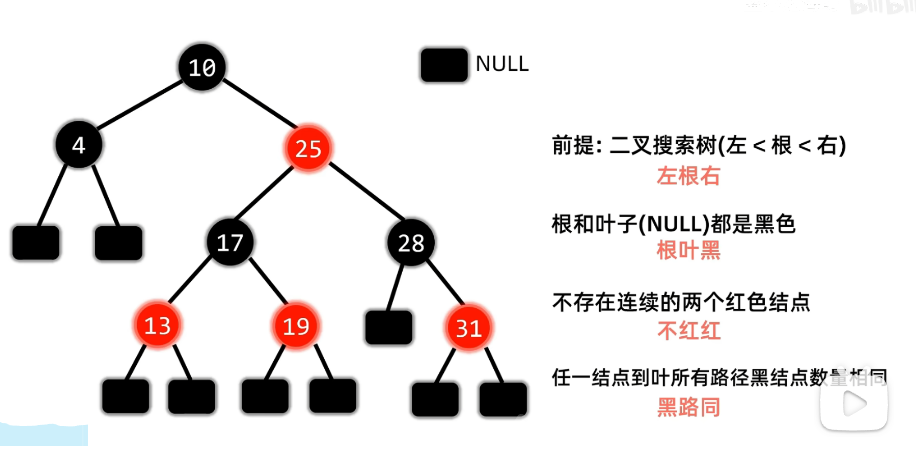
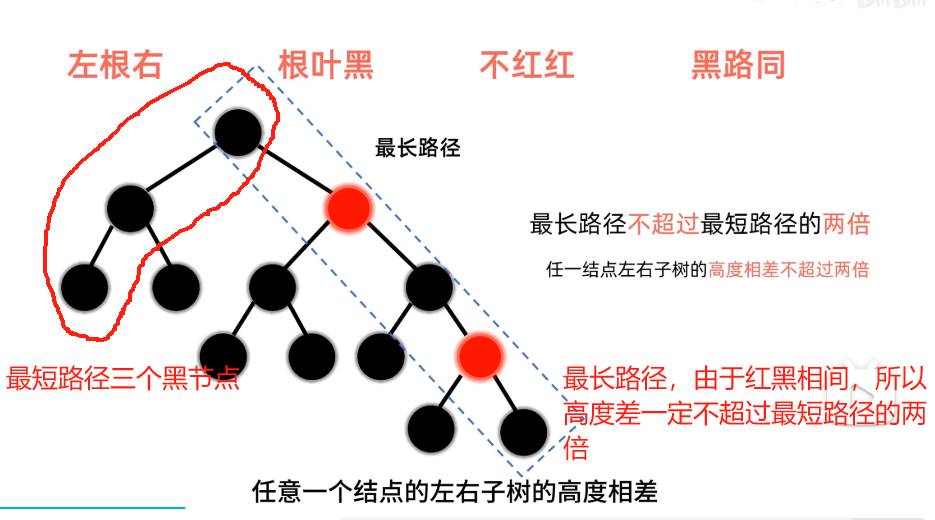
2. 插入

插入规则：

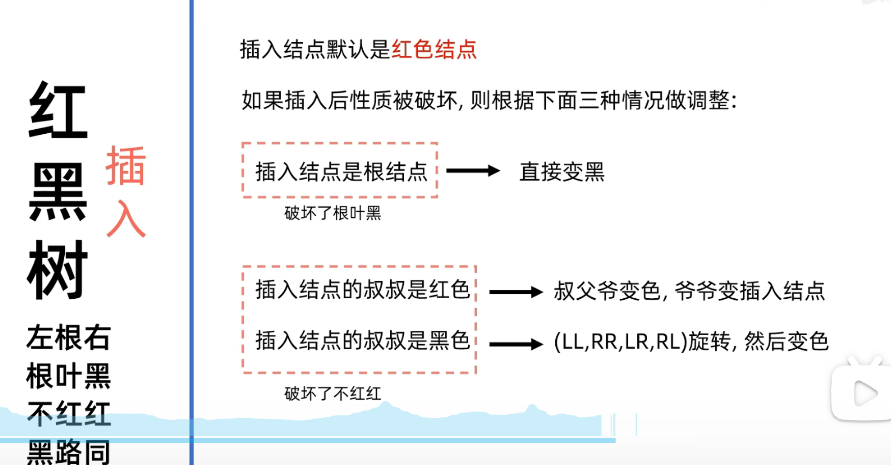
例子：插入节点叔叔是红色

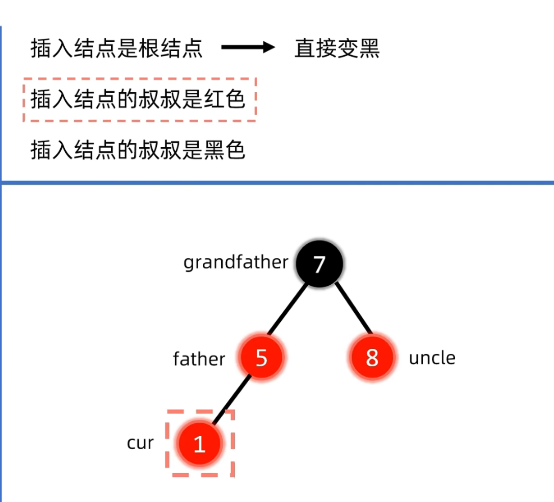
插入后：

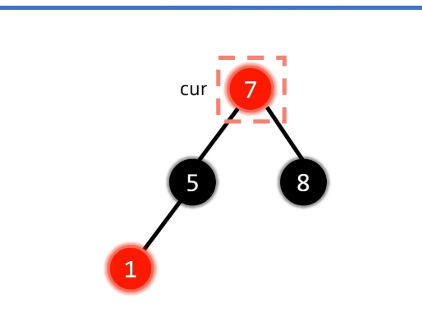
例子2：插入节点叔叔是黑色

插入前：

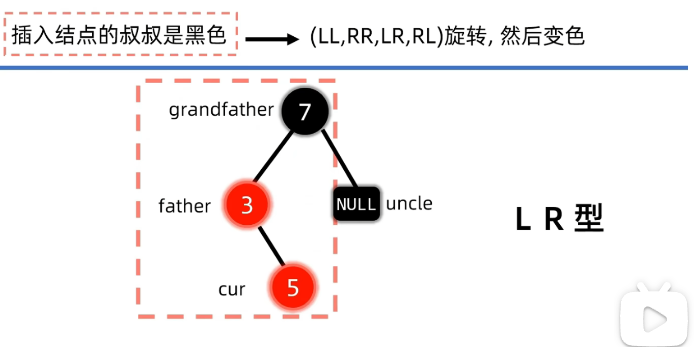
插入后：

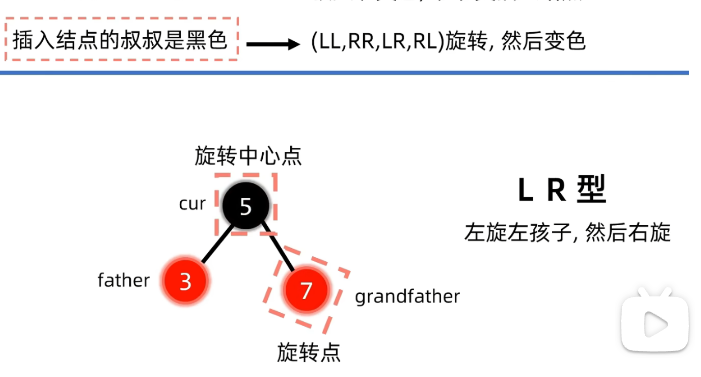
构建例子：

注意：插入顺序不同，构造的红黑树通常不一样

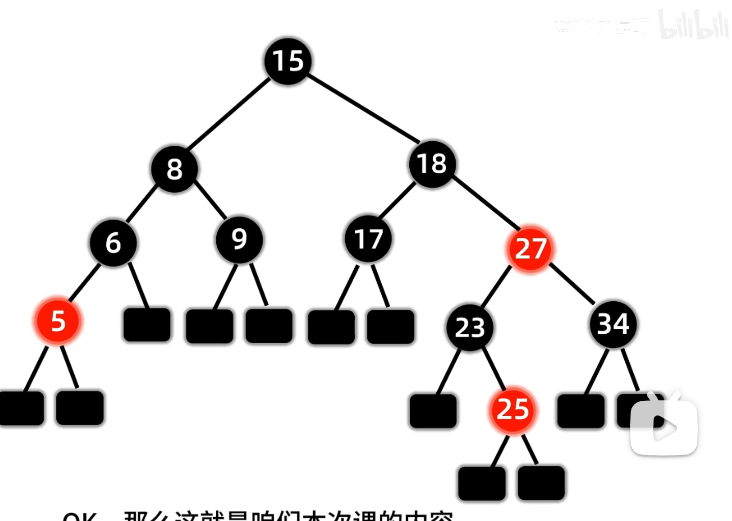
3. 与AVL树对比

**查询：**时间复杂度都是O（logN），红黑树小于AVL树（因为AVL树高度差不超过1，红黑树不超过两倍，即AVL树平衡要求更严格，所以红黑树查询效率更慢）
插入删除：红黑树更好（因为AVL平衡性更严格，所以旋转次数更多）

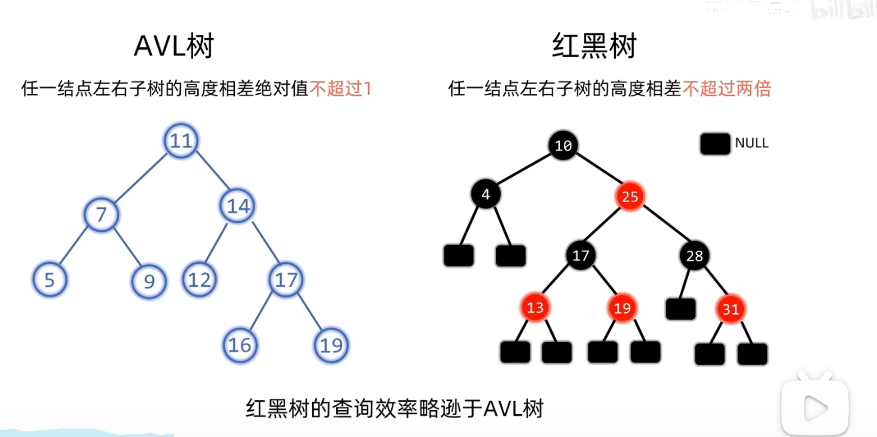
红黑树和AVL树都是自平衡二叉搜索树（即满足"左子树值≤根节点值≤右子树值"的特性，同时通过旋转维持平衡），但两者的平衡策略和适用场景有显著差异。以下先明确红黑树的核心特性，再从多个维度对比两者的区别。

对比维度	红黑树	AVL树
平衡策略	通过"颜色规则+黑高一致"维持近似平衡（最长路径≤最短路径×2）	通过"平衡因子"维持严格平衡（左右子树高度差≤1）
旋转操作频率	插入最多需2次旋转，删除最多需3次旋转（旋转少）	插入/删除可能需要多次旋转（因需严格维持高度差）
空间开销	只需存储一个"颜色"标记（额外空间少）	需要存储"平衡因子"或"高度"（额外空间更多）
查找效率	略低（树高略大，最坏O(log n)，但常数因子小）	更高（树高更矮，严格平衡，最坏O(log n)）
插入/删除效率	更高（旋转少，维护成本低）	更低（旋转频繁，维护成本高）
适用场景	插入/删除频繁的场景，如Java中HashMap，TreeMap，TreeSet	查询操作远多于插入/删除的场景（如静态数据索引）