二分算法是我觉得在基础算法篇章中最难的算法。二分算法的原理以及模板其实是很简单的,主要的难点在于问题中的各种各样的细节问题。因此,大多数情况下,只是背会二分模板并不能解决题目,还要去处理各种乱七八糟的边界问题。
一、二分查找
【算法原理】
当我们的解具有二段性时,就可以使用二分算法找出答案:
根据待查找区间的中点位置,分析答案会出现在哪一侧;
接下来舍弃一半的待查找区间,转而在有答案的区间内继续使用二分算法查找结果。
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]示例 3:
输入:nums = [], target = 0
输出:[-1,-1]提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109nums是一个非递减数组-109 <= target <= 109
【解法一】暴力解法->从前往后扫描数组
慢就慢在没有利用数组有序的特性,O(N)
【解法二】二分算法
契机:发现解集中,存在二段性
1.查找起始位置
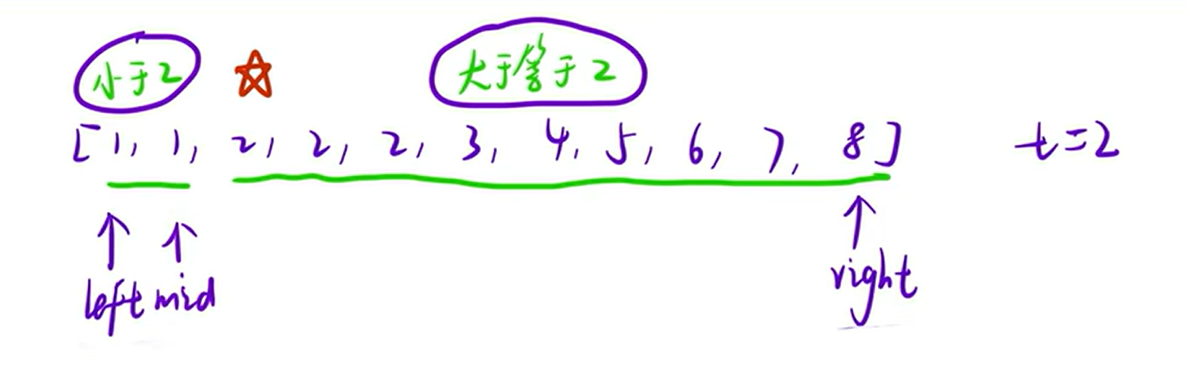 细节问题:
细节问题:
1)while循环里面的判断如何写?
while ( left < right ) √
while ( left < right ) × 死循环

一直命中第一个条件,left=right=0后,一直死循环
2)求中点的方式?
( left + right ) / 2 ; √
( left + right + 1) / 2 ; ×
3)二分结束之后,相遇点的情况
2.查找终止位置
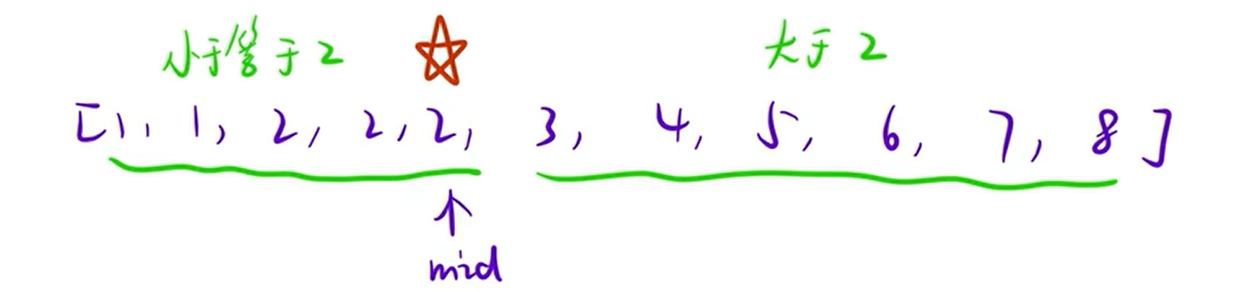
1)while循环里面的判断如何写?
while ( left < right ) √
while ( left < right ) × 死循环
2)求中点的方式?
( left + right ) / 2 ; × 死循环
( left + right + 1) / 2 ; √
【模板】
cpp
//查找区间左端点
int l = 1, r = n;
while (l < r)
{
int mid = (l + r) / 2;
if (check(mid))
r = mid;
else
l = mid + 1;
}
//二分结束之后可能需要判断是否存在结果
cpp
//查找区间右端点
int l = 1;r = n;
while (l < r)
{
int mid = (l + r + 1) / 2;
if (check(mid))
l = mid;
else
r = mid - 1;
}
//二分结束之后可能需要判断是否存在结果【注】为防止溢出,求中点时:
mid = l + ( r - l ) / 2 ;
【时间复杂度】
每次二分都会砍掉一半的查找区域,O(logN)
cpp
class Solution
{
public:
vector<int> searchRange(vector<int>& nums, int target)
{
int n=nums.size();
if(n==0)
return {-1,-1};
if(nums[0]>target)
return {-1,-1};
if(nums[n-1]<target)
return {-1,-1};
int l=0;
int r=n-1;
int m=(l+r)/2;
//查找起始位置
while(l<r)
{
m=(l+r)/2;
if(nums[m]>=target)
r=m;
else
l=m+1;
}
//l或r所指的位置有可能是最终答案
if(nums[l]!=target)
return {-1,-1};
int retleft=l;
l=0,r=n-1;
//查找终止位置
while(l<r)
{
m=(l+r+1)/2;
if(nums[m]<=target)
l=m;
else
r=m-1;
}
return {retleft,l};
}
};【二分问题解决流程】
1.先画图分析,确定使用左端点模板还是右端点模板,还是两者配合一起使用;
2,二分出结果之后,不要忘记判断结果是否存在,二分问题细节众多,一定要分析全面。
【STL中的二分查找】
<algorithm>
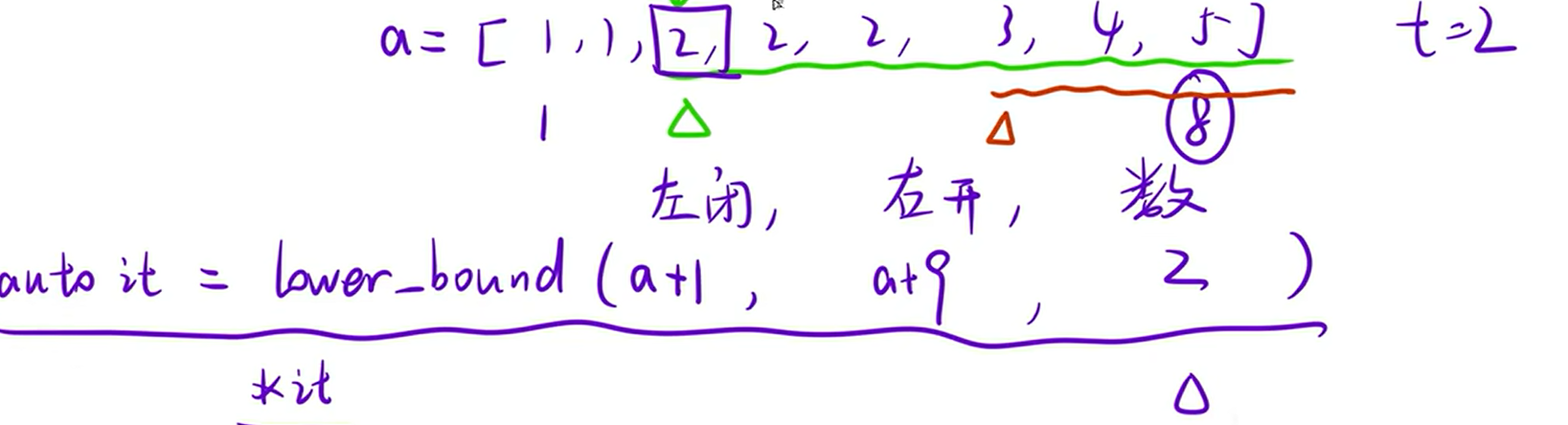
1.lower_bound:大于等于x的最小元素,返回的是迭代器;时间复杂度:O(logN)。
2.upper_bound:大于x的最小元素,返回的是迭代器。时间复杂度:O(logN)。
二者均采用二分实现。但是STL中的二分查找只能适用于"在有序的数组中查找",如果是二分答案就不能使用。因此还是需要记忆二分模板。
二、二分答案
题目描述
木材厂有 n 根原木,现在想把这些木头切割成 k 段长度均为 l 的小段木头(木头有可能有剩余)。
当然,我们希望得到的小段木头越长越好,请求出 l 的最大值。
木头长度的单位是 cm,原木的长度都是正整数,我们要求切割得到的小段木头的长度也是正整数。
例如有两根原木长度分别为 11 和 21,要求切割成等长的 6 段,很明显能切割出来的小段木头长度最长为 5。
输入格式
第一行是两个正整数 n,k,分别表示原木的数量,需要得到的小段的数量。
接下来 n 行,每行一个正整数 Li,表示一根原木的长度。
输出格式
仅一行,即 l 的最大值。
如果连 1cm 长的小段都切不出来,输出 0。
输入输出样例
输入 #1复制
3 7
232
124
456输出 #1复制
114说明/提示
数据规模与约定
对于 100% 的数据,有 1≤n≤105,1≤k≤108,1≤Li≤108(i∈[1,n])。
准确来说,应该叫做「二分答案+判断」。
二分答案可以处理大部分「最大值最小」以及「最小值最大」的问题。如果「解空间」在从小到大的「变化」过程中,「判断」答案的结果出现「二段性」,此时我们就可以「二分」这个「解空间」,通过「判断」,找出最优解。
刚接触的时候,可能觉得这个「算法原理」很抽象。没关系,练习过后,你会发现这个「二分答案」的原理其实很容易理解,重点是如何去「判断」答案的可行性。
x表示:切割出来的小段的长度
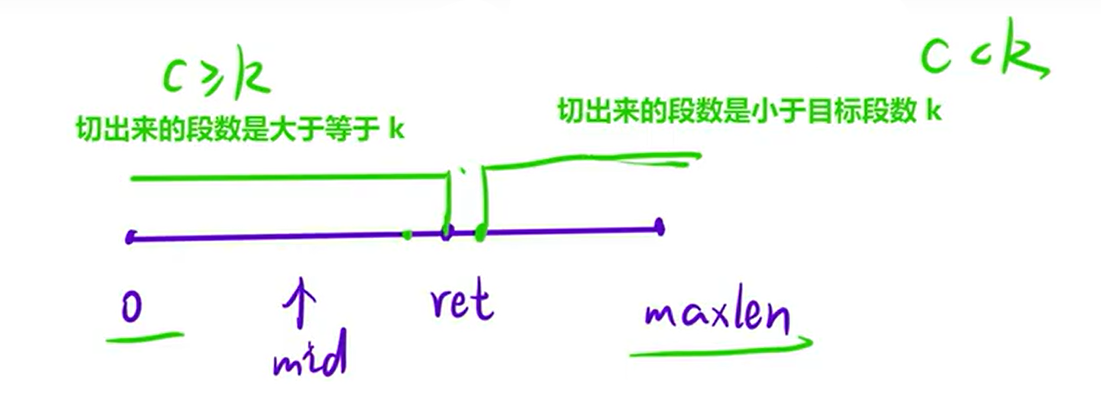
c表示:在x的基础下,最多能切出来多少段
k表示:最终要切割的段数
解法一:暴力解法
枚举所有的切割长度x
求出在x的情况下,能够切出来多少段
解法二:利用二分来优化
x增大,c减小。x减小,c增大。
二段性
Calc(x)
计算切割长度为x的时候,能切出来多少段