反转链表及其应用（力扣2130）

题目一：206. 反转链表 - 力扣（LeetCode）

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

复制代码

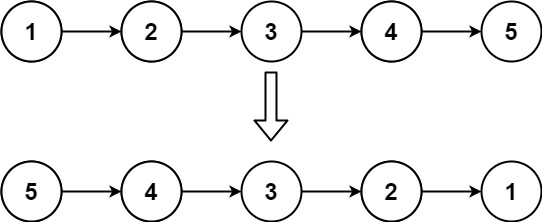
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

示例 2：

复制代码

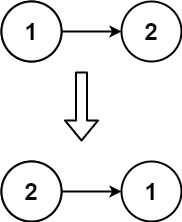
输入：head = [1,2]
输出：[2,1]

示例 3：

复制代码

输入：head = []
输出：[]

提示：

链表中节点的数目范围是 [0, 5000]
-5000 <= Node.val <= 5000

**进阶：**链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题？

方法一：迭代

从头开始，两两一组，调整指针的指向即可。对于A->B->C来说，调整为A<-B->C后，需要记录C，不然就不知道哪个节点要指向B了。此外，为了避免第一个节点与第二个节点互相指向，第一个位置应该为空节点，第二个位置应该才是第一个节点。

cpp 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode*prev=nullptr;
        ListNode*curr=head;
        while(curr) {
            ListNode*tmp=curr->next;
            curr->next=prev;
            prev=cur;
            curr=tmp;
        }
        return prev;
    }
};

方法二：递归

对于链表A->B->C->D来说，想要反转A->B，不妨先反转B->C；想要反转B->C，不妨先反转C->D；这是"递"。发现D后面没了，正式开始反转，然后再一个个出栈，这是"归"。

cpp 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */ 
class Solution {
public:
    ListNode* func(ListNode*prev,ListNode*curr) {
        //确定终止条件，归
        if(curr==nullptr) return prev;

        //处理单层逻辑
        ListNode*tmp=curr->next;
        curr->next=prev;

        //递
        return func(curr,tmp);
    }
    ListNode* reverseList(ListNode* head) {
        return func(nullptr,head);//依然要避免头两个节点互相指向
    }
};

之所以直接返回func(nullptr,head)，是因为每一个对子（prev,curr）的函数都返回的是下一个对子（curr,tmp）的函数的返回值，也就是说，func(A,B)返回值依赖func(B,C)，func(B,C)返回值依赖func(C,D)，最终的返回值就是func(D,nullptr)，也就是新链表的头节点。

题目二：92. 反转链表 II - 力扣（LeetCode）

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。

示例 1：

复制代码

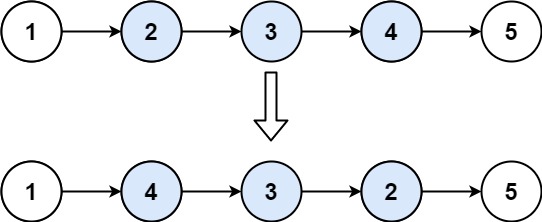
输入：head = [1,2,3,4,5], left = 2, right = 4
输出：[1,4,3,2,5]

示例 2：

复制代码

输入：head = [5], left = 1, right = 1
输出：[5]

提示：

链表中节点数目为 n
1 <= n <= 500
-500 <= Node.val <= 500
1 <= left <= right <= n

进阶： 你可以使用一趟扫描完成反转吗？

这题不一样的地方在于，它只要求我们反转链表中的一部分。大同小异，其实第一题也可以理解成反转链表中的一部分，只不过头尾都是nullptr罢了。

首先，我们要先给一个虚拟头节点dummy_head，因为有可能第一个节点因为反转去到了其它地方。

方法一：

找到待反转部分最左侧节点的前一个节点和最右侧节点的后一个节点，再把待反转部分单独抽出来，回到上一个问题，再调整指针指向即可。

cpp 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    void reverse(ListNode*head) {
        ListNode*pre=nullptr;
        ListNode*cur=head;
        while(cur) {
            ListNode*tmp=cur->next;
            cur->next=pre;
            pre=cur;
            cur=tmp;
        }
    }
    ListNode* reverseBetween(ListNode* head, int left, int right) {
        ListNode*dummy_head=new ListNode(0);
        dummy_head->next=head;
        ListNode*prev=dummy_head;
        for(int i=0;i<left-1;i++) {
            prev=prev->next;//找到待反转部分最左侧节点的前一个节点
        }
        ListNode*left_node=prev->next;//待反转部分的最左侧节点
        ListNode*right_node=prev;
        for(int i=0;i<right-left+1;i++) {
            right_node=right_node->next;
        }
        //现在right_node是待反转部分的最右侧节点
        ListNode*curr=right_node->next;//找到待反转部分最右侧节点的下一个节点

        //把待反转部分单独抽出来，就回到了反转链表I
        prev->next=nullptr;
        right_node->next=nullptr;
        reverse(left_node);

        //拼接
        prev->next=right_node;
        left_node->next=curr;
        return dummy_head->next;
    }
};

方法二：

不再单独把反转部分单独抽出来，而是找到最左侧节点后直接操作。

cpp 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    void reverse(ListNode*head) {
        ListNode*pre=nullptr;
        ListNode*cur=head;
        while(cur) {
            ListNode*tmp=cur->next;
            cur->next=pre;
            pre=cur;
            cur=tmp;
        }
    }
    ListNode* reverseBetween(ListNode* head, int left, int right) {
        ListNode*dummy_head=new ListNode(0);
        dummy_head->next=head;
        ListNode*prev=dummy_head;
        for(int i=0;i<left-1;i++) {
            prev=prev->next;//找到待反转部分最左侧节点的前一个节点
        }
        ListNode*curr=prev->next;//待反转部分的最左侧节点
        ListNode*nxt;
        for(int i=0;i<right-left;i++) {
            nxt=curr->next;
            //换位
            curr->next=nxt->next;

            //把nxt移到最前面
            nxt->next=prev->next;
            prev->next=nxt;
        }
        return dummy_head->next;
    }
};

每一次操作，除了交换位置之外，还把后面的节点移到最前面，这样就实现了反转。

题目三：2130. 链表最大孪生和 - 力扣（LeetCode）

在一个大小为 n 且 n 为偶数的链表中，对于 0 <= i <= (n / 2) - 1 的 i ，第 i 个节点（下标从 0 开始）的孪生节点为第 (n-1-i) 个节点。

比方说，n = 4 那么节点 0 是节点 3 的孪生节点，节点 1 是节点 2 的孪生节点。这是长度为 n = 4 的链表中所有的孪生节点。

孪生和 定义为一个节点和它孪生节点两者值之和。

给你一个长度为偶数的链表的头节点 head ，请你返回链表的 最大孪生和 。

示例 1：

复制代码

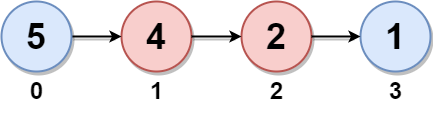
输入：head = [5,4,2,1]
输出：6
解释：
节点 0 和节点 1 分别是节点 3 和 2 的孪生节点。孪生和都为 6 。
链表中没有其他孪生节点。
所以，链表的最大孪生和是 6 。

示例 2：

复制代码

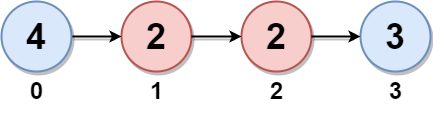
输入：head = [4,2,2,3]
输出：7
解释：
链表中的孪生节点为：
- 节点 0 是节点 3 的孪生节点，孪生和为 4 + 3 = 7 。
- 节点 1 是节点 2 的孪生节点，孪生和为 2 + 2 = 4 。
所以，最大孪生和为 max(7, 4) = 7 。

示例 3：

复制代码

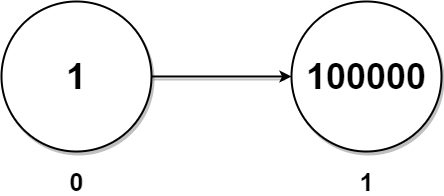
输入：head = [1,100000]
输出：100001
解释：
链表中只有一对孪生节点，孪生和为 1 + 100000 = 100001 。

提示：

链表的节点数目是 [2, 105] 中的偶数。
1 <= Node.val <= 105

方法一：转成数组

这是最简单的方法，把节点值一个个压入数组中，再通过遍历即可。

cpp 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    int pairSum(ListNode* head) {
        vector<int>vec;
        while(head){
            vec.push_back(head->val);
            head=head->next;
        }
        int ans=0;
        for(int i=0;i<vec.size()/2;i++) {
            ans=max(ans,vec[i]+vec[vec.size()-1-i]);
        }
        return ans;
    }
};

方法二：快慢指针+反转链表

面试的时候一般不会让我们直接把链表的节点值放入数组中，因此我们需要思考别的办法。

我们之所以希望使用数组，是因为使用数组可以倒序遍历，而链表是不可以的。但是这种思想给予我们一个很大的启发，我们可以通过快慢指针找到中间位置，与此同时反转链表的前半部分。如果反转后半部分，那么计算孪生和的时候又要从头开始了。因此考虑在慢指针前进的同时反转前半部分链表，这样到达中间位置后，prev和curr再相背而行即可。

cpp 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    int pairSum(ListNode* head) {
        ListNode*slow_prev=nullptr;
        ListNode*slow_curr=head;
        ListNode*fast=head;
        while(fast) {
            fast=fast->next->next; //因为长度为偶数，所以最终fast必然为nullptr，因此while的条件应该是fast不为空，而不是fast->next不为空
            ListNode*tmp=slow_curr->next;
            slow_curr->next=slow_prev;
            slow_prev=slow_curr;
            slow_curr=tmp;
        }
        int ans=0;
        while(slow_curr) {
            //此时slow_curr是后半部分的头节点，slow_prev是前半部分的头节点
            ans=max(ans,slow_curr->val+slow_prev->val);
            slow_curr=slow_curr->next;
            slow_prev=slow_prev->next;
        }
        return ans;
    }
};

这样不仅优化了空间复杂度，而且还没有出现指针走了重复路程的情况。