论文理解 【LLM-回归】—— Decoding-based Regression

• 文章链接：Decoding-based Regression
• 发表：Arxiv
• 领域：LLM 浮点回归
• 一句话总结：本文针对 LLM 的数值回归能力展开深入分析，通过坚实的理论与实证基础，说明通过解码数值 token序列，LLM 可自然地实现点估计与分布建模的统一框架

---

• 摘要：最近的研究表明，语言模型具备进行回归分析的能力，其中数值预测结果会以解码后的字符串形式呈现出来 。在这项研究中，我们为这种能力提供了理论依据，并进一步探讨了任意特征表示条件下，基于因果序列解码模型的数值回归功能。研究发现，尽管这些模型是按照常规方法进行训练的------即通过交叉熵损失来预测下一个词汇------但在标准回归任务中，基于解码器的模型的性能与传统的逐点回归模型相媲美，且这类模型还具备足够的灵活性，能够捕捉到连续的数值分布，例如在密度估计这类任务中

文章目录

• [1. 背景](#1. 背景)
• • [1.1 语言模型的回归能力](#1.1 语言模型的回归能力)
  • [1.2 相关工作与动机](#1.2 相关工作与动机)
  • • [1.2.1 点回归头](#1.2.1 点回归头)
    • [1.2.2 黎曼回归头（直方图分布）](#1.2.2 黎曼回归头（直方图分布）)
    • [1.2.3 解码式回归头](#1.2.3 解码式回归头)
• [2. 本文方法](#2. 本文方法)
• • [2.1 形式化描述](#2.1 形式化描述)
  • [2.2 点估计（Pointwise Estimation）](#2.2 点估计（Pointwise Estimation）)
  • [2.3 密度估计和理论](#2.3 密度估计和理论)
  • • [2.3.1 数值表示](#2.3.1 数值表示)
    • [2.3.2 模型的可学习性](#2.3.2 模型的可学习性)
• [3. 实验](#3. 实验)
• • [3.1 曲线拟合](#3.1 曲线拟合)
  • [3.2 实际回归任务](#3.2 实际回归任务)
  • [3.3 密度估计](#3.3 密度估计)
  • [3.4 消融实验](#3.4 消融实验)
• [4. 总结](#4. 总结)

1. 背景

1.1 语言模型的回归能力

• 由于语料中存在数值文本，经过预训练的 LLM 天然具有一定的数值回归能力，早期研究发现可以通过 in-context learning 的方式控制 ChatGPT 等 LLM 服务执行回归任务，且这种能力可通过微调或继续预训练得到强化
• 由于微调后可用作 RL 奖励模型，LLM 数值回归近期得到了深入研究，现有工作主要可分为以下两类
  1. 自回归类方法：将数值目标视作文本生成任务，逐 token 预测数值表达，或将数值映射为离散类别进行预测 。训练时通常采用交叉熵损失，然后在推理阶段采用自回归解码预测数值（标准贪心/采样解码、回归感知类解码）。微调时可通过在标准 CE 损失中引入数值敏感项来增强回归能力，相关文章有 NTL 和 NTIL 等
  2. 预测头类方法：在LLM输出特征上增加一个回归头 ，用 MSE 等回归损失训练/微调该头以直接预测数值。相关文章有基于 pooled embedding 特征的 Rankt5 和基于最后一个 token 特征的 AutoMQM 等。这个回归头也可以设置为某种先验分布
• 虽然自回归类方法存在明显问题，比如 token 间缺乏数值归纳偏置、一个浮点数的特征可能表示为多个连续 embedding 等（将 1.23 表示为 <1><.><2><3>），作者认为基于解码的自回归类方法可能更具灵活性，因为它们能够在实数域 R \mathbb{R} R 上近似表示任意数值分布，而无需显式的归一化过程，这种权衡关系值得进行实证研究

1.2 相关工作与动机

• 形式化地讲，对于任意样本 ( x , y ) (x,y) (x,y)，其中 x x x 是特征向量， y y y 是实数，回归模型的性能由模型如何处理 x x x 和模型如何刻画输出 y y y 决定（例如 y y y 的形式和对条件分布 p ( y ∣ x ) p(y|x) p(y∣x) 的建模假设）。从这两个角度出发，作者顾了此前与 "回归头" 相关的工作

1.2.1 点回归头

• 最常用的点回归头（point regression head）通常由一个可学习的投影 ϕ ( x ) \phi(x) ϕ(x) 和可选的确定性变换（如使用 sigmoid 函数压缩取值范围）构成 。这类方法要求 y y y 被归一化到某个固定空间，以确保训练稳定
• 在概率输出的情形下，可以使用参数化分布头 。例如假设数据服从高斯分布，模型需要引入可训练的线性层把特征 ϕ ( x ) \phi(x) ϕ(x) 映射到 μ \mu μ 和 σ \sigma σ。现实情况中数据的真实分布可能很难假设，为提高灵活性，可以将参数化头扩展为有限或无限高斯混合模型，这些混合技术可以看作概率密度估计 领域中的一种做法，即通过多个简单的基分布来近似复杂分布

  • 密度估计是统计学和机器学习中的一个基础问题，通过利用从某个随机变量中抽取的样本估计其概率密度。
  • 核密度估计（Kernel Density Estimation, KDE）是一种经典的非参数化方法，其基本思想是不要假设数据一定服从某种分布（比如高斯），而是用样本自身"堆"出一个分布。对每个样本，在其位置放置一个小的"核函数"（比如高斯核），整个密度估计由所有核函数叠加后平滑得到

1.2.2 黎曼回归头（直方图分布）

• Riemann 回归头使用了被广泛使用的分段常数（Riemann）基函数，其把数值范围划分成若干区间（bins） { y 1 , . . . , y n } ⊂ R \{y_1,...,y_n\}\sub\mathbb{R} {y1,...,yn}⊂R，模型输出的 logits 经过 softmax 转换为真实值落在各区间的概率，从而构成一个 "分布头"（distribution head）
  p ( y i ∣ x ) = Softmax ( i ) ( ϕ ( x ) T ⋅ w ) p(y_i|x) = \text{Softmax}(i)\big(\phi(x)^T\cdot w\big) p(yi∣x)=Softmax(i)(ϕ(x)T⋅w) 其中 ϕ ( x ) \phi(x) ϕ(x) 是编码器输出的样本 x x x 的特征向量， w w w 是可学习的分 bin 权重矩阵 这种方法在 RL 改进 Q-Learning 的系列工作中得到了广泛使用，但提升精度需要细化分 bin 数，因此需要大量数据进行训练

1.2.3 解码式回归头

• Decoder 解码式回归头是 LLM 默认使用的数值回归头。其将数值目标视作文本生成任务，通过逐 token 预测字符来表示浮点数，并使用交叉熵损失进行标准监督微调。直觉上这种做法是不合理的，因为在这种情况下并不存在数值距离概念
• 目前几乎没有在理论和建模能力上对这种解码式回归头进行分析的工作，但作者发现 解码式回归头可以看作黎曼回归头的一种扩展，具有拟合理论保证，且有能力实现良好的回归性能 。作为一篇分析+实证工作，本文并不提出新方法，而是聚焦于逐步解码这种通用回归机制，具体地：
  1. 本文的研究对象是一种 Encoder-Decoder 模型，不关注使用哪种 Encoder 得到特征表示 ϕ ( x ) \phi(x) ϕ(x)，而是聚焦于输出端使用的回归头类型 实验中的 encoder 是一个 小型 MLP，作者刻意控制 encoder 能力以便聚焦输出机制
  2. 本文的目标是给出 decoder head 的理论可行性，并与 point regression head、Riemann heads 进行实验对比，证明其在有限样本下的有效性与表达灵活性
  3. 实验范围聚焦在 tabular regression 与一维 density estimation，所有任务都是结构化数据或函数拟合。本文聚焦于回归机制，不局限于 LLM

2. 本文方法

2.1 形式化描述

• 回归任务定义 ：

  • 在特征 x ∈ R D x\in\mathbb{R}^D x∈RD 和回归值 y ∈ R y\in\mathbb{R} y∈R 上存在真实条件分布 p ( y ∣ x ) p(y|x) p(y∣x)，要基于训练数据 { ( x i , y i ) } i = 1 N \{(x_i,y_i)\}{i=1}^N {(xi,yi)}i=1N 学习参数化模型 p θ ( y ∣ x ) p\theta(y|x) pθ(y∣x) 进行近似
  • 针对 LLM，给定词表 V V V，模型将 y ∈ R y\in\mathbb{R} y∈R 映射到定长 token 序列 ( t 1 , . . . , t K ) ∈ V K (t_1,...,t_K)\in\ V^K (t1,...,tK)∈ VK

• 自回归训练范式 ：LLM 对所有序列 token 应用标准交叉熵损失。数值回归场景下，给定模型 p θ p_\theta pθ 与目标 y = ( t 1 , . . . , t K ) y=(t_1,...,t_K) y=(t1,...,tK)，单次交叉熵损失表示为（省略条件 x x x）
  H ( y , p θ ) = ∑ k = 1 K ∑ t ^ k ∈ V − 1 ( t ^ k = t k ) log ⁡ p θ ( t ^ k ∣ t 1 , ... , t k − 1 ) H\left(y, p_{\theta}\right)=\sum_{k=1}^{K} \sum_{\hat{t}{k} \in V}-\mathbf{1}\left(\hat{t}{k}=t_{k}\right) \log p_{\theta}\left(\hat{t}{k} \mid t{1}, \ldots, t_{k-1}\right) H(y,pθ)=k=1∑Kt^k∈V∑−1(t^k=tk)logpθ(t^k∣t1,...,tk−1)

• Tokenize方法 ：有两种将浮点数表示为 token 序列的方式，如下表所示

  	归一化Tokenize	非归一化Tokenize
  概述	将输出取值区间归一化到 [ 0 , 1 ] [0,1] [0,1]， 再按固定进制转换展开为小数位 token 序列，分bin固定为1	不做归一化，用科学计数法形式将符号、指数和尾数分别分词。输出表示为 s ⋅ B e ⋅ m s\cdot B^e\cdot m s⋅Be⋅m，其中符号 s ∈ { + , − } s\in\{+,-\} s∈{+,−}，指数 e ∈ Z e\in\mathbb{Z} e∈Z，维数 m ∈ [ 0 , B ) m\in[0,B) m∈[0,B)
  通用性	需确定输出取值范围	需设置浮点表示超参数，包括进制 B B B，指数位数 E E E 和尾数尾数 M M M
  优点	表示简单，训练稳定，token分布集中	无需归一化，跨任务表示能力强
  缺点	若数值区间跨越多个数量级，表示误差会增大	token稀疏，符号与指数组合难学
  例子	123.4 ⟶ 归一化 0.1234 ⟶ 分词 ⟨ 1 , 2 , 3 , 4 ⟩ 123.4 \stackrel{归一化}{\longrightarrow}0.1234\stackrel{分词}{\longrightarrow}\langle1,2,3,4\rangle 123.4⟶归一化0.1234⟶分词⟨1,2,3,4⟩	123.4 = 1.234 × 1 0 2 ⟶ 分词 ⟨ + , 2 , 1 , 2 , 3 , 4 ⟩ 123.4=1.234\times 10^2 \stackrel{分词}{\longrightarrow}\langle+,2,1,2,3,4\rangle 123.4=1.234×102⟶分词⟨+,2,1,2,3,4⟩

• 模型架构：任意自回归模型都可以使用，只要能约束其输出，强制生成合法数值序列即可

2.2 点估计（Pointwise Estimation）

• 很多情形中，我们只对模型分布的标量统计量感兴趣，这和传统点回归头输出一个数值直接匹配。本节讨论从模型输出的条件分布 p ( y ∣ x ) p(y|x) p(y∣x) 中导出点估计值的方法

• 通常我们关注以下点估计量。每种估计量都有多种具体的计算方法，作者将其作为超参数在不同应用中调优

  估计量	损失	LLM 生成方法	特点
  均值	MSE	对 p ( y ∣ x ) p(y|x) p(y∣x) 支持集加权求和 / RAFT	平滑可微、但对异常值敏感；在非归一化Tokenize中易被极端输出拉偏
  众数	0-1 loss	Beam search / top-k / top-p 解码	稳健性强、不受极端值影响，估计更平滑但计算略复杂
  中位数	MAE	本文使用 Harrell--Davis 估计器	取概率最大的输出序列；直观但易陷入局部最优，对分布形状敏感

2.3 密度估计和理论

2.3.1 数值表示

• 为便于分析，只考虑归一化 tokenize 方法，设浮点数回归数值区间已缩放平移到 [ 0 , 1 ] [0,1] [0,1]，定义操作 λ k : [ 0 , 1 ) → { 0 , 1 } k \lambda_k: [0,1)\to \{0,1\}^k λk:[0,1)→{0,1}k 为提取小数点后的前 k k k 个二进制小数位 ，把 λ k \lambda_k λk 同时视作序列 0. b 1 b 2 ... b k 0.b_1b_2\dots b_k 0.b1b2...bk 和其代表的实数 ∑ i = 1 k b i 2 − i \sum_{i=1}^kb_i 2^{-i} ∑i=1kbi2−i

  这里为简便起见使用二进制，即 V = { 0 , 1 } V=\{0,1\} V={0,1}，但本节分析同样适用于任意进制

  λ k \lambda_k λk 实质上将 [ 0 , 1 ] [0,1] [0,1] 区间离散化为 2 k 2^k 2k 个分桶 { B j } j = 0 2 k − 1 \{B_j\}{j=0}^{2^k-1} {Bj}j=02k−1，其中 B j = [ j 2 − k , ( j + 1 ) 2 − k ) B_j=[j2^{-k},(j+1)2^{-k}) Bj=[j2−k,(j+1)2−k)。设回归任务的真实条件分布 p ( y ∣ x ) p(y|x) p(y∣x) 记作 f ( y ) : [ 0 , 1 ] → R f(y):[0,1]\to\mathbb{R} f(y):[0,1]→R，真实回归值落入桶 B j B_j Bj 的概率可以表示为： P ( x ∈ B j ) = ∫ B j f ( y ) d y \mathbb{P}(x\in B_j) = \int{B_j} f(y)dy P(x∈Bj)=∫Bjf(y)dy

  k = 1 k=1 k=1 时，直方图由两个桶组成 [ 0 , 1 2 ) , [ 1 2 , 1 ) [0,\frac{1}{2}), [\frac{1}{2},1) [0,21),[21,1)，对应的序列为 0.0 和 0.1
  k = 2 k=2 k=2 时，直方图由两个桶组成 [ 0 , 1 4 ) , [ 1 4 , 1 2 ) , [ 1 2 , 3 4 ) , [ 3 4 , 1 ) [0,\frac{1}{4}), [\frac{1}{4},\frac{1}{2}), [\frac{1}{2},\frac{3}{4}), [\frac{3}{4},1) [0,41),[41,21),[21,43),[43,1)，对应的序列为 0.00、0.01、0.10 和 0.11

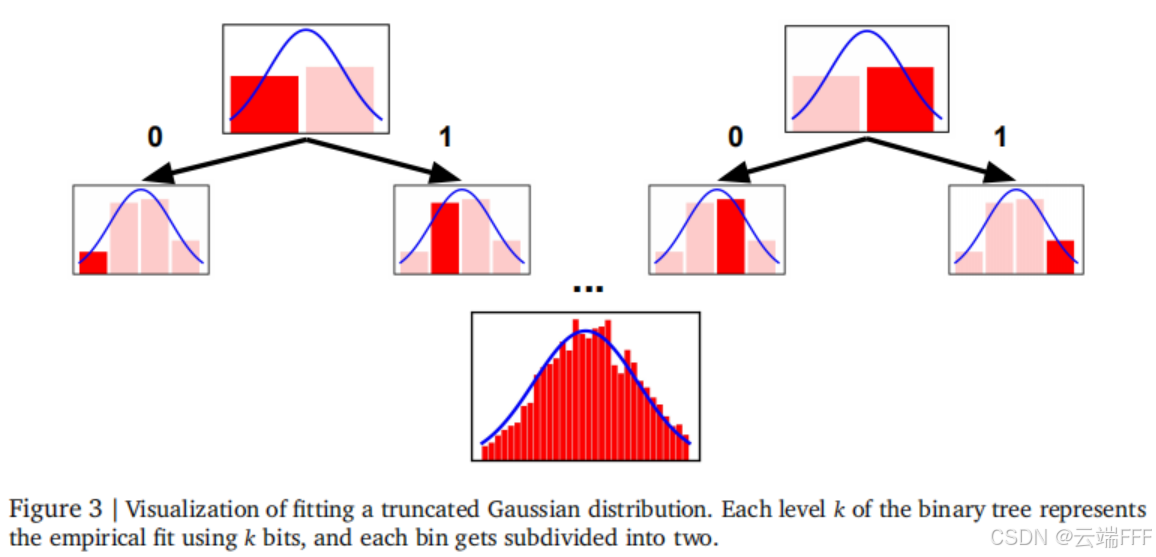
• 这种表示方式可以看作一个二叉树结构，根节点代表完整区间 [ 0 , 1 ] [0,1] [0,1]，其下第 k k k 层具有 2 k 2^k 2k 个 bin。对于解码式回归头方法来说，模型 p θ p_\theta pθ 同时学习了 k k k 个针对真实数值分布 f f f 的直方图估计，当模型逐位自回归解码时，预测被不断细化 。 下图展示了该机制在拟合截断高斯分布的过程
  

• 将 1.2.3 节所述的 LLM 解码式数值回归方法记为 Decoder，将 1.2.2 节所述的直方图数值回归方法记为 Riemann，对比分析可见 Riemann 是传统 Decoder 方法的一个 k = 1 k=1 k=1 的特例，二者关系如下：

  • 词表尺寸为 2 解码 k k k 步的 Decoder 方法，和词表尺寸为 2 k 2^k 2k 解码 1 步的 Riemann 方法表示能力相同（离散区间分辨率均为 2 k 2^k 2k）
  • Decoder 每生成一个 token 时都将区间二分，能以指数方式提升分辨率，不需要指数级的 bin 数量

2.3.2 模型的可学习性

• 将模型的可学习性作定义为 K-bit 普适性（K-bit universality）：令 H ( p , q ) = E y ∼ p [ − log ⁡ q ( y ) ] H(p,q)=\mathbb{E}{y\sim p}[-\log q(y)] H(p,q)=Ey∼p[−logq(y)] 表示离散分布 p , q p,q p,q 之间的交叉熵。若对于所有定义在 k k k 位字符串（ 2 k 2^k 2k 个数值表示）上的离散分布，都有
  min ⁡ θ H ( p , p θ ) = H ( p , p ) \min\theta H(p,p_\theta) = H(p,p) θminH(p,pθ)=H(p,p) 则称参数化模型 p θ p_\theta pθ 为 K-bit 普适的。直观理解，若模型 p θ p_\theta pθ 能通过 SGD 精确拟合任意定义在 2 k 2^k 2k 个类别上的离散分布，则它是 K-bit 普适的

• 基于以上定义，作者推导了直方图估计的偏差--方差分解公式：假设解码式回归模型 p θ : { 0 , 1 } K → Δ 2 K p_\theta: \{0,1\}^K\to\Delta_{2^K} pθ:{0,1}K→Δ2K 是 K-bit 普适的，通过对剩余位边缘化定义 p θ p_\theta pθ 下前 k k k 序列的概率为：
  p θ K ( ( b 1 , ... , b K ) ) = ∑ b k + 1 , ... , b K p θ ( ( b 1 , ... , b K ) ) p_{\theta}^{K}\left(\left(b_{1}, \ldots, b_{K}\right)\right)=\sum_{b_{k+1}, \ldots, b_{K}} p_{\theta}\left(\left(b_{1}, \ldots, b_{K}\right)\right) pθK((b1,...,bK))=bk+1,...,bK∑pθ((b1,...,bK)) 这里 p θ k p_\theta^k pθk 是对自回归解码执行恰好 k k k 步时得到的 k k k-bit 字符串分布 。令真实概率密度 f : [ 0 , 1 ] → R f:[0,1]\to \mathbb{R} f:[0,1]→R 为任意光滑的一维密度函数，令 { Y 1 , ... , Y N } \{Y_1,\dots,Y_N\} {Y1,...,YN} 为来自 f f f 的 i.i.d. 抽样，定义 θ ^ \hat{\theta} θ^ 为在截断 K-bit 序列上的最大似然估计器
  θ ^ ( Y 1 , ... , Y N ) = arg ⁡ min ⁡ θ 1 N ∑ n = 1 N − log ⁡ p θ ( λ K ( Y n ) ) \hat{\theta}\left(Y_{1}, \ldots, Y_{N}\right)=\arg \min {\theta} \frac{1}{N} \sum{n=1}^{N}-\log p_{\theta}\left(\lambda_{K}\left(Y_{n}\right)\right) θ^(Y1,...,YN)=argθminN1n=1∑N−logpθ(λK(Yn)) 定义风险 R R R 为真实密度 f f f 与其估计 f ^ \hat{f} f^ 之间的均方积分误差
  R ( f , f ^ N ) = E Y 1 , ... , Y N ∼ f [ ∫ 0 1 ( f ( y ) − f ^ N ( y ) ) 2 d y ] R\left(f, \hat{f}{N}\right)=\mathbb{E}{Y_{1}, \ldots, Y_{N} \sim f}\left[\int_{0}^{1}\left(f(y)-\hat{f}{N}(y)\right)^{2} d y\right] R(f,f^N)=EY1,...,YN∼f[∫01(f(y)−f^N(y))2dy] 其中概率密度估计定义为 f ^ N k ( y ) = 2 k p θ ^ ( Y 1 , ... , Y N ) k ( λ k ( y ) ) \hat{f}{N}^{k}(y)=2^{k} p_{\hat{\theta}\left(Y_{1}, \ldots, Y_{N}\right)}^{k}\left(\lambda_{k}(y)\right) f^Nk(y)=2kpθ^(Y1,...,YN)k(λk(y))，均方积分误差满足下式
  R ( f , f ^ N k ) ≈ 2 − 2 k 1 12 ∫ 0 1 f ′ ( y ) 2 d y + 2 k N , ∀ k ≤ K (1) R\left(f, \hat{f}{N}^{k}\right) \approx 2^{-2 k} \frac{1}{12} \int{0}^{1} f^{\prime}(y)^{2} d y+\frac{2^{k}}{N}, \quad \forall k \leq K \tag{1} R(f,f^Nk)≈2−2k121∫01f′(y)2dy+N2k,∀k≤K(1) 注意该定理的唯一要求是模型是 K-bit 普适的，Decoder 和 Riemann 方法都能表示 2 k 2^k 2k 个 bin 概率分布，都能实现 K-bit 普适，二者都适用于该定理 。为简化起见，以下分析假设解码时使用和训练相同的 k = K k=K k=K

• 式 (1) 是直方图估计误差的 偏差--方差分解 公式，可见误差由两部分组成：

  1. 偏差（平方）项 ：第一部分 2 − 2 k 1 12 ∫ 0 1 f ′ ( y ) 2 d y 2^{-2 k} \frac{1}{12} \int_{0}^{1} f^{\prime}(y)^{2} d y 2−2k121∫01f′(y)2dy 代表解码过程中使用 2 k 2^k 2k 个分 bin 将连续的 f ( y ) f(y) f(y) 函数离散化所引起的偏差的平方。随离散分辨率 2 k 2^k 2k 增大而下降
  2. 方差项 ：第二部分 2 k N \frac{2^k}{N} N2k 是与样本数量 N N N 和分bin数量 2 k 2^k 2k 有关的方差带来的误差。随离散分辨率 2 k 2^k 2k 增大而上升（样本分布更稀、方差更高）
     

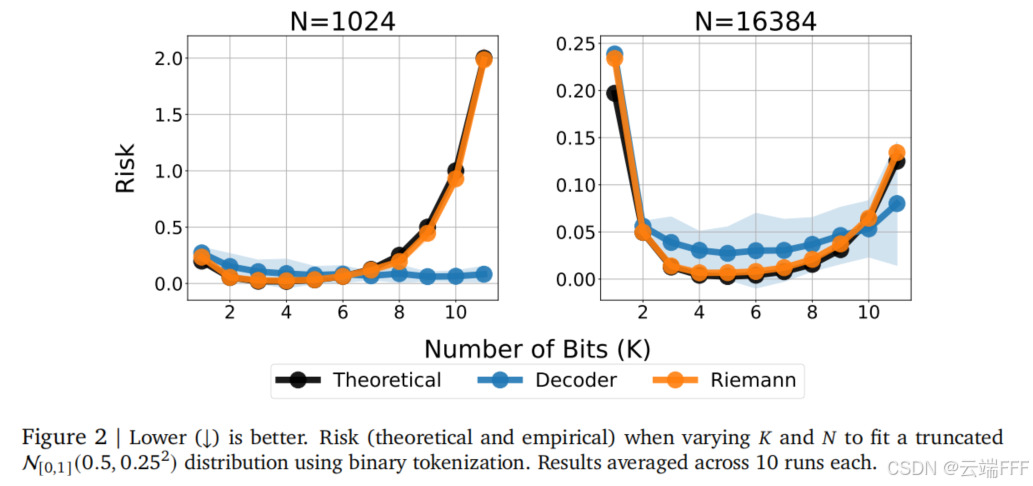
  给定少量（1024）和大量（16384）训练样本，考察误差 R R R 和 K K K 的关系，如图可见：

  1. 随着分 bin 数提升，总体误差先下降再上升，这意味着 K K K 较小时偏差项主导， K K K 较大时方差项主导；

  2. 当样本数 N N N 相对分 bin 数 K K K 严重不足时（左图），Decoder 方法性能更好，而 Riemann 方法和理论风险保持一致。作者认为这是因为

     • Riemann 方法显式地考虑 2 K 2^K 2K 个 bin 概率参数，每个 bin 独立学习，当样本少时很多 bin 样本不足，导致方差大
     • Decoder 方法通过自回归结构共享参数 （即在不同 bit 层级间共享 p θ p_\theta pθ 参数），使模型天然会学习到平滑的层级结构，这是一种隐式平滑先验，它倾向于让相邻区间（相似的 token 序列）的生成概率相近，从而抑制噪声，使样本不足时方差减小 可以这样理解，Decoder 方法把 token 序列 ( t 1 , . . . , t K ) (t_1,...,t_K) (t1,...,tK) 的概率表示为一系列 p θ p_\theta pθ 条件概率的连乘，因此 0011001 和 0011000 几乎共享相同的输入 p θ ( t i ∣ t < i , x ) p_\theta(t_i|t_{<i},x) pθ(ti∣t<i,x)，这使得 2 K 2^K 2K 个 bin 中相邻的 bins 概率相近

  3. 当样本数 N N N 相对分 bin 数 K K K 充足时（右图），Riemann 方法性能更好，作者认为这是因为

     • Riemann 是无平滑约束的估计其，其不存在 Decoder 方法层次化解码导致的隐式平滑，因此可以在更大的假设空间中进行优化
     • Decoder 的强制参数共享导致模型容量降低，牺牲了优化灵活性，导致训练样本充足时偏差更高

• 总结：Decoder 的自回归解码方法是一种学习细粒度分 bin 的高效方法，其利用隐式平滑归纳偏置，在训练样本较少时拟合方差更低，效果更好；但这种归纳偏置也降低了模型表示容量，在训练样本多时偏差较高，效果不如Riemann 方法

3. 实验

• 实验主要目标如下：
  1. 证明 Decoder head 方法可以有效地替代常见的点式回归头
  2. 验证 Decoder head 方法在任意实数分布上的密度估计能力
  3. 研究解码器规模以及序列特定方法（如误差校正）对性能的影响
• 为了排除 Encoder 的影响，所有实验都使用了相同的小规模 MLP 作为 Encoder，其参数量不到总参数量 10%，从而尽量排除其在表征学习方面的影响

3.1 曲线拟合

• 使用无限训练数据，未归一化的 Decoder head 能成功拟合多种 1D 函数形状，而点式回归头在相同条件下表现不佳
  
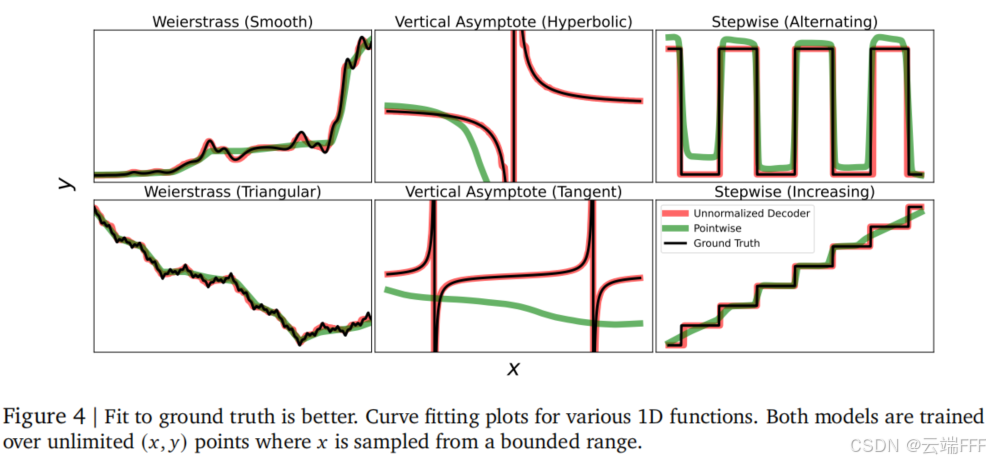
  未归一化的 Decoder head 由于能表达极宽的 y y y 范围，样本充足时可以有效拟合，而点回归头有以下问题
  1. 需对输出 y y y 进行归一化，当 y y y 具有极高或无界的数值范围时会导致数值不稳定；
  2. 难以建模变化率极高（Lipschitz 常数大）的函数
• 作者还使用 BBOB 基准测试考察了各种方法拟合多维连续目标函数的能力，
  
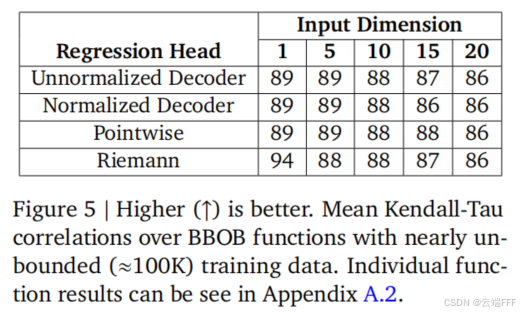
  可见未归一化和归一化的 Decoder 方法都能充分拟合不同输入维度上的函数，同时也能与点回归基线和 Riemann 基线相媲美

3.2 实际回归任务

• 用真实世界的 OpenML 数据集中的 OpenML-CTR23 和 AMLB 基准任务进行测试。发现在相同数量的有限训练样本下，未归一化解码器的表现与常规点式回归头相当甚至更优
  

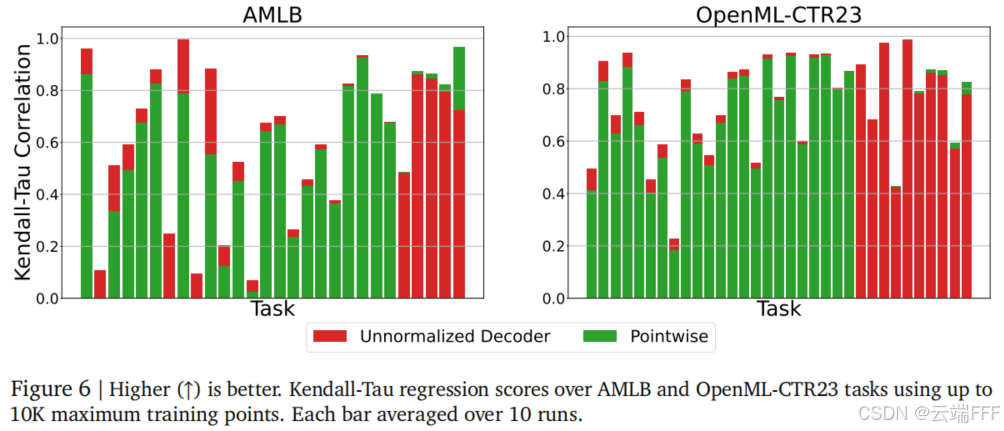
• 进一步比较归一化 Decoder 方法、Riemann 方法、点回归头在不同训练样本量下的表现
  

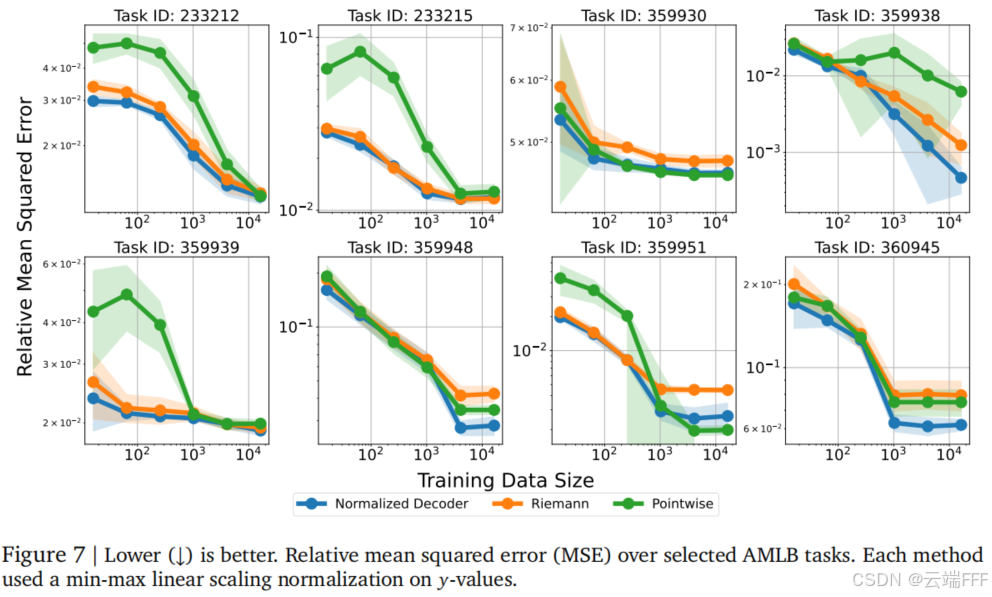
  1. Riemann 方法在若干任务中表现出数据低效性
  2. 在高数据区（约 10⁴ 样本）时，回归头在部分任务过早地性能饱和
  3. 在低数据区（约 10¹ 样本）时，理论上解码器应更困难（因需学习数值 token 表示），但实际上点回归头表现更差，主要原因是数值不稳定
  4. 为避免极高的 MSE，回归头在欠训练时必须附加 Sigmoid 激活，将输出强制限制在 [0,1] 范围。

3.3 密度估计

• 在无限训练数据下，Decoder 方法能很好地重现真实分布 𝑝 ( 𝑦 ∣ 𝑥 ) 𝑝(𝑦|𝑥) p(y∣x)，但会出现轻微离群点噪声 。不过基线方法汇中也存在类似的噪声。降低采样温度可以去除噪声，但会牺牲表达性。作者发现默认温度 1.0 的采样最能无偏匹配 𝑝 ( 𝑦 ∣ 𝑥 ) 𝑝(𝑦|𝑥) p(y∣x)
  
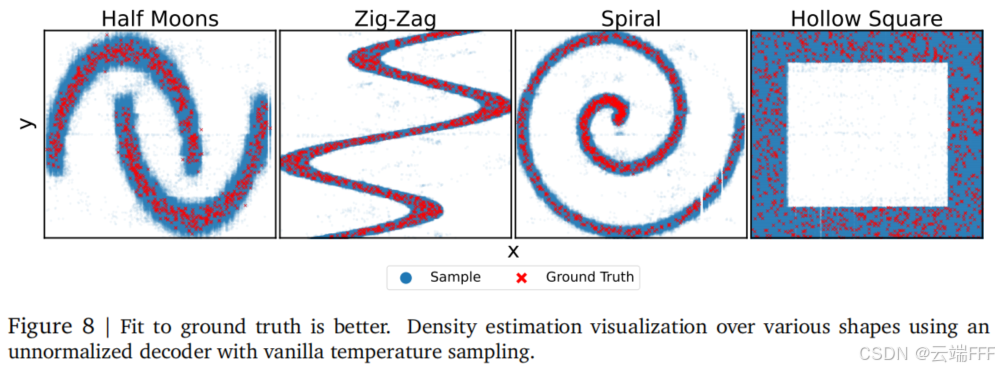
• 下表列出了 UCI 回归数据库部分数据集上的负对数似然（NLL）结果
  
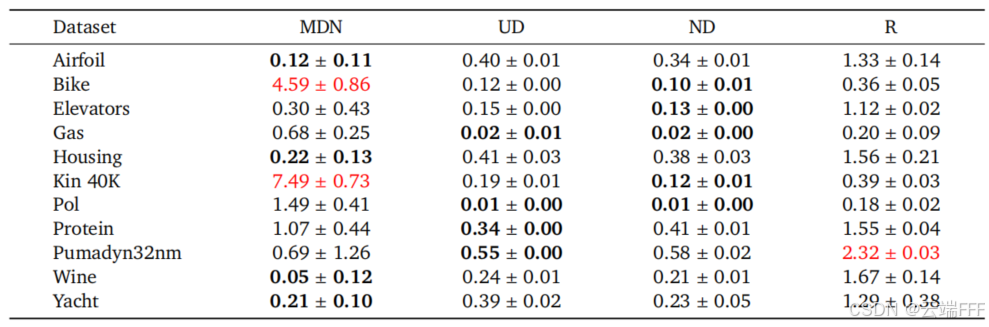
  结果显示：
  1. MDN 性能波动大，部分任务优异，但部分任务极差
  2. 归一化与未归一化解码器在各任务上表现稳定（NLL < 0.7）
  3. Riemann 方法在大部分任务中表现最差

3.4 消融实验

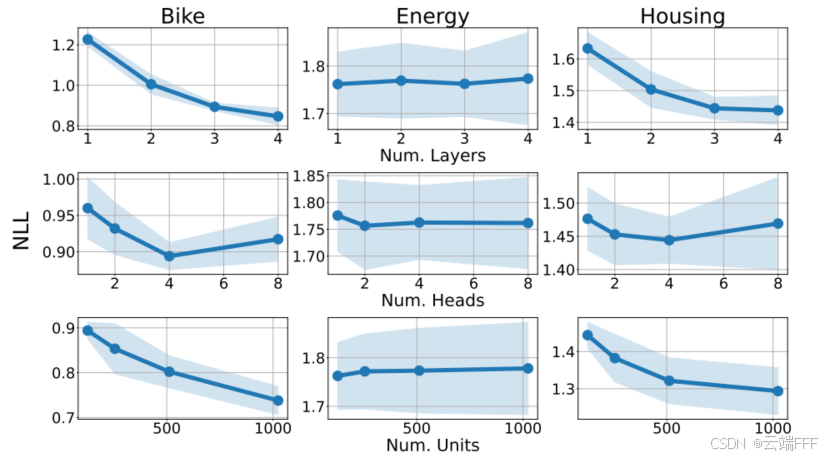
• 作者考察了解码器规模的影响，这里控制了 tokenize 设定，通过改变层数、注意力头数和隐藏层尺寸调整参数规模。如图所示，较大的解码器在一定范围内有助性能提升，但过大则会导致过拟合
  
• 作者考虑了 LLM 研究中误差纠正方法的影响。训练模型重复推理若干次，即连续输出 ( t i , . . . , t k , t 1 ′ , . . . , t k ′ ) (t_i,...,t_k,t_1',...,t_k') (ti,...,tk,t1′,...,tk′)，推理时对每个位置 k k k 进行多数投票
  
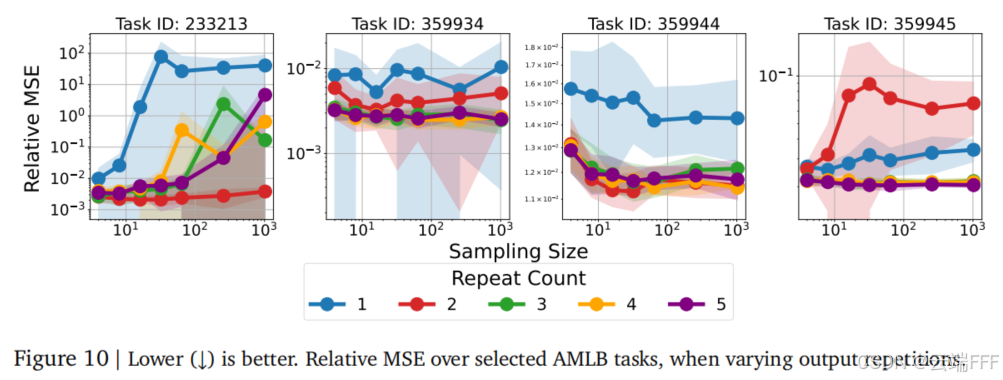
  1. 随着采样数量增多，抽到极端离群值的概率上升，误差随之增大
  2. 通过训练模型重复输出，可显著降低误差并改善随样本数量的扩展性；但重复过多会增加学习难度
  3. 并非所有误差校正技术都能提升性能

4. 总结

• 基于解码的回归（decoding-based regression）不直接预测连续值，而是将数值表示为一串离散 token，让自回归语言模型的解码器输出这些 token，从而学习条件分布 p θ ( y ∣ x ) p_\theta(y|x) pθ(y∣x) 。本文发现基于解码的回归头方法可以看作使用 Riemann 回归头得到直方图分布的一种序列化、层次化的扩展 ，在数值范围大、噪声复杂或数据较少的情形相比传统点回归头和 Riemann 回归头有优势，为 "语言模型能做数值回归" 提供了理论基础
• 优点：
  1. 本文证明这种方法可以逼近任意一维密度的理论界
  2. 能自然地进行密度估计，这意味着它不仅可以输出均值或中位数，还可以直接进行分布采样（sampling）、不确定性估计、多峰建模等操作
  3. 可处理任意尺度或无界输出，通过模仿 IEEE-754 浮点格式，可以用符号位 + 指数位 + 尾数位的形式自然地表示极大的实数范围。适于处理高斜率函数，且避免了归一化导致的数值不稳定问题
  4. 多步解码引入了隐式平滑先验，在训练数据不足时数据效率比 Riemann 方法更高
  5. 可以自然地和 LLM 中的采样 tirck 结合，可以兼容现有 LLM 训练范式
• 缺点：
  1. 需要学习数值 token 表示，比点回归头收敛困难一些
  2. 多步解码导致求解速度慢
  3. 多步解码引入了隐式平滑先验，减小了模型容量，在训练数据充足时性能上限比 Riemann 方法略低
• 发展方向
  1. 改进 Tokenize 方案
  2. 分段常数以外的其他基函数分布