ref:An Efficient Solution to theFive-Point Relative Pose Problem
1. 问题描述
对极几何是算法的基础,用来描述两个相机视图之间的几何关系。
-
基本矩阵: 一个 3x3 的秩为 2 的矩阵,包含了两个相机的内参和相对位姿(旋转 R 和平移 t)信息,满足如下方程,其中 x 和 x' 是一对匹配的特征点在两个图像上的归一化相机坐标(或像素坐标):x'ᵀ * F * x = 0
-
本质矩阵: 一个 3x3 的秩为 2 的矩阵,假设相机已经被标定(已知内参矩阵 K),矩阵只包含相对位姿信息(R 和 t)。它与基本矩阵的关系是:E = K'ᵀ * F * K,约束方程是:x'ᵀ * E * x = 0 (这里的 x 是归一化相机坐标)
-
最终目标:从一系列匹配点对 (x, x') 中,求解出 E 或 F,然后从 E 或 F 中分解出旋转矩阵 R 和平移向量 t。
2. 五点法原理
作为视觉SLAM领域的主流算法,非常适用于已知内参的相机(如手机、自动驾驶汽车上的相机),并且在任何场景下(包括看似"退化"的场景)都需要鲁棒估计位姿的情况。
-
求解本质矩阵 E:五点法专门用于求解本质矩阵 E,直接工作在已知相机内参的前提下,使用归一化相机坐标。
-
自由度:本质矩阵 E 有 5 个自由度(3个来自旋转,2个来自平移方向,平移的尺度无法确定),理论上最少需要 5 对匹配点来求解。
-
数学过程:将 x'ᵀ * E * x = 0 方程展开,虽然 E 有 9 个元素,但由于尺度不变性和内在约束(秩为 2,行列式为 0),它只有 5 个自由度,每个点对可以提供一个方程,用 5 个点构建一个线性方程组,但由于方程是非线性的,最终会转化为一个 10次方程的求解问题,最多可以得到 10 个可能的实数解。
-
筛选正确解:将这 10 个可能的 E 矩阵代入更多的匹配点,选择那个使得大部分点满足 x'ᵀ * E * x ≈ 0 的解。
-
分解位姿:从最终确定的 E 中,通过 SVD 分解恢复出 4 组可能的 (R, t) 组合。再通过点必须在两个相机前方(正深度) 的约束筛选出唯一正确的位姿。
3. 对比其他点数
-
八点法:作为最简单的线性方法,是OpenCV视觉库的标准实现。原理是将 x'ᵀ * F * x = 0 或 x'ᵀ * E * x = 0 方程改写为关于矩阵元素的线性方程,每个点对提供一个线性方程,F 有 7 个自由度,但八点法通过最小二乘直接求解,因此,需要至少 8 个点来避免欠定问题,无法处理纯旋转或所有点共面的退化场景。
-
七点法:使用 7 对点,可以构建一个 7x9 的矩阵,解是 2维零空间的基础向量 F1 和 F2 的线性组合:F = α * F1 + (1-α) * F2。利用 F 矩阵秩为 2 的约束 det(F) = 0,代入线性组合得到一个关于 α 的三次方程,最多可得到 3 个实数解,然后从最多3个解中筛选出正确的 F,同样无法处理退化场景。
-
六点法:用于在已知部分运动参数的情况下,减少了自由度,从而可以用更少的点求解。比如,在平面假设下,使用 6 个点通过最小二乘来更鲁棒地估计单应性矩阵 H,然后从 H 中分解出 R 和 t
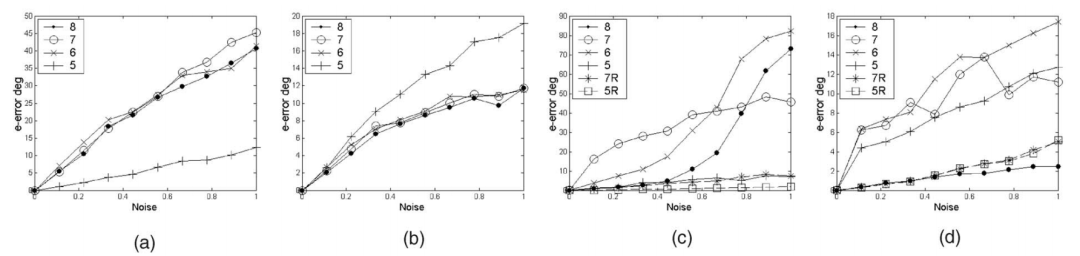
默认条件下,不同点数平移误差随噪声变化的对比结果:a. 最小值横向运动案例b. 最小值纵向运动案例c. 100点横向运动案例d. 100点纵向运动案例