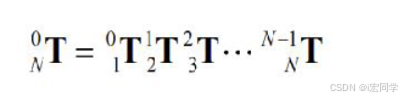文章目录
- 1.坐标系和位姿变换
-
- [1.1 坐标系](#1.1 坐标系)
- [1.2 位姿变换](#1.2 位姿变换)
- [1.3 坐标系之间的转换与链式计算](#1.3 坐标系之间的转换与链式计算)
- 问题:
1.坐标系和位姿变换
1.1 坐标系
对于坐标系有很多种,常见的三轴直角坐标系就是笛卡尔坐标系,对于机器人、机械臂的应用来说,又分世界坐标系、本体坐标系、关节坐标系;
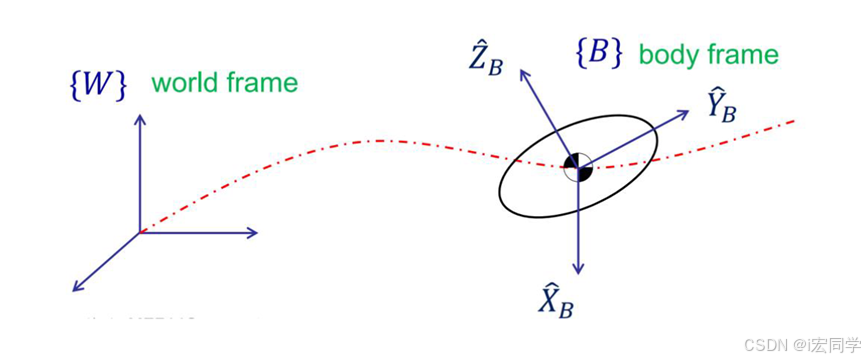
该图描述的就是世界坐标系和本体坐标系,对于关节坐标系,跟随关节的位置和姿态进行变化,与本体坐标系相似。
1.2 位姿变换
齐次矩阵(4x4)表示位姿
位姿=位置+姿态
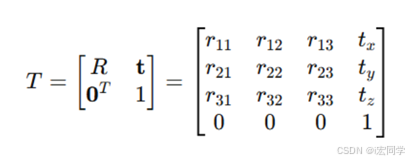
左上3×3子矩阵:旋转分量
右上3×1子矩阵:平移分量
最后一行:[0,0,0,1]保持奇次性
平移、旋转(欧拉⻆、四元数)
- 平移:

- 旋转:
(1)欧拉角
概念:通过绕三个坐标轴的连续旋转表示姿态
常用形式:
ZYX欧拉角:先绕Z轴,再绕Y轴,最后绕X轴
RPY角(Roll-Pitch-Yaw):滚转-俯仰-偏航
优点:直观,易于理解
缺点:存在万向节死锁问题
(2)四元数
概念:⽤四个数表⽰旋转(q₀,q₁,q₂,q₃)
数学形式:q=q₀+q₁i+q₂j+q₃k
优点:⽆万向节死锁 计算效率⾼ 插值平滑(球⾯线性插值)
缺点:不够直观,理解难度⼤
1.3 坐标系之间的转换与链式计算
点P从坐标系A到坐标系B的转换:
具体步骤:

问题:
(1)为什么需要用⼀个整体的"齐次矩阵"来表示位姿,而不是分开用旋转和位移?
分开用旋转和位移,在进行连续变换时需要分别处理旋转和平移,且在进行连续变换时需要分别处理旋转和平移,用⼀个整体的"齐次矩阵"来表示位姿,有如下好处:

(2)如果一个点在A坐标系下有坐标,我们如何把它转换到 B坐标系?
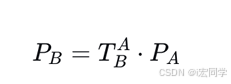
利用上面公式进行转换
-
确定A坐标系相对于B坐标系的位姿
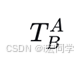
-
将点P在A下的坐标表示为齐次坐标:
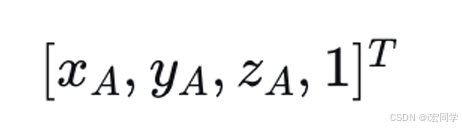
-
进行矩阵乘法运算
-
得到点在B下的齐次坐标,提取前三个分量即为直角坐标
(3)多个关节坐标系之间的变换,最后是如何得到末端相对基座的位姿的?