🎬 胖咕噜的稞达鸭 :个人主页
🔥 个人专栏 : 《数据结构》《C++初阶高阶》《算法入门》
⛺️技术的杠杆,撬动整个世界!


二叉树的概念
二叉树搜索树又叫二叉排序树,
左边的子树都是小于根,右边的子树都是大于根.
二叉搜索树的性能分析:
最优情况下,而成二叉搜索树为完全二叉树,(或者接近完全二叉树):其高度为O(log2N)
二叉搜索树的实现;
using可以展开命名空间,也可以用来定义类型,using Node=BSTNode<K> ,就是将Node作为BSTNode<K>的别名.
cpp
template<class K>
//定义结构
struct BSTNode
{
K _key;
BSTNode<K>* _left;
BSTNode<K>* _right;
BSTNode(const K& key)
:_key(key)
,_left(nullptr)
,_right(nullptr)
{ }
};
//用模板定义二叉搜索树的关键字,如果是大于关键字就往右边走,小于关键字就往左边走
template<class K>
class BSTree
{
//typedef BSTNode<K> Node;
using Node = BSTNode<K>;
public:
bool Insert(const K& key)
private:
Node* _root = nullptr;
};二叉树的插入
这里可以使用递归,也可以使用循环.假如说需要插入的数字小于根节点,往左边走,大于根节点,就往右边走,在可以使用递归和循环的时候,我们优先选择使用循环.
定义一个cur来记录判断过程,当cur<root,执行左边的操作,然后一直走到为空的地方New一个新的节点插入,右边也是这样的逻辑.但是在申请新的节点进行插入的时候,要跟二叉树有一个链接,所以我们定义一个parent节点,
当开始走的时候,parent指向空,cur指向root节点,Node* cur=_root,当root的左右子树不为空,判断cur->val小于key,就将cur=cur->right ,在此之前更新一下parent的节点,指向cur的位置,也就是parent=cur ;cur->val大于key,cur=cur->left ,在此之前更新一下parent的节点,指向cur的位置,也就是parent=cur .去重操作,将cur->val=key的情况返回false.也可以不去重,那就要将=的这种情况插入到>或<的判断中.
接着向下判断,走到空节点就结束循环.
此时cur走到空了,向上判断此时他的位置相比parent所在的值是大于还是小于,大于parent就向右插入到parent->right中,小于parent就插入到parent->left中.
最后返回true.
cpp
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_val < key)//如果此时cur所在的根节点的值小于要插入的key
{
parent = cur;//每次走的时候将值给parent
cur = cur->_right;
}
else if(cur->_val>key)
{
parent = cur;
cur = cur->_left;
}
else{ return false; }
}
cur = new node(key);
if (parent->_val < key) { parent->_right = cur; }
else { parent->_left = cur; }
return true;
}插入好了之后我们用中序遍历来打印出来,中序遍历就是先将左子树部分走完之后,打印出中间的根节点,再走右子树.
代码实现一下:
cpp
private:
void _Inorder(Node* root)
{
if(root==nullptr)
{
return;
}
_Inorder(root->_left);
cout<<root->_val<<" ";
_Inorder(root->_right);
}这里给一个案例数组用来测试,将数组中的数字插入到二叉搜索树中,最后用中序遍历打印出来;
注意:此时_root属于类中的私有成员,在类外面是不可以访问的,但是在类里面是可以的,所以这里我们在类中的公有部分public实现一个Inorder(),重新调用一下.;类里面二叉树的递归基本上都会用这种办法.
对二叉搜索树进行中序遍历,一定能够得到一个有序序列
cpp
public:
void Inorder()
{
_Inorder(_root);
}问题:为什么要在类的私有部分写_Inorder,在公有部分要调用Inorder,只有公有部分的才可以调用在类外面使用?那为什么不直接将_Inorder写在类公有部分:
这里是的面向对象设计中的封装性与接口设计的体现:
1.封装实现细节(隐藏私有办法):_Inorder是递归实现的内部细节,它需要接受Node* 类型的根节点参数才可以工作,如果直接暴露为公有接口,用户需要理解树的内部节点结构,甚至要处理nullptr的边界情况,这就违背了封装隐藏实现细节的原则。
把_Inorder放在私有部分,可以避免用户直接调用。
2.提供了简易的公有接口。
Inorder时对外提供的"遍历接口"调用方法可简单。
案例测试:
cpp
#include"BinaryTree.h"
int main()
{
BSTree<int> t;
int a[] = { 8,7,9,3,5,4,5,7,8,6,1,2 ,19};
for (auto e : a)
{
t.Insert(e);
}
t.Inorder();
}二叉搜索树的查找:
从根开始走,如果大于根就往右边查找,小于根就往左边查找;
最多查找高度次,如果走到空了还没有找到,那就说明这个值不存在.
如果不支持插入相等的值,找到即可返回.
如果没有去重,那么只需要找到位于中序的第一个x.
cpp
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_val > key) { cur = cur->_left; }
else if (cur->_val < key) { cur = cur->_right; }
else { return true; }
}
return false;
}二叉树的删除
这里就有难度的上升了,如果是叶子节点那就很好删了,删除叶子节点之后,为了防止父亲节点的叶子节点指向空位野指针,所以这里将删除的父亲节点的叶子节点置为空。
还有一种情况也是很好删除的,如果是只有一个子节点的父亲节点,删除之后让爷爷节点指向这个已删除的父亲节点的子节点。这样就完成了二叉树的连贯性。
这里再简练一点说明:"
1.要删除节点N左右孩子为空(删除叶子节点情况):把N节点的父亲节点对应孩子指针指向空,直接删除N节点;
2.1 要删除的节点N左孩子为空,右孩子不为空:把要删除节点N的父亲对应孩子指针指向N的右孩子,之直接删除N节点。2.2 要删除的节点N右孩子为空,左孩子不为空:把要删除节点N的父亲对应孩子指针指向N的左孩子,之直接删除N节点。
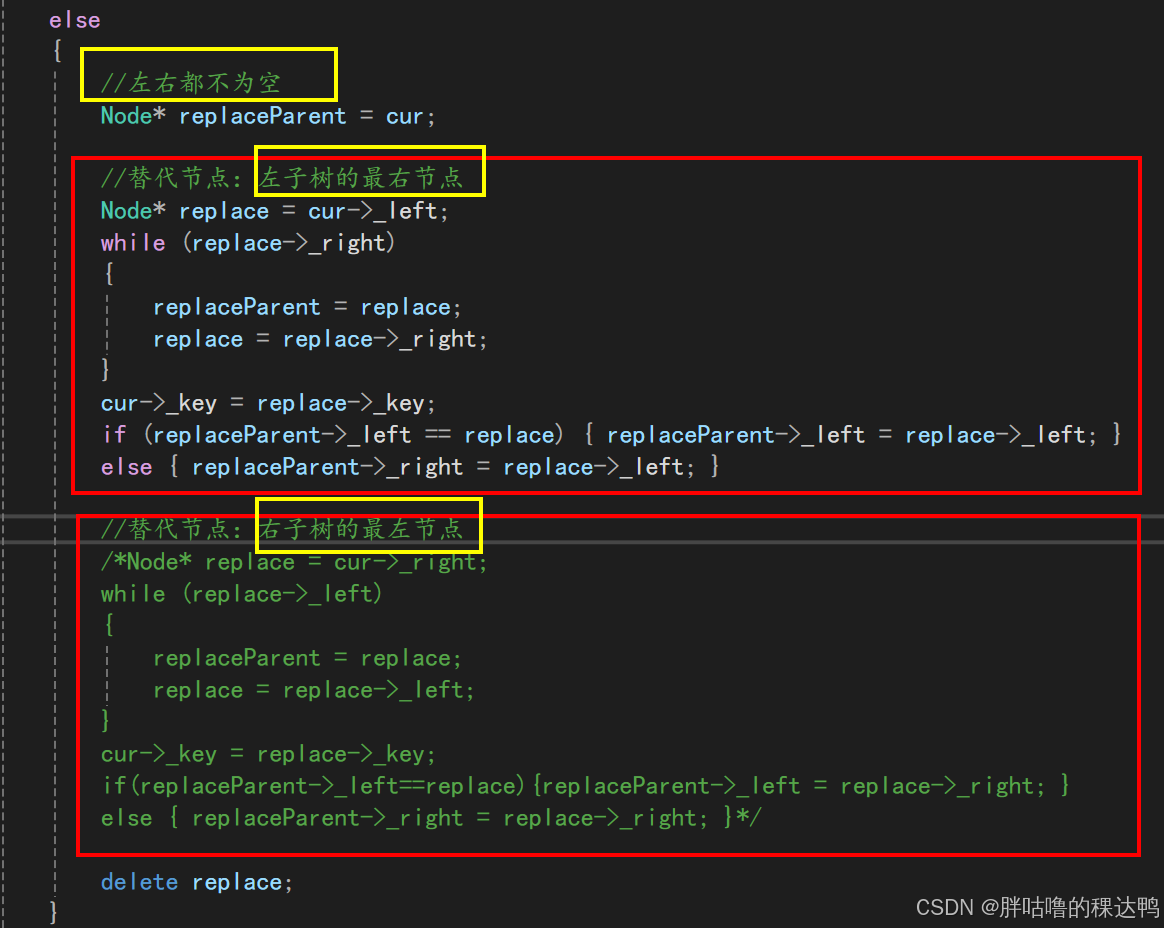
要删除的N节点左右孩子都不为空:这里就需要引入替代法,形象一点理解,如果一个父亲有很多个孩子,有一天父亲要出远门,所有的孩子都送到爷爷家,爷爷照顾不过来,这样就可以让家里一个最大的孩子来照顾,这种情况是右子树。所以,找N左子树的值最大节点R(最右节点)或者N右子树的最小节点R(最左节点)替代N,因为这两个节点中任意一个,放到N的位置都满足二叉搜索树的规则。
**
这里直接看图吧!!!强烈建议看图理解!
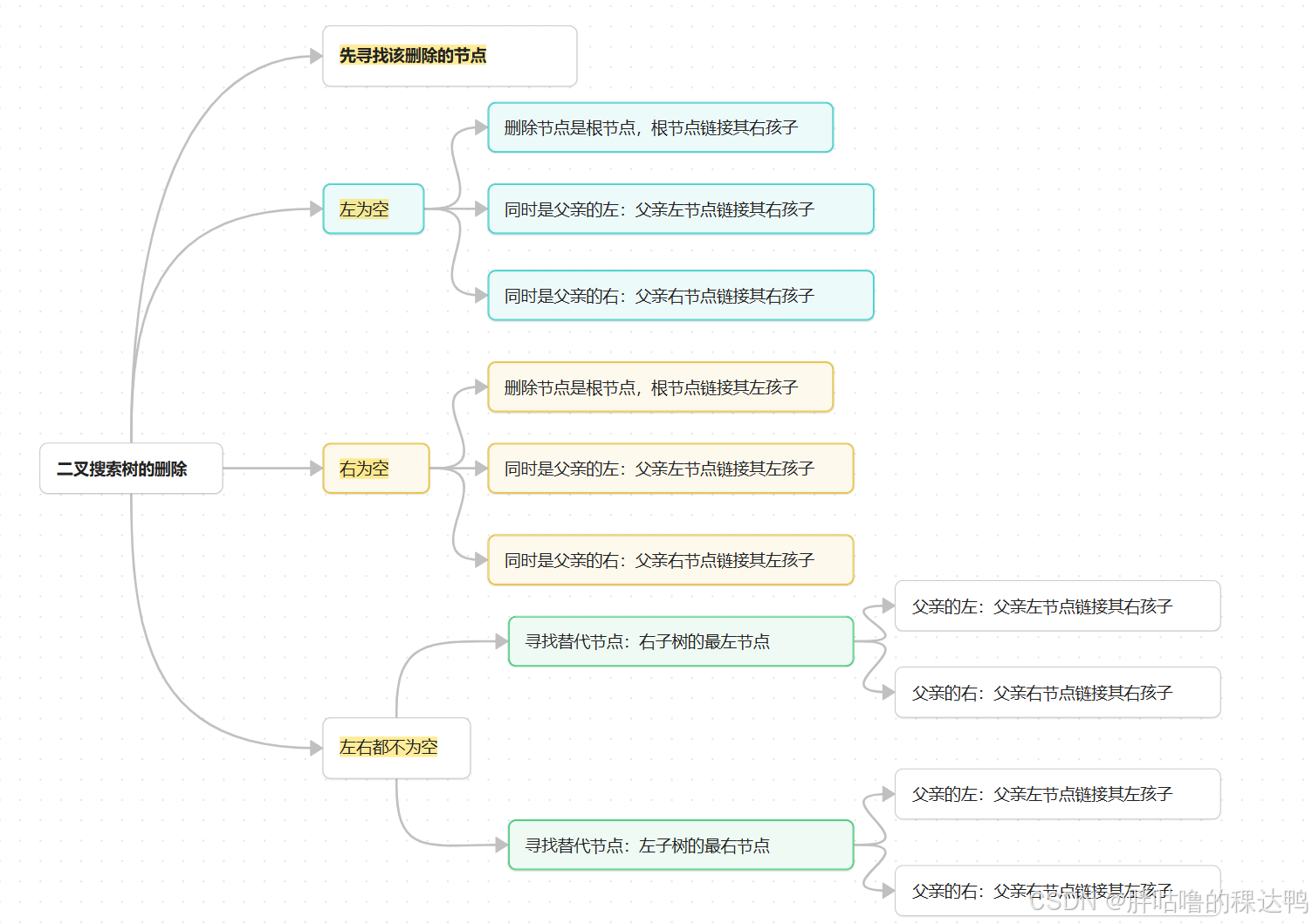
**
写一个大致的框架:
cpp
bool Erase(const K& key)
{
Node* cur=_root;
while(cur)
{
if(cur->val>key){parent=cur;cur=cur->left;}
else if(cur->val<key){parent=cur;cur=cur->right;}
else{
//删除
//左为空
if(cur->_left==nullptr)
{}
//右为空
else if(cur->_right==nullptr)
{}
else
{//左右都不为空
}
}
}
return false;
}删除的时候要分为三种情况。
- 左为空
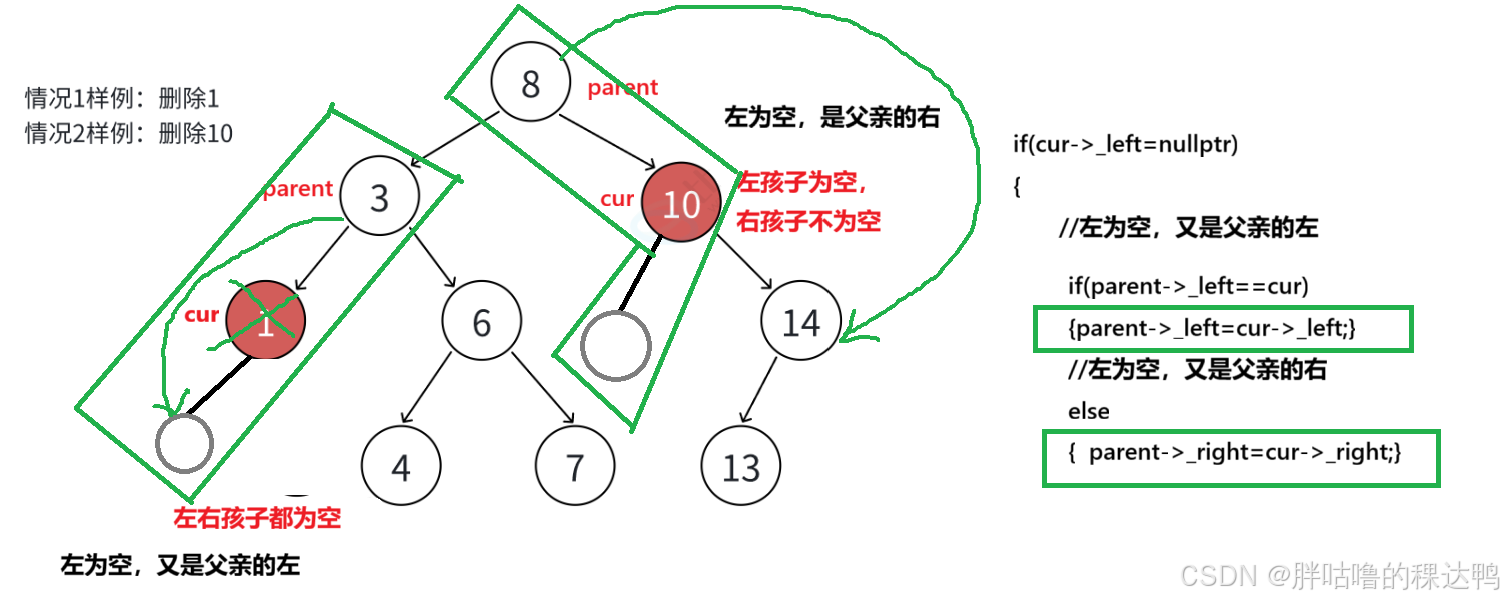
cpp
//左为空
if(cur->_left == nullptr)
{
if (cur == _root) { _root = cur->_right; }
else
{
if (parent->_left == cur)//左为空,又是父亲的左
{
parent->_left = cur->_right;
}
else//左为空,但是又是父亲的右
{
parent->_right = cur->_right;
}
}
delete cur;
}- 右为空
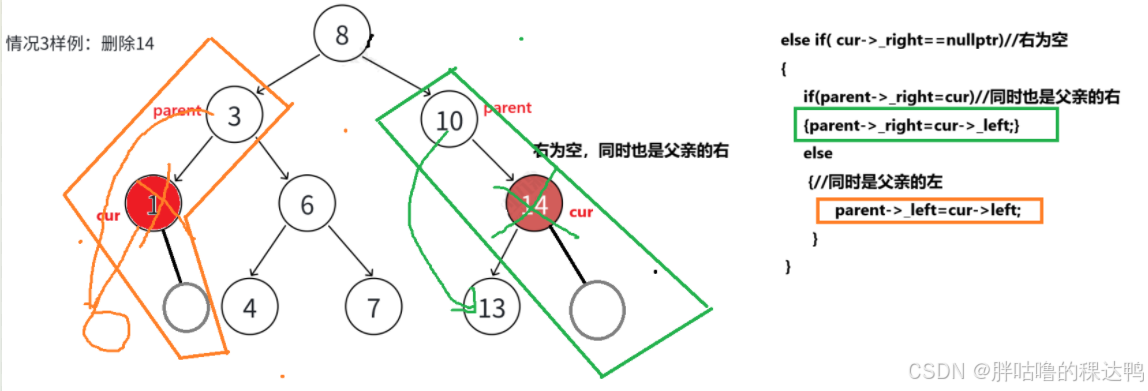
cpp
//右为空
else if (cur->_right == nullptr)
{
if (cur == _root) { _root = cur->_left; }
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else { parent->_right = cur->_left; }
}
delete cur;//删除掉cur元素
}注意!!!还有一种情况:假如是删除根节点:此时也可以分别插入到上面的情况:
根节点的左边为空,右边不为空,也即是cur==_root;则将cur的右赋值给_root;_root=cur->_right;
根节点的右边为空,左边不为空,也即是cur==_root,则将cur的左赋值给_root;_root=cur->_left;
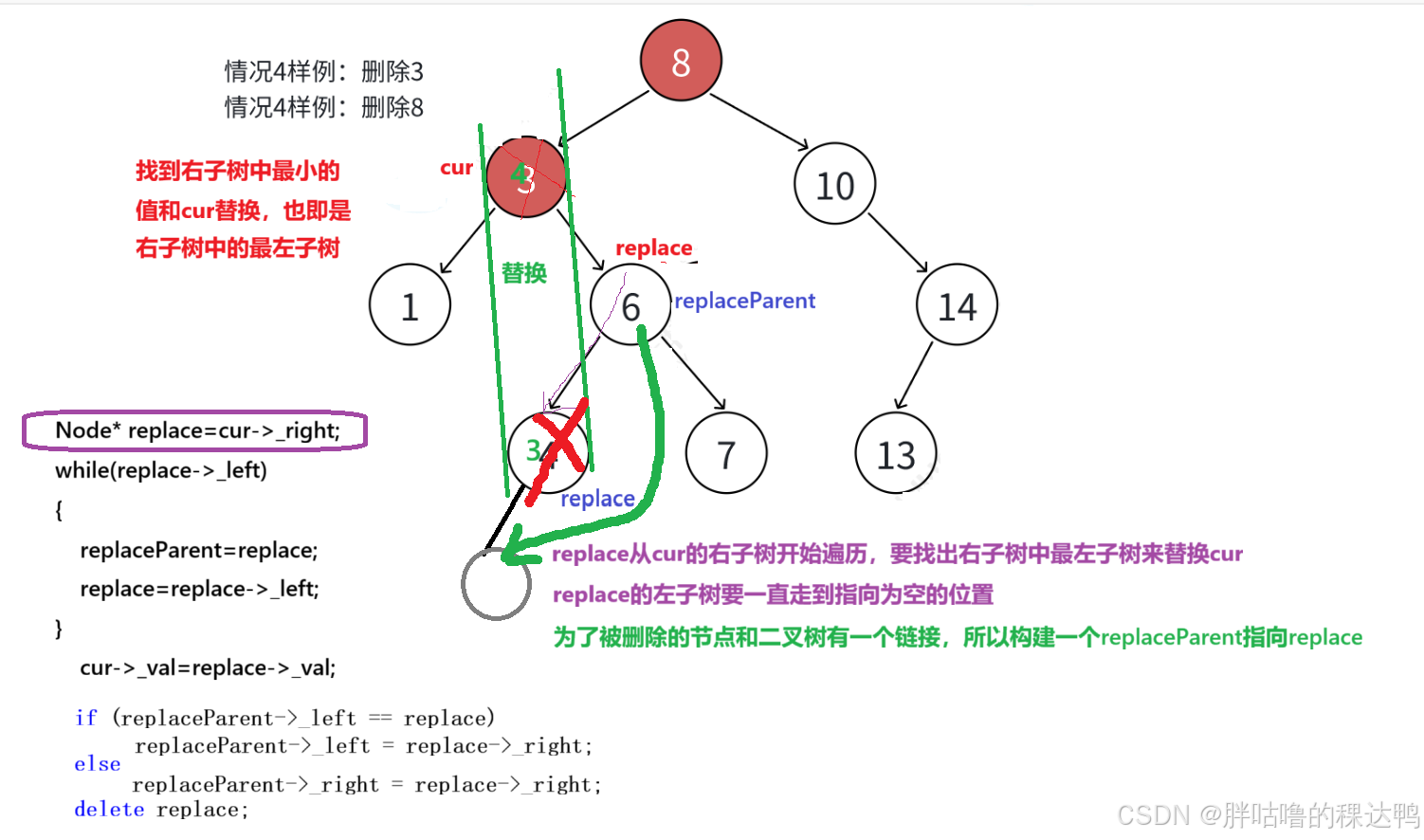
- 左右都不为空
左右都不为空,此时需要替代,用右子树的最小节点或者是左子树的最大节点替代都不违反二叉搜索树的特性即可
cpp
else
{//左右都不为空,此时需要替代,用右子树的最左节点或者是左子树的最右节点替代都不违反二叉搜索树的特性即可
Node* replaceParent = cur;
Node* replace = cur->_right;
while (replace->_left)
{
replaceParent = replace;
replace = replace->_left;
}
cur->_val=replace->_val;//不可以交换位置,就是将replace的值赋值给cur,此时完成了交换
if (replaceParent->_left == replace)
replaceParent->_left = replace->_right;
else
replaceParent->_right = replace->_right;
delete replace;
}
搜索二叉树的修改:
普通搜素二叉树不可以被修改。否则会破坏性质。
二叉搜索树源码:
cpp
#pragma once
#include<iostream>
using namespace std;
namespace Key
{
template <class K>
struct MyBSTNode
{
K _key;
MyBSTNode<K>* _left;
MyBSTNode<K>* _right;
MyBSTNode(const K& key)
:_key(key)
,_left(nullptr)
,_right(nullptr)
{ }
};
template<class K>
class MyBSTree
{
using Node = MyBSTNode<K>;
public:
bool Insert(const K& key)
{
if (_root == nullptr) { _root = new Node(key); return true; }
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < key) { parent = cur; cur = cur->_right; }
else if (cur->_key > key) { parent = cur; cur = cur->_left; }
else { return false; }
}
cur = new Node(key);
if (parent->_key < key) {parent->_right=cur; }
else { parent->_left = cur; }
return true;
}
bool find(const K& key)
{
Node* cur = _root;
while(cur)
{
if (cur->_key > key) { cur = cur->_left; }
else if(cur->_key<key){ cur = cur->_right; }
else { return true; }
}
return false;
}
bool Erase(const K& key)
{
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key > key) { parent = cur; cur = cur->_left; }
else if (cur->_key < key) { parent = cur; cur = cur->_right; }
else
{
if (cur->_left == nullptr)//左为空
{
if (cur == _root) { _root = cur->_right; }
else
{
if (parent->_left == cur) { parent->_left = cur->_right; }
else { parent->_right = cur->_right; }
}
delete cur;
}
else if (cur->_right == nullptr)//右为空
{
if (cur == _root) { _root = cur->_left; }
else
{
if (parent->_left == cur) { parent->_left = cur->_left; }
else { parent->_right = cur->_left; }
}
delete cur;
}
else
{
//左右都不为空
Node* replaceParent = cur;
//替代节点:左子树的最右节点
Node* replace = cur->_left;
while (replace->_right)
{
replaceParent = replace;
replace = replace->_right;
}
cur->_key = replace->_key;
if (replaceParent->_left == replace) { replaceParent->_left = replace->_left; }
else { replaceParent->_right = replace->_left; }
//替代节点:右子树的最左节点
/*Node* replace = cur->_right;
while (replace->_left)
{
replaceParent = replace;
replace = replace->_left;
}
cur->_key = replace->_key;
if(replaceParent->_left==replace){replaceParent->_left = replace->_right; }
else { replaceParent->_right = replace->_right; }*/
delete replace;
}
return true;
}
}
return false;
}
void Inorder()
{
_Inorder(_root);
cout << endl;
}
private:
void _Inorder(Node* root)
{
if (root == nullptr)
{
return;
}
_Inorder(root->_left);
cout << root->_key << " ";
_Inorder(root->_right);
}
private:
Node* _root = nullptr;
};
}测试:
cpp
#define _CRT_SECURE_NO_WARNINGS 1
#include"BinaryTree.h"
int main()
{
Key::MyBSTree<int>t;
int a[] = { 8,7,9,3,5,4,5,7,8,6,1,2 ,19,99 };
for (auto e : a)
{
t.Insert(e);
}
t.Inorder();
t.Erase(19);
t.Inorder();
}二叉树搜索树的应用:
小区停车,会检查车牌号,在本小区里面的车,会登记车牌号录入后台系统,非本小区的车想要进去,就会显示"非本小区车辆"
检查一篇文章中的英文字母有没有拼写错误,将词库中所有单词都放入二叉搜索树,读取文章的单词,查找是否在二叉搜索树中,不在波浪线中则标红提示。
key/value搜索场景:
每一个关键码key都有一个对应的值
value,value可以是任意类型的对象,树的节点中除了存储key还要存储对应的value,增删查还是以Key为关键字走二叉搜索树的规则进行比较,可以快速的查找到key对应的value,key/value的搜索树支持修改,但是不支持修改key,修改key就会破坏搜索树的结构,可以修改value.
场景1:简单中英互译字典:树的结构中(节点)存储key(英文)和value(中文),搜索时输入英文,则同时会查找到中文。
场景2:商场车库:入库时扫描车牌,记录车牌和入场时间,出口离开,扫描车牌,查找 入场时间,用当前时间---入场时间计算出停车时间长,计费让车离开。
KV搜索树的析构:
cpp
private:
void Destroy(Node* root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
cpp
public:
~MyBSTree()
{
Destroy(_root);
_root=nullptr;
}KV搜索树的拷贝:(用前序遍历拷贝这棵树的节点)
cpp
private:
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newRoot = new Node(root->_key, root->_value);
newRoot->_left = Copy(root->_left);
newRoot->_right = Copy(root->_right);
return newRoot;
}
cpp
public:
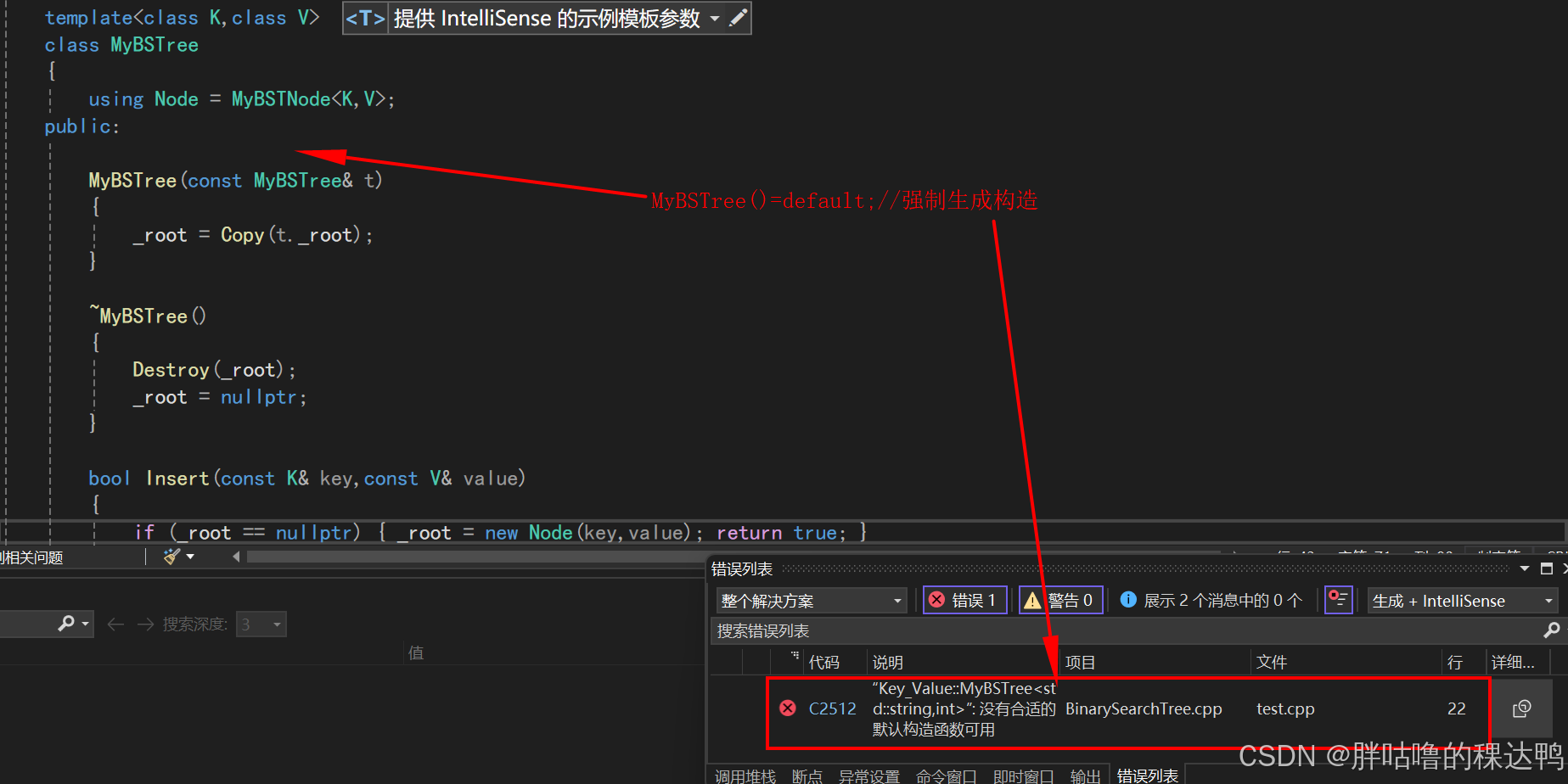
MyBSTree()=default;
MyBSTree(const MyBSTree& t)
{
_root = Copy(t._root);
}这里会有如下的报错,加上MyBSTree()=default;强制生成构造即可。
赋值:
cpp
public:
MyBSTree& operator=(MyBSTree tmp)
{
swap(_root, tmp._root);
return *this;
}KV二叉搜索树源码实现:
cpp
#include<iostream>
using namespace std;
namespace Key_Value
{
template <class K,class V>
struct MyBSTNode
{
K _key;
V _value;
MyBSTNode<K,V>* _left;
MyBSTNode<K,V>* _right;
MyBSTNode(const K& key,const V& value)
:_key(key)
,_value(value)
,_left(nullptr)
,_right(nullptr)
{ }
};
template<class K,class V>
class MyBSTree
{
using Node = MyBSTNode<K,V>;
public:
MyBSTree() = default;
MyBSTree(const MyBSTree& t)
{
_root = Copy(t._root);
}
~MyBSTree()
{
Destroy(_root);
_root = nullptr;
}
MyBSTree& operator=(MyBSTree tmp)
{
swap(_root, tmp._root);
return *this;
}
bool Insert(const K& key,const V& value)
{
if (_root == nullptr) { _root = new Node(key,value); return true; }
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < key) { parent = cur; cur = cur->_right; }
else if (cur->_key > key) { parent = cur; cur = cur->_left; }
else { return false; }
}
cur = new Node(key,value);
if (parent->_key < key) {parent->_right=cur; }
else { parent->_left = cur; }
return true;
}
Node* find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key > key) { cur = cur->_left; }
else if(cur->_key<key){ cur = cur->_right; }
else { return cur; }
}
return nullptr;
}
bool Erase(const K& key)
{
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key > key) { parent = cur; cur = cur->_left; }
else if (cur->_key < key) { parent = cur; cur = cur->_right; }
else
{
if (cur->_left == nullptr)//左为空
{
if (cur == _root) { _root = cur->_right; }
else
{
if (parent->_left == cur) { parent->_left = cur->_right; }
else { parent->_right = cur->_right; }
}
delete cur;
}
else if (cur->_right == nullptr)//右为空
{
if (cur == _root) { _root = cur->_left; }
else
{
if (parent->_left == cur) { parent->_left = cur->_left; }
else { parent->_right = cur->_left; }
}
delete cur;
}
else
{
//左右都不为空
Node* replaceParent = cur;
//替代节点:左子树的最右节点
/*Node* replace = cur->_left;
while (replace->_right)
{
replaceParent = replace;
replace = replace->_right;
}
cur->_key = replace->_key;
if (replaceParent->_left == replace) { replaceParent->_left = replace->_left; }
else { replaceParent->_right = replace->_left; }*/
//替代节点:右子树的最左节点
Node* replace = cur->_right;
while (replace->_left)
{
replaceParent = replace;
replace = replace->_left;
}
cur->_key = replace->_key;
if(replaceParent->_left==replace){replaceParent->_left = replace->_right; }
else { replaceParent->_right = replace->_right; }
delete replace;
}
return true;
}
}
return false;
}
void Inorder()
{
_Inorder(_root);
cout << endl;
}
private:
void Destroy(Node* root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newRoot = new Node(root->_key, root->_value);
newRoot->_left = Copy(root->_left);
newRoot->_right = Copy(root->_right);
return newRoot;
}
void _Inorder(Node* root)
{
if (root == nullptr)
{
return;
}
_Inorder(root->_left);
cout << root->_key << " :" << root->_value << endl;
_Inorder(root->_right);
}
private:
Node* _root = nullptr;
};
}
cpp
#define _CRT_SECURE_NO_WARNINGS 1
#include"BinaryTree.h"
//int main()
//{
// Key::MyBSTree<int>t;
// int a[] = { 8,7,9,3,5,4,5,7,8,6,1,2 ,19,99 };
// for (auto e : a)
// {
// t.Insert(e);
// }
// t.Inorder();
//
// t.Erase(4);
// t.Inorder();
//}
int main()
{
string arr[] = {"冬","春","冬", "春","夏" };
Key_Value::MyBSTree<string, int>countTree;
for (const auto& str : arr)
{
auto ret = countTree.find(str);
if (ret == nullptr)
{
countTree.Insert(str, 1);
}
else
{
//修改value
ret->_value++;
}
}
countTree.Inorder();
return 0;
}