引言:
先前我们讲解完了顺序表相关知识,包括顺序表的创建、初始化、插入、删除、查找等功能的实现,接下来本节内容就让我们动手练习一下顺序表相关的题目,加深一下理解。
文章目录
[一、移除元素 - 力扣(LeetCode)](#一、移除元素 - 力扣(LeetCode))
[二、删除有序数组中的重复项 - 力扣(LeetCode)](#二、删除有序数组中的重复项 - 力扣(LeetCode))
[三、合并两个有序数组 - 力扣(LeetCode)](#三、合并两个有序数组 - 力扣(LeetCode))
一、移除元素 - 力扣(LeetCode)


我们来看一下第1题的题目要求:需要原地移除值为val的数,并返回不等与val的元素个数k,再通过示例加强理解:我们有一个nums数组,要移除的val值等于3,那就要把数组中的3全部移除,然后还剩下2个2要放在最右边,最后函数返回剩余元素的个数k=2。
cpp
int removeElement(int* nums, int numsSize, int val) {
}接着我们看题目给出的已知函数的外壳长什么样,这是一个叫做removeElenment的函数,需要3个参数,数组地址nums,有效元素个数nameSize,要移除的值val,最后函数还要返回一个int整型,也就是我们的k。
1.1思路1:创建新数组
我们现在要对数组进行操作,第一感觉可能是在原数组中直接删除值不好删除,那我们能不能再创建一个新数组呢?遇到不等于val的值就放入新数组中,最后再将新数组赋值给旧数组。这就是我们的第1个思路,代码如下:
cpp
// 方法1:创建新数组
int removeElement(int* nums, int numsSize, int val) {
int* copy_nums = (int*)malloc(numsSize * sizeof(int));
int k = 0;
//插入到新数组中
for (int i = 0; i < numsSize; i++)
{
if (nums[i] == val)
{
continue;//如果相等则跳过当前循环
}
copy_nums[k++] = nums[i];
}
//赋值给原数组
for (int i = 0; i < k; i++)
{
nums[i] = copy_nums[i];
}
return k;
}我们使用了malloc开辟了numsSize * sizeof(int)大小的空间,然后进入for循环,对于等于val的值我们跳过当前循环,不等于val的值赋值到新数组copy_nums中,最后在用for循环将新数组赋值给旧数组,同时返回k值。
我们现在已经学完了复杂度的相关概念,自然在写代码的时候就需要考虑我们的算法复杂度如何,我们现在这个创建新数组思路的空间复杂度自然为O(n)因为malloc开辟了numsSize大小的空间,而时间复杂度呢?有2个并列的for循环,所以时间复杂度也为O(n),那还有更加优秀的思路吗?有的兄弟,有的,就是接下来我们要讲的双指针法。
1.2思路2:双指针法
双指针法是指创建2个变量dst,src,如果src指向的数据是val,则src++,如果src指向的数据不是val,赋值(src给dst),src和dst都++。
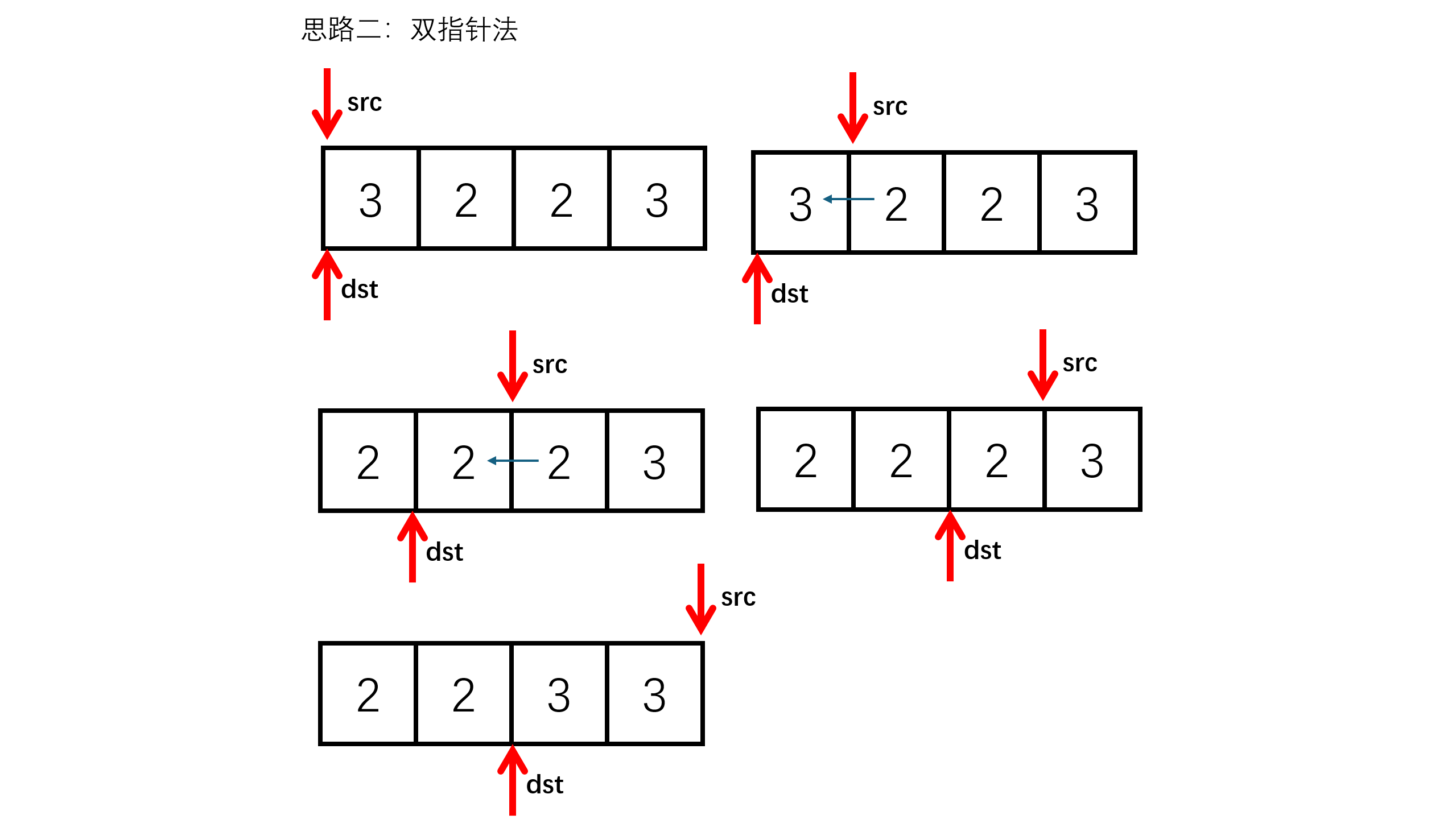
这里dst和src初始都指向3,现在判断3是否为val,是则src++,因为我们是需要找的是不等于val的值,然后把它放在前面,接下来src指向2不等于val,则将src的值赋给dst,然后sre和dst都++,如此循环往复,直到src指向空。代码实现如下:
cpp
int removeElement(int* nums, int numsSize, int val) {
int src = 0;
int dst = 0;
while (src < numsSize)
{
if (nums[src] != val)
{
nums[dst] = nums[src];
dst++;
}
src++;
}
return dst;
}我们再判断一下这里的复杂度问题,该思路没用额外开辟空间,所以空间复杂度为O(1),只有一个while循环,所以时间复杂度为O(N),所以该思路是要优于上一种创建新数组方法的。
二、删除有序数组中的重复项 - 力扣(LeetCode)


我们来看题目要求,给了一个非严格递增排列的数组nums,啥意思,我们看示例1,nums = [1,1,2]就是说数组中的值整体来说是递增的,但是可以包含重复的值,然后要求我们删除重复的值之后使元素的相对顺序保持一致,也就是说还是维持递增排列,最后返回不重复元素的个数k。
2.1思路1:创建新数组
创建新数组,遍历原数组,将不重复数据导入到新数组中,然后将新数组赋给原数组。这里和之前不一样的一点就是我们要找不重复的数据,所以如果我们只用一个变量去遍历是不够的,因此创建2个变量,一个记录值,一个找是否存在与记录值相同的值,将不重复的值放到新数组中。
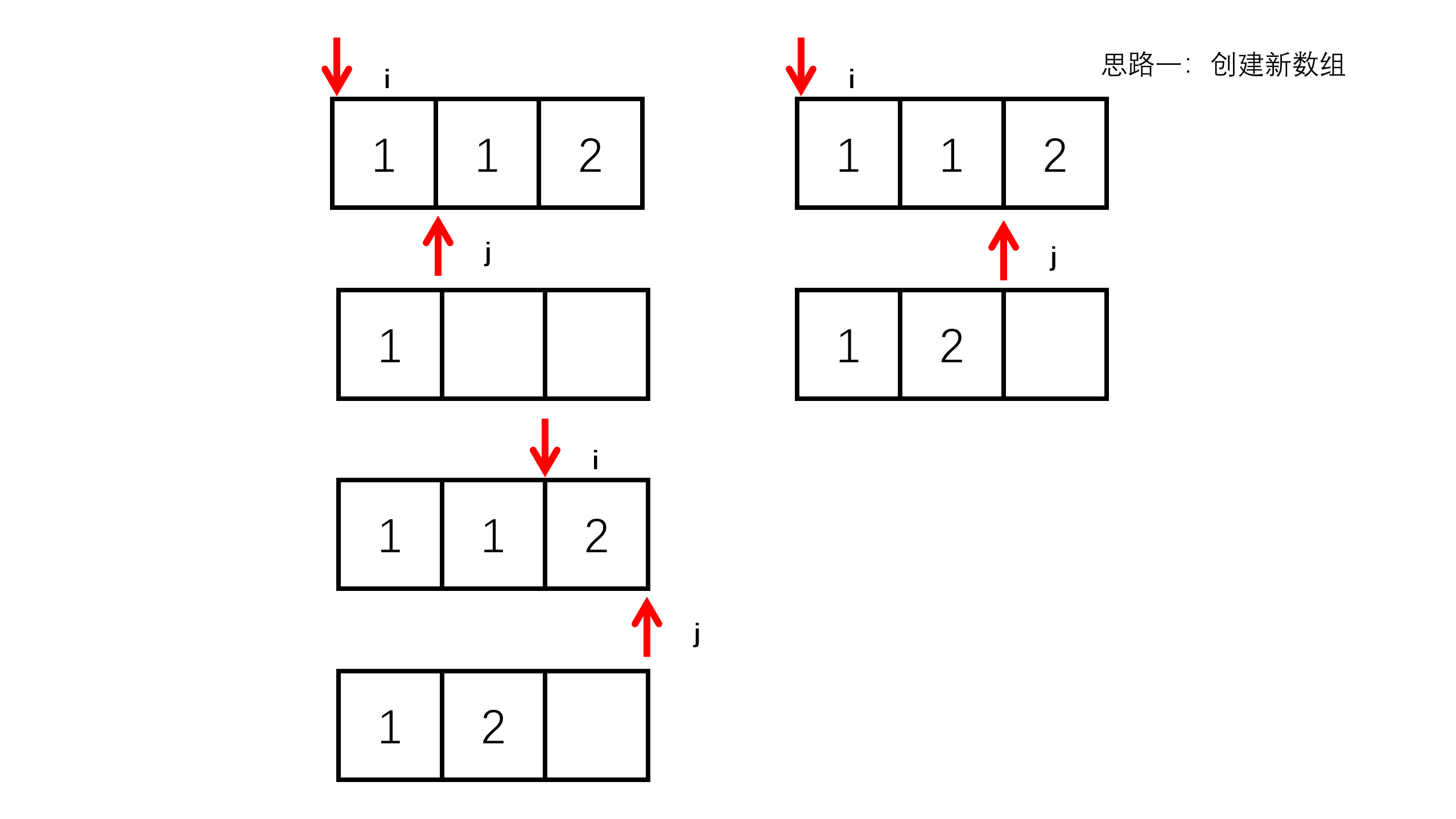
我们创建了i和j2个变量,初始 i 等于0, j 等于i + 1,如果 j 等于 i 的值,则 j 继续++,直到找到不等于 i 的值,然后放入新数组中,接着 i 来到 j 的位置,j++,如此循环如上操作,直到 j 指向空,跳出循环。代码如下:
cpp
// 思路1:创建新数组
int removeDuplicates(int* nums, int numsSize) {
int* copy_nums = (int*)calloc(numsSize , sizeof(int));
int i = 0;
int j = i + 1;
int k = 1;//因为i = 0是已经放入新数组中,因此新数组下标从k = 1开始
copy_nums[i] = nums[i];
while (j < numsSize)
{
if (nums[j] != nums[i])
{
copy_nums[k] = nums[j];
k++;
i = j;
}
j++;
}
for (i = 0; i < numsSize; i++)
{
nums[i] = copy_nums[i];
}
return k;
}该方法还是时间复杂度和空间复杂度都为O(N),那我们再试试思路2:双指针法,其实第1种创建新数组方法中已经用到了一点双指针的东西,我们在这个基础上改改就可以得到双指针法。
2.2思路2:双指针法
双指针法,创建2个变量,变量dst指向初始位置,变量src指向dst + 1的位置,如果src的值等于dst的值,则src++,如果src的值不等于dst的值,则先让dst++,再将src的值赋给dst,接着src++,如此循环往复直至src指向空。
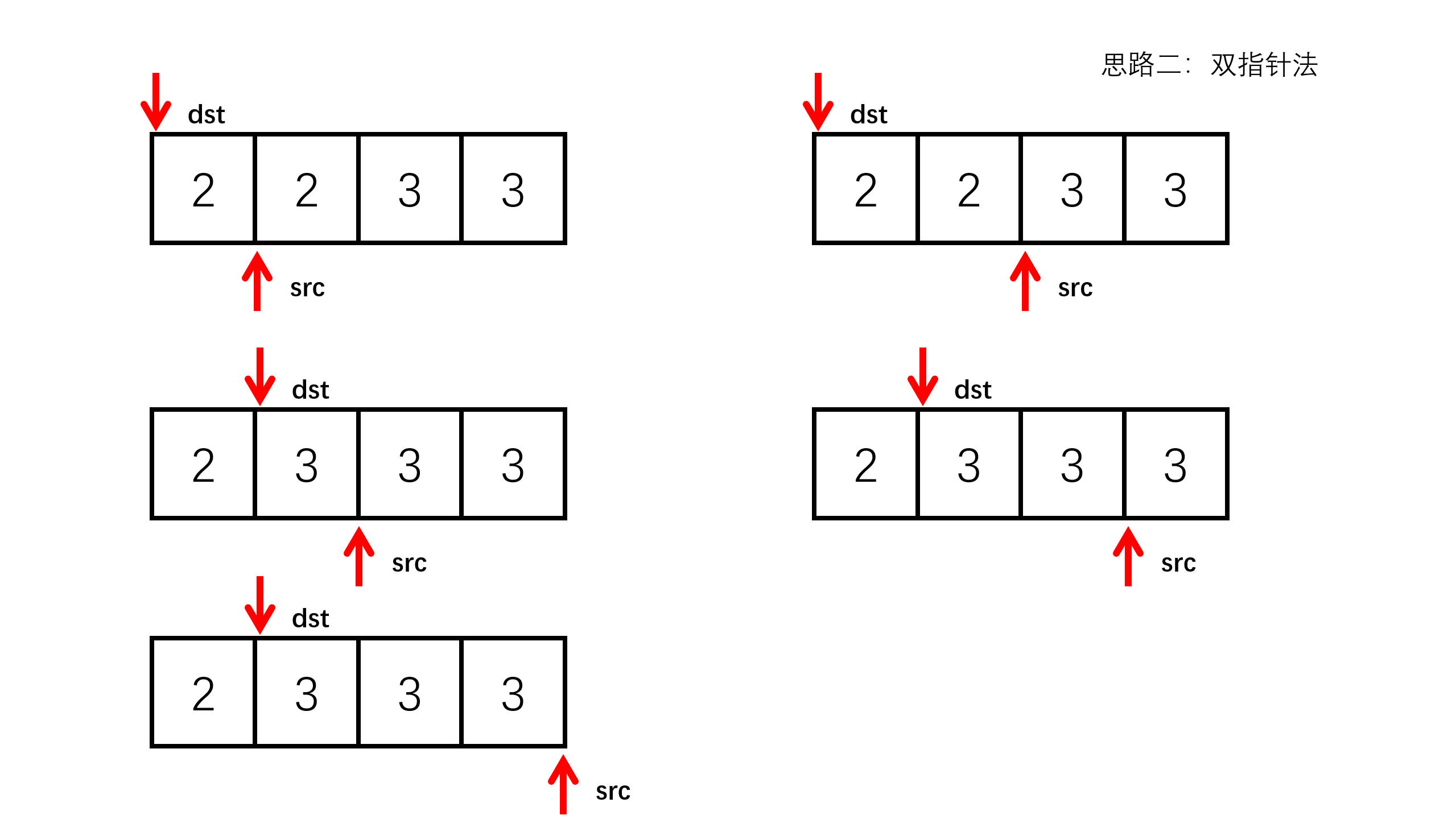
这里我们让dst初始指向0,则src初始指向1,这时dst的值和src的值都为2,则src++向后移动一位,src的值变成了3,先让dst++向后移动一位,再将src的3赋给了dst,然后src++指向了3等于dst的值,接着src++指向了空,循环结束,最后返回不重复元素的个数为dst + 1。代码实现如下:
cpp
int removeDuplicates(int* nums, int numsSize) {
int dst = 0;
int src = dst + 1;
while (src < numsSize)
{
if (nums[src] != nums[dst])
{
dst++;
nums[dst] = nums[src];
}
src++;
}
return dst + 1;
}这里还有一个可以优化的地方,假如我们的数组为:[2,3,4,4],我们的det初始指向2,src指向3,这时候,src和dst不相等,需要先dst++再赋值,但是我们可以看到,dst++之后和src指向同一个值,这样再交换就重复了,因此这里可以优化为只有不相等时才交换。
cpp
// 思路2:双指针法
int removeDuplicates(int* nums, int numsSize) {
int dst = 0;
int src = dst + 1;
while (src < numsSize)
{
if (nums[src] != nums[dst])
{
dst++;
if(src != dst)
nums[dst] = nums[src];
}
src++;
}
return dst + 1;
}三、合并两个有序数组 - 力扣(LeetCode)


读完题目要求我们可以知道的是,要求我们合并2个升序的数组,将nums2放在nums1中,同时让nums1也为升序。有一个最简单是思路就是先不管其他的,直接将nums2中的元素全部插入到nums1中,再对nums1进行排序就行,排序算法选择冒泡排序或者qsort排序都行。我们这里讲第2种思路,比较大小,依次将nums2中的元素根据大小插入到nums1中。
比如示例1,我们先拿num2中的2和nums1中的元素比较,遍历nums1,如果我们将num2中的2插入到1的后面,那是不是num1中的2,3都要往后移动,这样的从前往后遍历,谁小谁往前放就非常麻烦,我们可以换一下方向,可以从后往前遍历,谁大谁往后放。
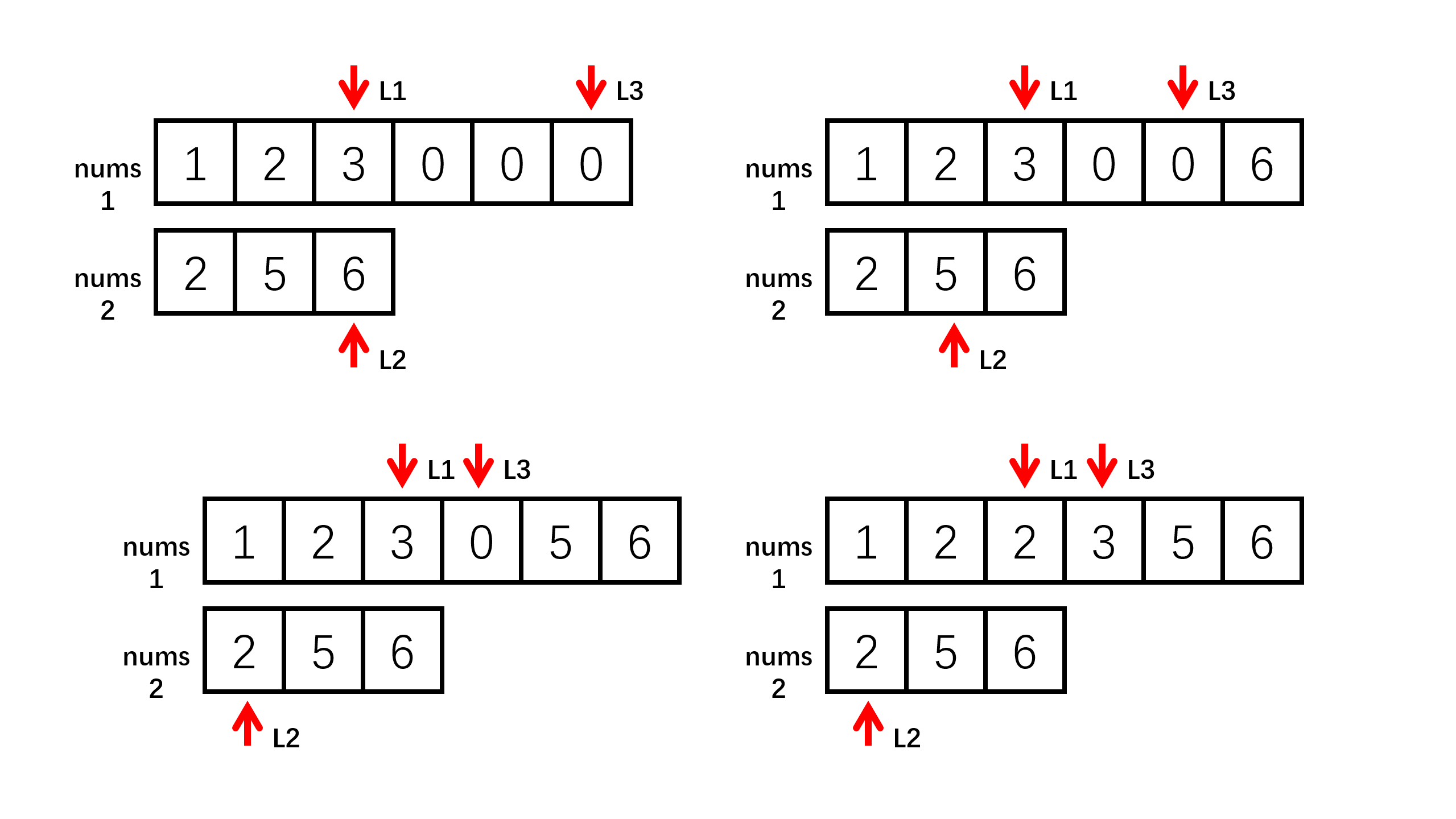
这里我们定义了3个变量,一个L1指向要插入数组nums1中有效元素中最后的一个,一个L2指向插入数据来源nums2中的最后一个元素,一个L3指向nums1最后的位置,即开始插入的位置。初始我们比较nums1中最大的数和nums2中最大的数,二者中最大的数放在L3的位置。例如初始L1为3,L2为6,所以6就放在L3的位置,然后L3--,L2--,L1不变,接着继续比较L1和L2的值,L1为3,L2为5,所以5就放在L3的位置,然后L3--,L2--,L1不变,接着L1为3,L2为2,所以3放在L3的位置,L3--,L1--,L2不变,接着L1为2,L2为2,所以2放在L3的位置,L2--指向空就跳出循环。
这里是L2先越界,那么有没有可能L1先越界呢,我们给出2个新数组。
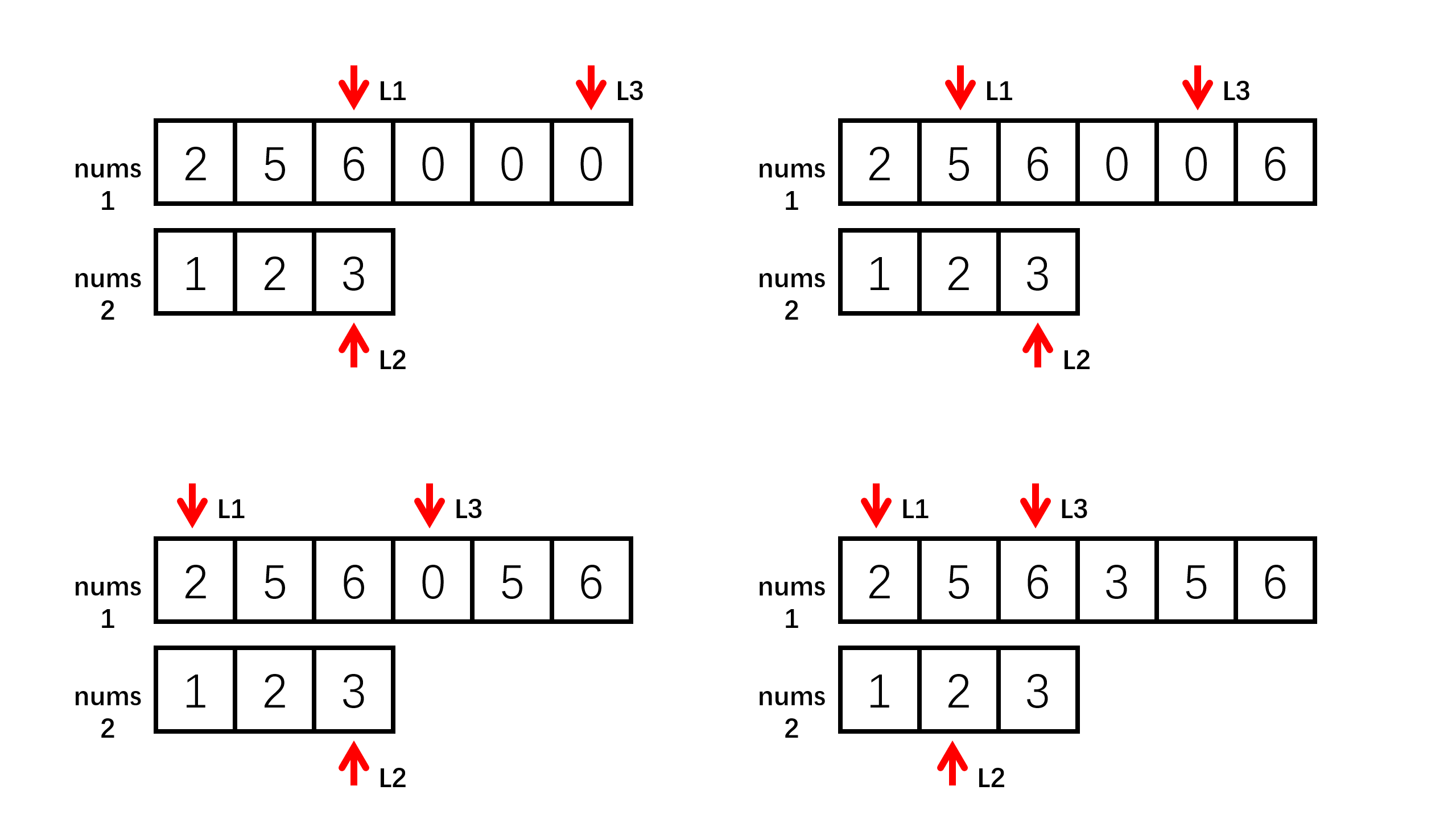
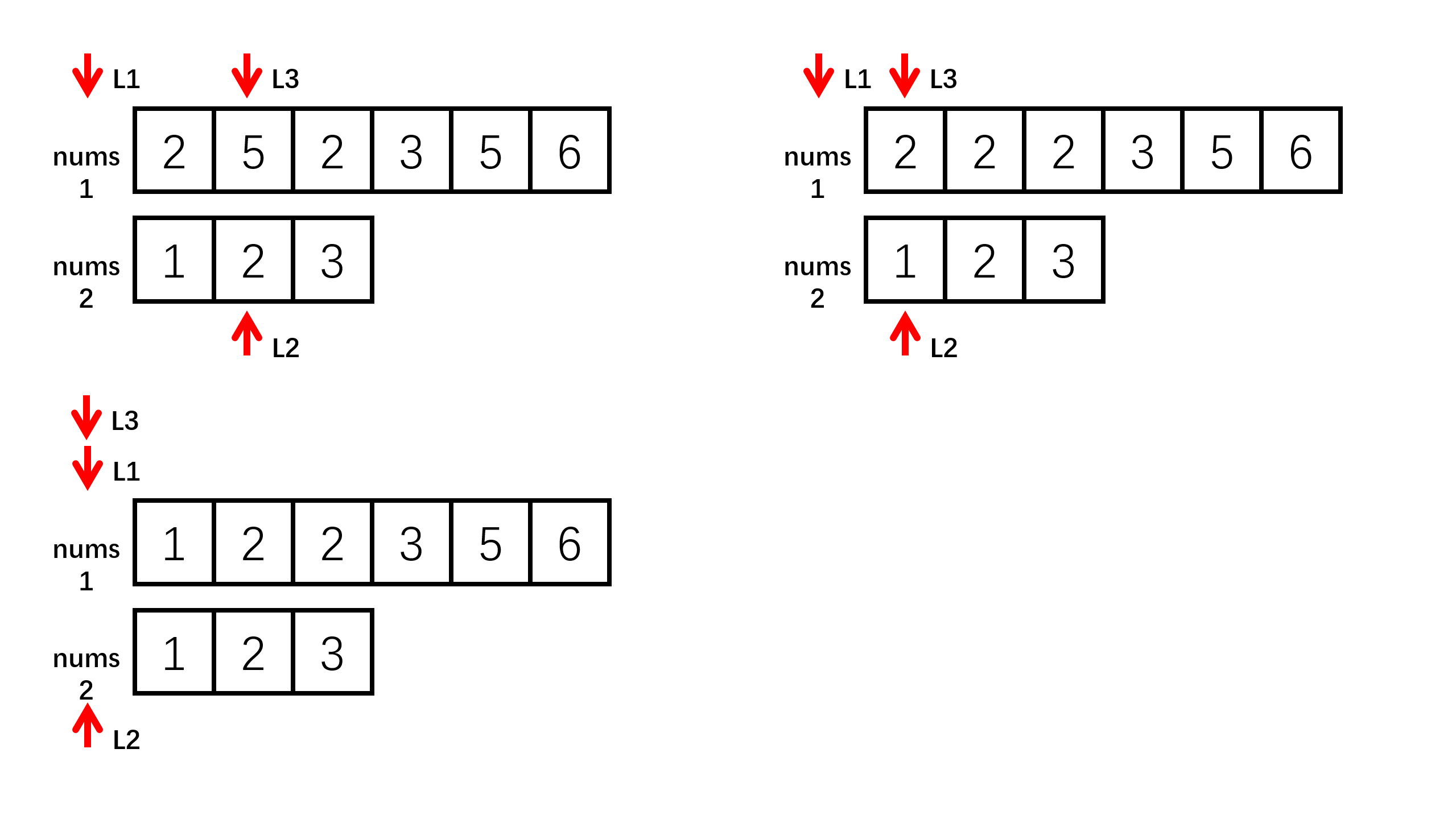
这里L1初始为6,L2为3,所以6放入L3的位置,L3--,L1--,L2不变,接着L1为5,L2为3,所以5放入L3的位置,L3--,L1--,L2不变,接着L1为2,L2为3,所以3放入L3的位置,L3--,L2--,L1不变,接着L1为2,L2为2,假设L1大,填入L3的位置,则L3--,L1--,L2不变,这时L1就越界了。现在我们发现nums2中还有1,2没放入nums1中,该怎么办,应该直接将1,2循环放入L1的前2个位置,因为我们可以知道L3之后的数据一定时比现在L2中的数据大的,所以可以直接从前放入。代码实现如下:
cpp
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {
int L1 = m - 1;
int L2 = n - 1;
int L3 = m + n - 1;
while (L1 >= 0 && L2 >= 0)
{
if (nums1[L1] > nums2[L2])
{
nums1[L3--] = nums1[L1--];
}
else
{
nums1[L3--] = nums2[L2--];
}
}
//L1越界
while (L2 >= 0)
{
nums1[L3--] = nums2[L2--];
}
//L2越界(不需要处理)
//L1、L2同时越界(不存在)
}该思路的时间复杂度为O(N),空间复杂度为O(1)。
好了,我们顺序表的习题就讲到这里,下次我们将进入单链表的学习,尽情期待。