
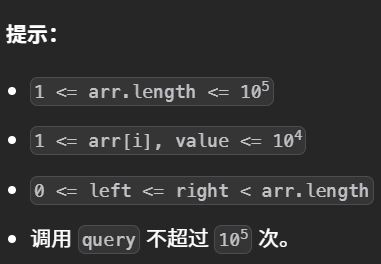
这一题的大意是让我们寻找在一个数组中的某一子数组中某一个元素出现的次数。
找一个元素在某一数组中出现的次数,我们通常会想到的是遍历一遍数组用哈希表来统计该元素出现的次数,但问题是这道题中会有最多10^5次询问,而数组的长度最多为 10 ^5,暴力遍历肯定是超时的,这时候我们可以采用二分的形式,通过找该元素最早出现的位置和该元素最晚出现的位置,两者相减就是出现的次数,时间复杂度O(nlogn)可以接受
但是要注意的是虽然使用二分可以下降到O(logn)但是二分需要在单调区间中才能使用,而题目中给出的序列是无序的,我们如果在每一次进行二分前进行一个排序的话,那么时间复杂度会超时,O(n)*(nlogn)(排序的时间复杂度 * n次询问)。
我之前写的就是排序+二分的做法超时了:
cpp
class RangeFreqQuery {
public:
vector<int> a;
RangeFreqQuery(vector<int>& arr) {
for(int i=0;i<arr.size();i++)
{
a.push_back(arr[i]);
}
}
int query(int left, int right, int value) {
//排序
vector<int> temp=a;
sort(temp.begin()+left,temp.begin()+right+1);
int l=left;
int r=right;
//找第一个大于等于value的位置
//找第一个小于等于value的位置
//如果数组中有value 那么
// 那么这两个位置都一定在value上
int lx=INT_MAX;
while(l<=r)
{
int mid=(l+r)/2;
if(temp[mid]==value)
{
r=mid-1;
lx=min(lx,mid);
}
else if(temp[mid]>value)
{
r=mid-1;
}
else{
l=mid+1;
}
}
//找到最左端的lx value
int rx=-1;
l=left;
r=right;
while(l<=r)
{
int mid=(l+r)/2;
if(temp[mid]==value)
{
l=mid+1;
rx=max(rx,mid);
}
else if(temp[mid]>value){
r=mid-1;
}
else{
l=mid+1;
}
}
//这样就找到了lx和lr的位置了
if(lx==INT_MAX||rx==-1)
{
return 0;
}
else
{
return rx-lx+1;
}
}
};
/**
* Your RangeFreqQuery object will be instantiated and called as such:
* RangeFreqQuery* obj = new RangeFreqQuery(arr);
* int param_1 = obj->query(left,right,value);
*/实际应该用哈希+二分,我们在询问之前,就用哈希表统计出每一个值在数组中可能出现的位置,然后我们用一个二分来看可能存在的位置是否在询问的区间内,分别找到出现在区间内的最小位置和最大位置,二者之差即为出现的频率次数。
完整的代码如下:
cpp
class RangeFreqQuery {
public:
vector<int> a;
unordered_map<int,vector<int> > mp;
RangeFreqQuery(vector<int>& arr) {
for(int i=0;i<arr.size();i++)
{
a.push_back(arr[i]);
mp[arr[i]].push_back(i);
}
}
int query(int left, int right, int value) {
//排序
vector<int>& temp=mp[value];
if(mp[value].size()==0)
{
return 0;
}
int l=0;
int r=temp.size()-1;
//找第一个大于等于value的位置
//找第一个小于等于value的位置
//如果数组中有value 那么
// 那么这两个位置都一定在value上
int lx=INT_MAX;
while(l<=r)
{
int mid=(l+r)/2;
if(temp[mid]>=left&&temp[mid]<=right)
{
r=mid-1;
lx=min(lx,mid);
}
else if(temp[mid]>right)
{
r=mid-1;
}
else{
l=mid+1;
}
}
//找到最左端的lx value
int rx=-1;
l=0;
r=temp.size()-1;
while(l<=r)
{
int mid=(l+r)/2;
if(temp[mid]>=left&&temp[mid]<=right)
{
l=mid+1;
rx=max(rx,mid);
}
else if(temp[mid]>right){
r=mid-1;
}
else{
l=mid+1;
}
}
//这样就找到了lx和lr的位置了
if(lx==INT_MAX||rx==-1)
{
return 0;
}
else
{
return rx-lx+1;
}
}
};
/**
* Your RangeFreqQuery object will be instantiated and called as such:
* RangeFreqQuery* obj = new RangeFreqQuery(arr);
* int param_1 = obj->query(left,right,value);
*/需要注意的是,在获取哈希表中的某一个值对应的出现位置的数组时,我们要用引用来获取,否则会超时
cpp
vector<int>& temp=mp[value];最终的时间复杂度是O(nlogn)