此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下:
- 原课程视频链接:[双语字幕]吴恩达深度学习deeplearning.ai
- github课程资料,含课件与笔记:吴恩达深度学习教学资料
- 课程配套练习(中英)与答案:吴恩达深度学习课后习题与答案
经过第二周的基础补充,本周内容的理解难度可以说有了很大的降低,主要是从逻辑回归扩展到浅层神经网络,讲解相关内容,我们按部就班梳理课程内容即可,当然,依旧会尽可能地创造一个较为丝滑的理解过程。
我们继续上一篇的内容,来展开一下激活函数 对浅层神经网络拟合效果的影响,并完成浅层神经网络的反向传播部分,这样,我们就大致了解了浅层神经网络相比逻辑回归,是如何提高算法性能的。
1. 浅层神经网络里的激活函数
1.1 隐藏层激活函数的作用
在逻辑回归中,我们知道,最后使用sigmoid激活函数是为了让加权和映射为概率从而实现分类效果。
而现在,如果我们仍要进行二分类,而浅层神经网络输出层的sigmoid函数已经实现了分类效果,那隐藏层再使用激活函数的作用是什么?
我们看一看如果不设隐藏层神经元的激活函数,正向传播的输出是什么形式:
- 首先,隐藏层只有线性组合,那么隐藏层的输出就是加权和本身:
\[\mathbf{Z^{[1]}} = \mathbf{W^{[1]}} \mathbf{X} + \mathbf{b^{[1]}} \]
- 现在,隐藏层的加权和就是输出层的输入,即:
\[\mathbf{Z^{[2]}} = \mathbf{W^{[2]}}( \mathbf{W^{[1]}} \mathbf{X} + \mathbf{b^{[1]}} ) + \mathbf{b^{[2]}} = \mathbf{W^{[2]}}\mathbf{W^{[1]}} \mathbf{X}+(\mathbf{W^{[2]}}\mathbf{b^{[1]}} + \mathbf{b^{[2]}}) \quad (1 \times m) \]
- 我们观察一下就会发现,\(\mathbf{Z^{[2]}}\) 的实际形式没有发生任何变化,我们换一个示例看一下:
\[y = 3(2x+1)+1 =6x+4 \]
可以发现,其形式依旧是"权重 × 输入 + 偏置"的线性表达式。
也就是说,无论我们堆叠多少层这样的"线性层",最后得到的结果仍然等价于一个没有任何非线性能力的线性模型 。这与逻辑回归本质上并没有区别。
在这种情况下,多层和一层的区别就相当于:
\[10 = 1*2*5(多层) \]
\[10 = 1*10(一层) \]
这便是激活函数的核心作用:引入非线性
1.2 激活函数如何引入非线性?
我们已经知道, 在没有激活函数的情况下,神经元的输出是:
\[\mathbf{A^{[1]}} = \mathbf{Z^{[1]}} = \mathbf{W^{[1]}}\mathbf{X} + \mathbf{b^{[1]}} \]
而当我们加入激活函数 \(g(x)\) 后,输出就变成:
\[\mathbf{A^{[1]}} = g(\mathbf{Z^{[1]}}) = g(\mathbf{W^{[1]}}\mathbf{X} + \mathbf{b^{[1]}}) \]
因为此时,下一层的输入就变成了一个经过非线性映射的结果:
\[\mathbf{Z^{[2]}} = \mathbf{W^{[2]}},g(\mathbf{W^{[1]}}\mathbf{X} + \mathbf{b^{[1]}}) + \mathbf{b^{[2]}} \]
这意味着:
如果 \(g(x)\) 是线性的(例如恒等函数 \(g(z)=z\)),网络整体依旧是线性关系;
而只要 \(g(x)\) 是非线性函数 (如 Sigmoid、ReLU、tanh 等),网络整体的映射关系就无法再化简为一个单一的线性变换 。
我们继续刚刚那个例子:
\[y = 3(2x+1)+1 =6x+4 \]
现在我们只改一点,把激活函数换成ReLU,即:
\[g(z) = \max(0, z) \]
隐藏层的传播过程即为:
\[Z^{[1]} = 2x + 1,\quad A^{[1]} = \max(0, 2x+1) \]
再输入输出层:
\[Z^{[2]} = 3A^{[1]} + 1 = 3\max(0, 2x+1) + 1 \]
这个时候,整体的输出函数变成:
\[y = \begin{cases} 6x + 4, & x > -0.5 \\ 1, & x \le -0.5 \end{cases} \]
这就是一个分段线性函数 ,可以拐弯、有"折点",不再是单一直线。
那如果再换成更复杂的激活函数呢?
这也意味着网络具备了拟合非线性关系的能力。
最后看一张图:
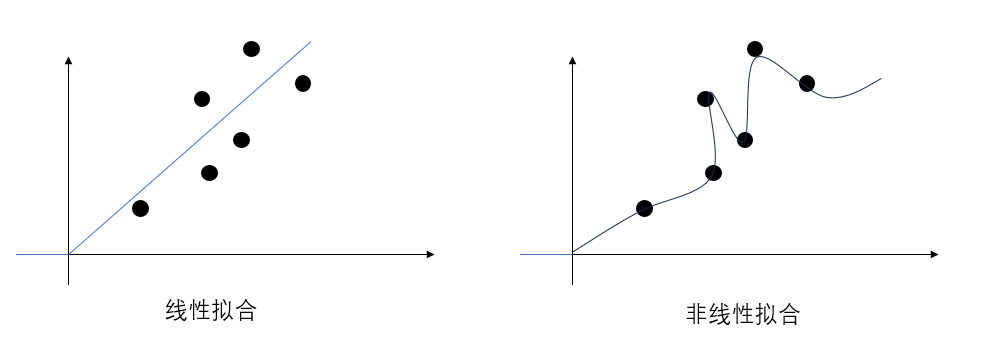
我们想通过图中的几个数据点进行拟合,没有激活函数,我们就只能像左侧一样画一条直线,而只有使用了激活函数,我们才能让这条直线弯曲,来实现更好拟合效果。
1.3 常见的激活函数
在了解了激活函数的作用------为神经网络引入非线性能力之后,我们来看看几种常见的激活函数及其特性。不同的激活函数,会对神经元的输出特征、梯度传播和训练效果产生显著影响。
(1)Sigmoid 函数
Sigmoid 的表达式为:
\[g(z) = \frac{1}{1 + e^{-z}} \]
其输出范围在 \((0, 1)\) 之间,形状如"S"型曲线。
Sigmoid 的优点在于它可以将任意实数映射为 \((0,1)\),非常适合二分类任务的输出层,例如预测概率。
缺点是当输入较大或较小时,梯度接近 0,容易出现梯度消失 问题,导致网络难以训练。

(2)Tanh函数
Tanh 是 Sigmoid 的改进版本,其表达式为:
\[g(z) = \tanh(z) = \frac{e^{z} - e^{-z}}{e^{z} + e^{-z}} \]
输出范围在 \((-1, 1)\) 之间,同样是"S"型曲线。
Tanh 的优点在于输出均值为 0,有助于加快梯度下降的收敛,并在一定程度上缓解了梯度消失问题。
缺点在于,当输入过大或过小时,依然会出现梯度趋于 0 的饱和现象。
如果把 Sigmoid 看作"挤压到 [0,1]",那么 Tanh 就是"挤压到 [-1,1]",更加对称,有利于后续层学习,因此,Tanh比sigmoid更适合作为隐藏层的激活函数。

(3)ReLU函数
ReLU 是目前最常用的激活函数之一,定义为:
\[g(z) = \max(0, z) \]
当输入为正时,输出等于自身;当输入为负时,输出为 0。
ReLU 的优点在于计算简单,梯度传播效率高,并且在正区间保持线性,减少了梯度消失问题,从而加快训练速度。
缺点在于对于负输入,梯度恒为 0,容易出现"神经元死亡"现象,即某些神经元永远输出 0,无法更新。

(4)Leaky ReLU(带泄漏的 ReLU)
为了缓解 ReLU 的"神经元死亡"问题,便出现了 Leaky ReLU:
\[g(z) = \begin{cases} z, & \text{if } z > 0, \\ \alpha z, & \text{if } z \leq 0. \end{cases} \]
其中 \(\alpha\) 是一个很小的常数(通常取 0.01)。Leaky ReLU 的优点在于对负区间保留一个微小的斜率,避免梯度完全为 0,从而训练更加稳定,减少"死神经元"的出现。
缺点是其输出仍然不是严格的零中心,且 \(\alpha\) 的选取需要进行调试。

2.浅层神经网络的反向传播
我们知道,在浅层神经网络里,我们涉及到两个层级各自的权重和偏置,因此,不同于逻辑回归中的一次更新,我们这次需要在一次反向传播过程中,更新两个层级的参数 。
参数的传递过程如下:
\[\begin{aligned} &\text{隐藏层参数(4个神经元):} \\ &\Delta W^{[1]}, \Delta b^{[1]} \;\; \to \;\; \Delta Z^{[1]} \;\; \to \;\; \Delta A^{[1]} \\ \\ &\text{输出层参数(1个神经元):} \\ &\Delta W^{[2]}, \Delta b^{[2]} \;\; \to \;\; \Delta Z^{[2]} \;\; \to \;\; \Delta A^{[2]} \to \;\; \Delta L\\ \end{aligned} \]
2.1 损失函数
我们知道二分类交叉熵成本函数格式如下:
\[\mathcal{L} = -\frac{1}{m} \sum_{i=1}^{m} \Big[ y^{(i)} \log a^{[2](i)} + (1 - y^{(i)}) \log (1 - a^{[2](i)}) \Big] \]
向量化后即可表示为: $$ \mathcal{L}(\mathbf{A^{[2]}}, \mathbf{Y}) $$
我们依旧通过损失函数,使用链式法则来计算梯度。
2.2 输出层梯度
输出层激活函数为 \(sigmoid(x)\)
而输出层误差定义为:
\[\mathbf{dZ^{[2]}} = \frac{\partial \mathcal{L}}{\partial \mathbf{Z^{[2]}}} \]
在第二周的推导中,我们已经知道,对于二分类交叉熵 + sigmoid,损失对加权和的导数可简化为:
\[\mathbf{dZ^{[2]}} = \mathbf{A^{[2]}} - \mathbf{Y} \quad (1 \times m) \]
继续通过链式法则,我们得到输出层权重和偏置的梯度(详细过程可看第二周的推导):
\[\mathbf{dW^{[2]}} = \frac{1}{m} \mathbf{dZ^{[2]}} (\mathbf{A^{[1]}})^T \quad (1 \times 4) \]
\[\mathbf{db^{[2]}} = \frac{1}{m} \sum_{i=1}^{m} \mathbf{dZ^{[2](i)}} \quad (1 \times 1) \]
3.3 隐藏层梯度
对于隐藏层,这里我们便不定义具体的激活函数,用通式来展示过程:
先梳理一下我们现在有的量:
- 损失对输出层加权和的导数\(\mathbf{dZ^{[2]}}\)
- 隐藏层的加权和\(\mathbf{Z^{[1]}}\)
- 隐藏层的的加权和经过激活函数的输出\(\mathbf{A^{[1]}}\)
- 隐藏层的激活函数\(g(\mathbf{Z^{[1]}})\) 和它的导数\(g'(\mathbf{Z^{[1]}})\)
- 隐藏层的参数\(\mathbf{W^{[1]}}\),\(\mathbf{b^{[1]}}\)
现在,我们要求隐藏层参数的梯度,首先要得到损失关于隐藏层输出的导数,即:
\[\mathbf{dA^{[1]}} = \frac{\partial \mathcal{L}}{\partial \mathbf{A^{[1]}}} \]
再通过链式法则细化一下,我们得到:
\[\mathbf{dA^{[1]}} = \mathbf{dZ^{[2]}}⋅ \frac{\partial \mathbf{Z^{[2]}}}{\partial \mathbf{A^{[1]}}} \]
再看一眼加权和公式:
\[\mathbf{Z^{[2]}} = \mathbf{W^{[2]}}\mathbf{A^{[1]}}+ \mathbf{b^{[2]}} \quad (1 \times m) \]
所以,通过求导我们得到:
\[\mathbf{dA^{[1]}} = \mathbf{(W^{[2]})^T}\mathbf{dZ^{[2]}},转置为了匹配维度 \quad (4 \times m)\]
下一步,得到损失关于隐藏层加权和的输出,即:
\[\mathbf{dZ^{[1]}} = \mathbf{dA^{[1]}}⋅ \frac{\partial \mathbf{A^{[1]}}}{\partial \mathbf{Z^{[1]}}} \]
而隐藏层输出对加权和求导,其实就是激活函数的导数:\(g'(\mathbf{Z^{[1]}})\)
因此,我们得到:
\[\mathbf{dZ^{[1]}} = \mathbf{dA^{[1]}}⋅ g'(\mathbf{Z^{[1]}}) \quad (4 \times m) \]
注意!这里的乘是Hadamard 乘。
Hadamard 乘激活导数 = 对每个神经元每个样本的误差单独乘上对应的激活导数
到了这一步,我们就可以得到最后的梯度:
\[\mathbf{dW^{[1]}} = \frac{1}{m} \mathbf{dZ^{[1]}} \mathbf X^T \quad (4 \times n) \]
\[\mathbf{db^{[1]}} = \frac{1}{m} \sum_{i=1}^{m} \mathbf{dZ^{[1]}_{:,i}} \quad (4 \times 1) \]
还没完 ,这里还有一点要强调,注意看这个符号:\(\mathbf{dZ^{[1]}_{:,i}}\)
我们之前的逻辑回归,以及本次传播的输出层偏置,使用的符号都是\(\mathbf{dZ^{(i)}}\),对这个符号求平均就代表对 \(m\) 个样本在同一神经元上的误差求平均 。
而现在,我们的隐藏层有四个神经元,由此解释一下\(\frac{1}{m} \sum_{i=1}^{m} \mathbf{dZ^{[1]}_{:,i}}\) 的含义:
- "\(:\)"代表所有行
- "\(:,i\)"代表第 \(i\) 列
- "\(\sum_{i=1}^{m} \mathbf{dZ^{[1]}_{:,i}}\)"代表对\(dZ^{[1]}\) 的每一列求和,得到的结果是所有样本分别在四个隐藏神经元总误差
- 最后求平均值,即为平均误差,现在, 每个元素就对应一个隐藏神经元的偏置梯度。
我们也总结一下反向传播过程中各个量和其维度:
| 量 | 维度 | 说明 |
|---|---|---|
| X | n × m | 输入特征 |
| W[1] | 4 × n | 隐藏层权重 |
| b[1] | 4 × 1 → 4×m | 隐藏层偏置(广播) |
| Z[1] | 4 × m | 隐藏层线性组合 |
| A[1] | 4 × m | 隐藏层激活输出 |
| W[2] | 1 × 4 | 输出层权重 |
| b[2] | 1 × 1 → 1×m | 输出层偏置(广播) |
| Z[2] | 1 × m | 输出层线性组合 |
| A[2] | 1 × m | 输出层激活输出 |
| dZ[2] | 1 × m | 输出层误差 |
| dW[2] | 1 × 4 | 输出层权重梯度 |
| db[2] | 1 × 1 | 输出层偏置梯度 |
| dA[1] | 4 × m | 输出层误差传回隐藏层 |
| dZ[1] | 4 × m | 隐藏层误差(Hadamard乘激活导数) |
| dW[1] | 4 × n | 隐藏层权重梯度 |
| db[1] | 4 × 1 | 隐藏层偏置梯度 |
3.4 更新参数
在完成所有梯度计算后,我们就可以使用梯度下降法来更新网络的权重和偏置,公式如下:
(1) 输出层参数更新
\[\mathbf{W^{[2]}} := \mathbf{W^{[2]}} - \eta \mathbf{dW^{[2]}} \]
\[\mathbf{b^{[2]}} := \mathbf{b^{[2]}} - \eta \mathbf{db^{[2]}} \]
(2) 隐藏层参数更新
\[\mathbf{W^{[1]}} := \mathbf{W^{[1]}} - \eta \mathbf{dW^{[1]}} \]
\[\mathbf{b^{[1]}} := \mathbf{b^{[1]}} - \eta \mathbf{db^{[1]}} \]
这样,我们就完成了浅层神经网络的一个反向传播过程的梳理。
相比逻辑回归,浅层神经网络在一次反向传播中更新了两层参数,而在之后的更复杂的神经网络结构中,隐藏层数量也不只一层,这样,在一次反向传播中,就会更新更多的参数。
但其形式,也只是像现在这样的通过链式法则的层层求导,更新即可。
所以,之后便会尽量少的出现这样比较繁杂的求导,但前提是要了解神经网络通过反向传播更新参数的逻辑。
下一篇即为本周理论部分的最后一部分,是神经网络的参数初始化,也是多个隐藏层神经元能发挥不同作用的原因。