C语言数据结构：算法复杂度（2）

1.常数阶 O(1)
定义：算法所需额外空间不随问题规模 n 变化，为固定常量。
实例：
cpp 复制代码
void swap(int a, int b) {  // 局部变量a、b为固定空间，与n无关
    int temp = a;
    a = b;
    b = temp;
}
解释：无论输入的 a、b 多大，仅使用3个局部变量（a、b、temp），空间复杂度为 O(1)。
2. 线性阶 O(n)
定义：额外空间随问题规模 n 线性增长。
实例：
cpp 复制代码
void create(int n)
{
    int arr[n];  // 动态数组，空间大小随n变化
}
解释：一维数组 arr[n] 占用 n 个整数空间，空间复杂度为 O(n)。

3. 二维阶 O(n×m)
定义：额外空间随两个问题规模 n 和 m 的乘积增长，常见于二维数组。
实例：
cpp 复制代码
void create(int n, int m)
{
    int a[n][m];  // 二维数组，空间大小为n×m
}
解释：二维数组 matrix[n][m] 占用 n×m 个整数空间，空间复杂度为 O(n×m)。

4. 递归阶 O(n)（递归调用栈）
定义：递归算法中，每次调用会在栈上分配空间，递归深度决定空间复杂度。
实例：
cpp 复制代码
int factorial(int n)    // 递归计算n的阶乘
{
    if (n == 0) return 1;
    return n * factorial(n - 1);
}
解释：递归调用深度为 n（从 n 到 0），每次调用占用固定栈空间，总空间复杂度为 O(n)。

举例一下上篇文章的题：

C语言数据结构：算法复杂度（1）

时间复杂度偏复杂的上下界的案例：冒泡排序代码题：

原代码：

cpp 复制代码

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include<stdlib.h>
#include<time.h>
void test(int *a, int n)
{
    int i, j;
    for (i = 0; i < n - 1; i++)    // 外层循环：n-1轮（每轮确定一个最小元素的位置）
    {
        int exchange = 0;         // 优化标志：判断本轮是否发生交换
        // 内层循环：从左向右遍历，将最小元素"冒泡"到数组前端（i位置）
        for (j = 1; j < n - i; j++)    // 终止条件：j < n - i（已排序部分无需再比较）
        {
            if (a[j] > a[j - 1])       // 降序排序：前一个元素 < 后一个元素时交换
            {
                int t = a[j];
                a[j] = a[j - 1];
                a[j - 1] = t;
                exchange = 1;         // 标记发生交换
            }
        }
        if (exchange == 0)    // 若本轮无交换，数组已有序，提前退出
        {
            break;
        }
    }
}
int main()
{
    srand(time(0));
    int m,n;
    printf("请输入数组中值的个数\n");
    scanf("%d",&n);
    int i;
    int * a=(int *)malloc(sizeof(int)*n);
    for(i=0; i<n; i++)
    {
        a[i]=rand()%100;
    }
    test(a,n);
}

现在对该代码的空间复杂度进行分析：（要分析代码）

cpp 复制代码

void test(int *a, int n)
{
    int i, j;
    for (i = 0; i < n - 1; i++)    
    {
        int exchange = 0;     
        for (j = 1; j < n - i; j++)   
        {
            if (a[j] > a[j - 1])      
            {
                int t = a[j];
                a[j] = a[j - 1];
                a[j - 1] = t;
                exchange = 1;       
            }
        }
        if (exchange == 0)   
        {
            break;
        }
    }
}

上文曾说过函数运⾏时所需要的栈空间(存储参数、局部变量、⼀些寄存器信息等)在编译期间已经确定好了，因此空间复杂度主要通过函数在运⾏时候显式申请的额外空间来确定。

所以我们要关注函数内申请的空间，函数中仅申请4个局部变量，所以可知空间复杂度为 O(1)。

二、常见复杂度对比

介绍

接下来我会展示那些核心的复杂度类型及特征 以及各个函数随的增长函数值的变化情况。

以下是编程中最常见的复杂度类型，按效率从高到低排序：

复杂度符号	名称	数学表达	增长趋势	典型场景/算法
O(1)	常数时间复杂度	不随n变化	执行时间固定，与输入规模无关	数组索引访问、哈希表查找、简单算术运算（如判断奇偶）
O(log n)	对数时间复杂度	log₂n 或 logₖn	随n缓慢增长，数据规模翻倍时仅增加1次操作	二分查找、平衡二叉树（AVL树/红黑树）的插入/查询、快速幂运算
O(n)	线性时间复杂度	n	执行时间与n成正比	数组遍历、单链表遍历、求和/求最大值（需完整扫描数据）
O(n log n)	线性对数时间复杂度	n·log₂n	比线性增长稍快，但远低于平方级	高效排序算法（归并排序、快速排序、堆排序）、分治策略解决的问题（如最近点对）
O(n²)	平方时间复杂度	n²	执行时间随n平方增长	嵌套循环（如冒泡排序、插入排序）、邻接矩阵遍历、简单动态规划（如斐波那契递归）
O(n³)	立方时间复杂度	n³	执行时间随n立方增长	三重嵌套循环（如矩阵乘法、弗洛伊德最短路径算法）
O(2ⁿ)	指数时间复杂度	2ⁿ	随n指数级爆炸增长	递归子集枚举、未优化的斐波那契数列（递归实现）、汉诺塔问题
O(n!)	阶乘时间复杂度	n!	增长速度远超指数级，几乎不可用	全排列生成（如旅行商问题的暴力解法）

关键对比与应用建议

效率边界：
- 高效算法（O(1)~O(n log n)）：适用于大规模数据（如n=10⁶），例如数据库索引查询（O(log n)）、大数据排序（O(n log n)）。
- 低效算法（O(n²)及以上）：仅适用于小规模数据（如n<10³），例如小规模数组的简单排序（冒泡排序）、特定场景的动态规划（如n=100的状态转移）。

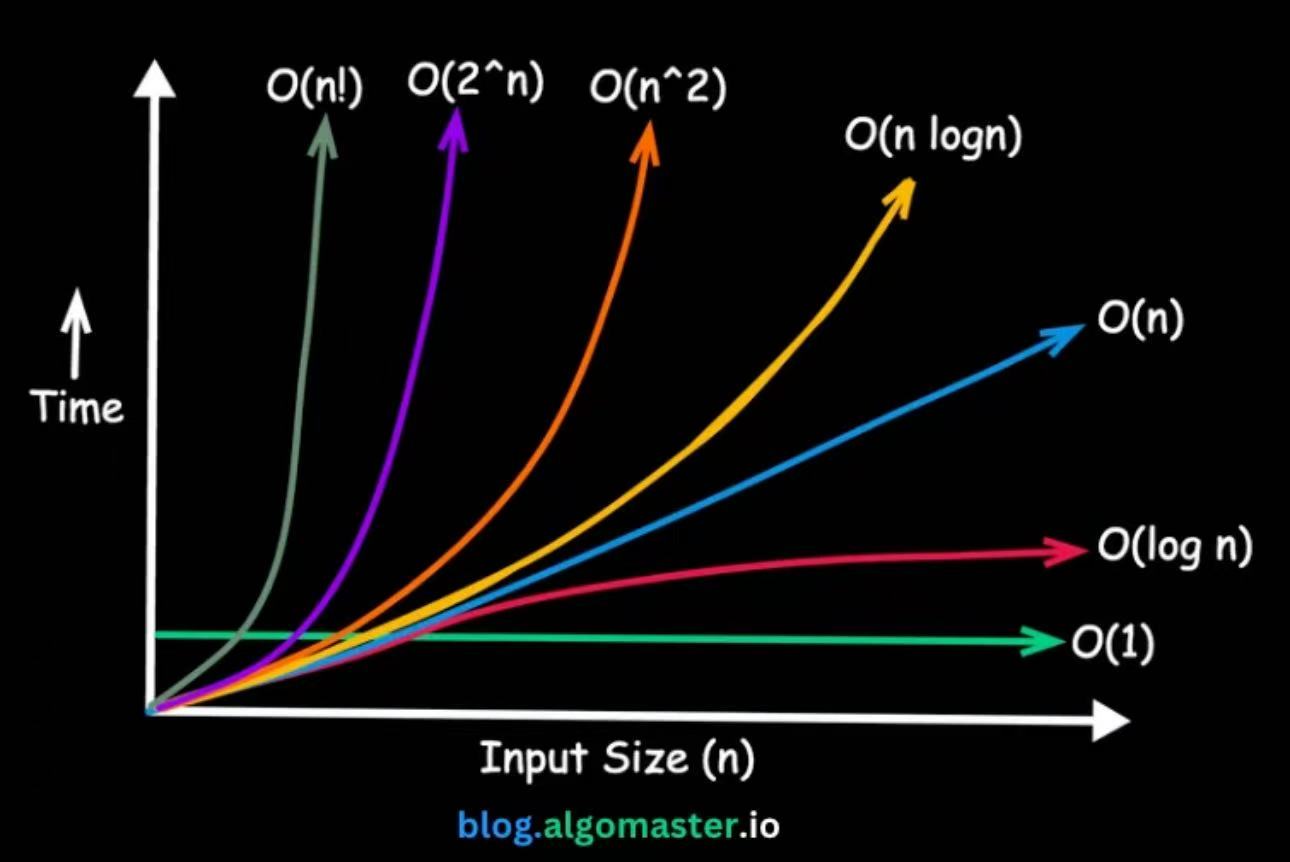
各个函数随的增长函数值的变化情况：

图示：

三、常见复杂度算法题

介绍常见复杂度算法题以及讲解

现在来解决一下上篇文章的题：

C语言数据结构：算法复杂度（1）

举个例题： https://leetcode.cn/problems/rotate-array/description/

189. 轮转数组 - 力扣（LeetCode）结合前文讲解的知识，我们可通过算法优化来解决问题：

先看题：

在1中的写法上一篇文章讲解过了，并且提交方面失败了，所以就不再讲那种写法：

接下来讲些复杂度小的解法：

解1：

我们可以通过创建一个新数组，用于存储轮转后的结果，原数组也不就用来回的移动多次了，最后在将新数组的值遍历复制到原数组中。

：

cpp 复制代码

void rotate(int* nums, int numsSize, int k) {
   if(k>numsSize)
   {
     k%=numsSize;
   }
  int *tmp=(int *)malloc(sizeof(int)*numsSize);
  int i;
  for(i=0;i<numsSize;i++)
  {
    tmp[(i+k)%numsSize]=nums[i];
  }
  for(i=0;i<numsSize;i++)
  {
    nums[i]=tmp[i];
  }
}

由上可知，该解法通过：（时间复杂度：O(N)，空间复杂度：O(N)）

旋转实现方式 ：通过创建临时数组 tmp，将原数组元素按旋转后的位置存入 tmp，再复制回原数组。

核心公式：tmp[(i + k) % numsSize] = nums[i]（通过取模确保索引不越界）。

k 值处理 ：当 k > numsSize 时，通过 k %= numsSize 优化旋转次数（例如，旋转 5 次等效于旋转 0 次）。

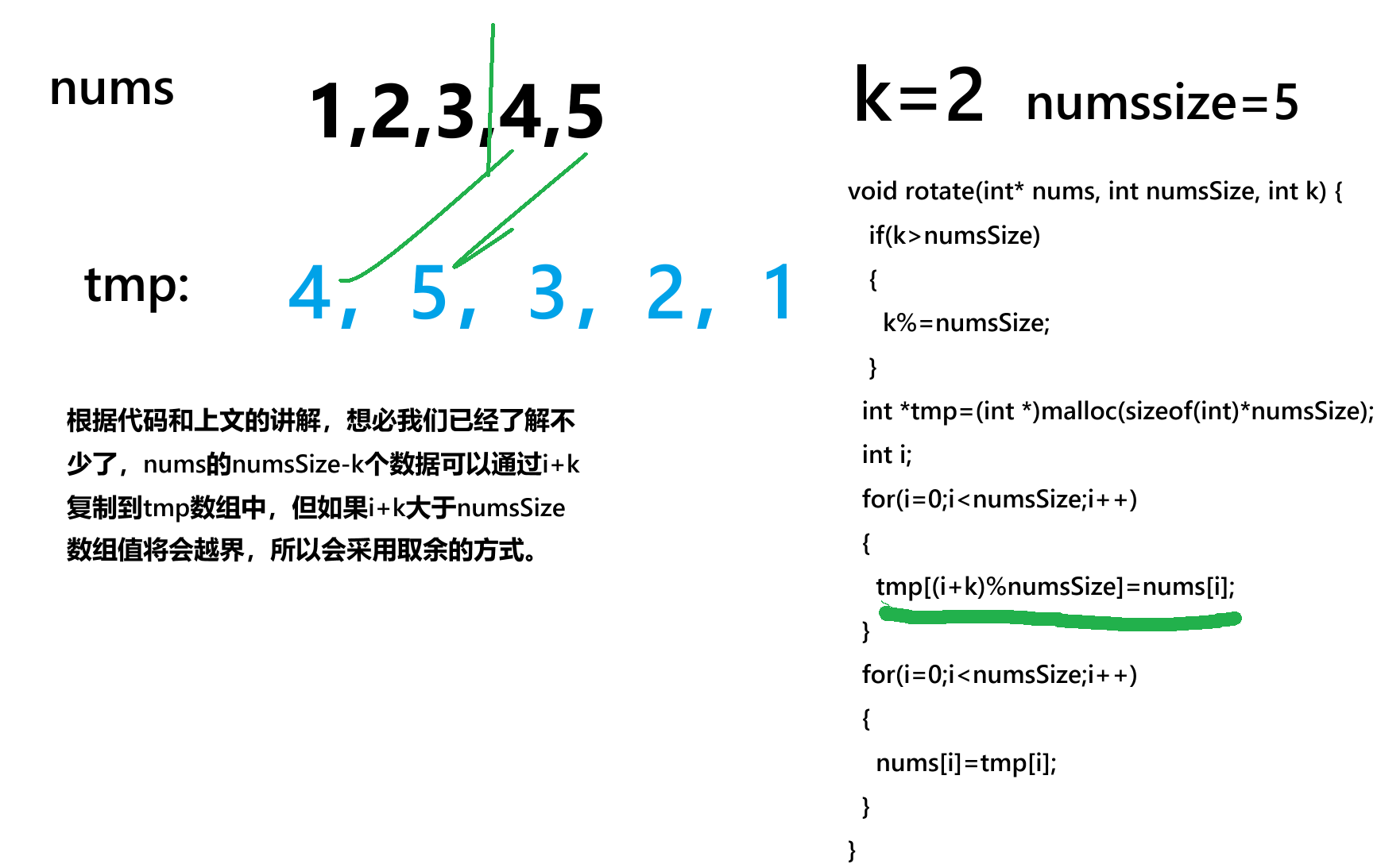
该解法虽然时间复杂度降下来了，但是空间复杂度上去了，这种思想就是所谓"空间换时间"（时间复杂度：O(N)，空间复杂度：O(N)）。

解2：

对数组逆置：大致思路：分3次逆置，1. 将numssize-k个值逆置，2. 将后k个值逆置，3. 将全部值逆置。

三次逆置法 是一种 空间复杂度O(1) 的高效旋转算法，核心思想是通过局部逆置和整体逆置的组合，实现数组旋转效果。

：

cpp 复制代码

void ni(int *nums,int left,int right)
{   while(left<right)
{
    int tmp=nums[left];
    nums[left]=nums[right];
 nums[right]=tmp;
 left++;
 right--;
}

}
void rotate(int* nums, int numsSize, int k) {
   if(k>numsSize)
   {
     k%=numsSize;
   }
  ni(nums,0,numsSize-k-1);
  ni(nums,numsSize-k,numsSize-1);
  ni(nums,0,numsSize-1);
}

解释：

该解法时间复杂度：O(N)，空间复杂度：O(1)。

核心思想：通过三次局部反转实现整体旋转，避免使用额外数组（空间优化）。

左旋/右旋转换 ：若需实现左旋 k 步 ，可将 k 转换为 numsSize - k 后调用该函数（如左旋 2 步 = 右旋 3 步，当 numsSize=5 时）。

总结

以上就是今天要讲的内容，本篇文章涉及的知识点为：空间复杂度、常见复杂度对比等知识的相关内容，为本章节知识的内容，希望大家能喜欢我的文章，谢谢各位，接下来的内容我会很快更新，下篇文章为讲解顺序表，顺序结构相关知识。