利用舵机实现机器人行走

jerryinwuhan2025-10-19 12:02

文章目录

    • [**完整可运行的 Python 示例**，](#完整可运行的 Python 示例，)
  • 一、运动学（简洁明确）
    • [1. 机械模型（简化）](#1. 机械模型（简化）)
    • [2. 正运动学（给角度求足端位置）](#2. 正运动学（给角度求足端位置）)
    • [3. 逆运动学（给目标前后位移求角度）](#3. 逆运动学（给目标前后位移求角度）)
    • [4. 从"足端轨迹"到"推进力"](#4. 从“足端轨迹”到“推进力”)
  • 二、步态（Gait）设计
  • [三、代码（完整 --- 使用 gpiozero.AngularServo）](#三、代码（完整 — 使用 gpiozero.AngularServo）)
  • 四、代码要点说明与调参建议
  • 五、进阶改进建议（如果你想进一步开发）
    • [🧩 一、8舵机四足机器人结构](#🧩 一、8舵机四足机器人结构)
    • [🦿 二、简化运动学模型](#🦿 二、简化运动学模型)
      • [1️⃣ 正运动学（Forward Kinematics）](#1️⃣ 正运动学（Forward Kinematics）)
      • [2️⃣ 逆运动学（Inverse Kinematics）](#2️⃣ 逆运动学（Inverse Kinematics）)
    • [🧠 三、步态设计（对角步 Trot Gait）](#🧠 三、步态设计（对角步 Trot Gait）)
    • [⚙️ 四、完整 Python 示例（8个舵机 + 运动学）](#⚙️ 四、完整 Python 示例（8个舵机 + 运动学）)
    • [🧾 五、代码讲解（运动学 & 步态）](#🧾 五、代码讲解（运动学 & 步态）)
    • [🧮 六、简单数值例子（逆运动学验证）](#🧮 六、简单数值例子（逆运动学验证）)
    • [⚡ 七、调试与建议](#⚡ 七、调试与建议)
    • [🧭 八、总结（与4舵机版对比）](#🧭 八、总结（与4舵机版对比）)
    • [**CPG（中央模式发生器）控制框架**，用于那台 **8 舵机 / 2 DOF 每腿** 的四足机器人。](#CPG（中央模式发生器）控制框架，用于那台 8 舵机 / 2 DOF 每腿 的四足机器人。)
  • 1) CPG 简介与数学（直接可用） CPG 简介与数学（直接可用）)
  • 2) 完整 Python 代码（含模拟和硬件两种模式） 完整 Python 代码（含模拟和硬件两种模式）)
  • 3) 如何通过 CPG 参数调节不同步态与运动特性 如何通过 CPG 参数调节不同步态与运动特性)
  • 4) 调试步骤（推荐顺序） 调试步骤（推荐顺序）)
    • [**8舵机步行机器人基础运动学系统**，接下来加上"**原地转向 / 后退 / 侧移**"是非常自然的一步。](#8舵机步行机器人基础运动学系统，接下来加上“原地转向 / 后退 / 侧移”是非常自然的一步。)
    • [🧠 一、运动学思想：通过足端轨迹叠加生成机体运动](#🧠 一、运动学思想：通过足端轨迹叠加生成机体运动)
    • [⚙️ 二、核心步态生成器 (Gait Generator)](#⚙️ 二、核心步态生成器 (Gait Generator))
    • [🧩 三、不同动作的相位/方向配置](#🧩 三、不同动作的相位/方向配置)
    • [🧮 四、完整 Python 控制框架](#🧮 四、完整 Python 控制框架)
    • [📘 五、运动学解释（以原地转向为例）](#📘 五、运动学解释（以原地转向为例）)
    • [🧭 六、动作总结](#🧭 六、动作总结)

完整可运行的 Python 示例，

它用 4 个舵机 （每条腿 1 个舵机）来实现一个非常基础的四足机器人"行走"动作，并且把相关的运动学（正/逆 kinematics）、

重要提醒：只有 1 个舵机/腿（即每条腿只有一个转动自由度）时，机器人只能做非常受限的步态 ------ 主要是前后摆动（在一个平面内推拉地面）而不能做真正的抬腿/降落和复杂足端定位。下面的实现是基于这种受限硬件的"实用折衷" ------ 通过协调前后摆动（trot/two-beat gait）产生向前推进力。

一、运动学（简洁明确）

1. 机械模型（简化）

  • 每条腿由一个舵机在"髋关节"处控制，舵机驱动在**矢状面（前-后）**旋转（类似人在前后摆腿），角度记为 θ \theta θ（以垂直向下/中位为 0° 为参考）。

  • 每条腿等效为刚性连杆，长度为 L L L。足端（脚）相对于髋关节的位置：

    x = L sin ⁡ ( θ ) ( 前为正 ) x = L \sin(\theta) \quad (\text{前为正}) x=Lsin(θ)(前为正)

    z = L cos ⁡ ( θ ) ( 垂直方向，正向向下 ) z = L \cos(\theta) \quad (\text{垂直方向，正向向下}) z=Lcos(θ)(垂直方向，正向向下)

    （注意这里只用到平面 x x x- z z z，横向 y y y 忽略，因为舵机不控制横向）

2. 正运动学（给角度求足端位置）

  • 给定舵机角度 θ \theta θ，脚在机器人机身坐标系（前为正）上的前后坐标就是 x = L sin ⁡ θ x = L \sin\theta x=Lsinθ。
  • 舵机角度越向前，脚端 x x x 越前；角度向后，脚端 x x x 越后。

3. 逆运动学（给目标前后位移求角度）

  • 如果你把目标足端前后坐标设为 x d x_{d} xd（且 ∣ x d ∣ ≤ L |x_d| \le L ∣xd∣≤L），对应角度

    θ = arcsin ⁡ ( x d L ) \theta = \arcsin\left(\frac{x_d}{L}\right) θ=arcsin(Lxd)

  • 逆解需要保证 ∣ x d ∣ ≤ L |x_d| \le L ∣xd∣≤L；并且舵机的物理转角范围也受限（比如 [ − 4 5 ∘ , + 4 5 ∘ ] [-45^\circ, +45^\circ] [−45∘,+45∘]），因此可走的步幅受限。

4. 从"足端轨迹"到"推进力"

  • 在真实机器人中，推进力来自"支撑腿"与地面之间的摩擦产生的推力。我们用一种近似方法：

    • 当脚放到后方 并将舵机转向前推（从后摆到前摆）时，与地面的摩擦产生向前推动力 -> 机器人向前移动；
    • 当脚处于前方回收时，尽量减少与地面的接触力（真实机器人会抬脚）；但我们此处只能将脚快速移到前方并尽量减少推力（通过快速回摆或把角度收回到中位），从而实现"步进"效果。

二、步态（Gait）设计

  • 使用经典的 对角步（trot）：同时移动左前(LF) + 右后(RH) 为一组，右前(RF) + 左后(LH) 为另一组。交替进行。

  • 每一步分两相：

    1. 支撑相（push）：支撑腿从后摆到前摆以产生推力（慢速、有力）
    2. 回收相（return）：另一对腿快速从前摆回到后方，为下一次支撑做准备（快速、轻触）

  • 由于没有抬腿，我们用"快速回摆"来尽量减小回收相时对地面的推力。

三、代码（完整 --- 使用 gpiozero.AngularServo）

下面代码实现：

  • Quadruped 类抽象化四条腿（LF, RF, LH, RH）
  • 可配置舵机引脚、连杆长度 L、舵机角度范围与步幅（前后位移）
  • step_forward() 实现单步（两相交替）
  • walk(steps, speed) 实现多步行走
  • 安全释放 GPIO、外接供电提示
python 复制代码 
"""
四足机器人（4 个舵机）行走示例
硬件假设：
 - 每条腿一个舵机（髋关节），控制前后摆动（矢状面）
 - 舵机最好是 AngularServo（以角度控制），若没有可用普通 Servo，但需要自己 map
 - 请确保舵机电源能提供足够电流（外接 5V 电源并共地）

连接示例（BCM 编号）：
 LF (左前)  -> GPIO 17
 RF (右前)  -> GPIO 27
 LH (左后)  -> GPIO 22
 RH (右后)  -> GPIO 23
"""

from gpiozero import AngularServo
from time import sleep
import math

# ========== 参数（按需修改） ==========
# 舵机引脚映射（BCM）
PINS = {
    "LF": 17,
    "RF": 27,
    "LH": 22,
    "RH": 23,
}

# 每条腿连杆长度（米）------ 只是用于运动学计算展示，实际角度由舵机控制决定
L = 0.08  # 8 cm，按你的机械臂长度调整

# 舵机角度范围（物理限制） --- 以中位 0 度为参考
MIN_ANGLE = -45  # 向后最大
MAX_ANGLE = 45   # 向前最大

# 步幅参数（足端前后位移, 单位：米）- 必须满足 |x| <= L
STEP_FORWARD = 0.03  # 支撑相推力时，足端前方位置（m）
STEP_BACK = -0.03    # 回收准备时，足端后方位置（m）

# 时间参数（秒）
PUSH_TIME = 0.35     # 支撑相（慢，产生推力）
RETURN_TIME = 0.15   # 回收相（快，尽量减少与地面接触时间）
PAUSE_BETWEEN_STEPS = 0.05

# 舵机脉宽（根据实际舵机可调整）
MIN_PULSE = 0.5/1000
MAX_PULSE = 2.5/1000

# =======================================

def x_to_angle_deg(x, L):
    """
    逆运动学：给定足端前后位移 x（相对于髋关节，前为正），计算舵机角度（deg）
    θ = arcsin(x / L)
    注意：如果 |x| > L 则超出可达范围，会被夹到 ±90°，但物理舵机有更小角度限制。
    """
    if abs(x) > L:
        # 限制在可达范围
        x = max(min(x, L), -L)
    theta_rad = math.asin(x / L)  # 返回弧度
    theta_deg = math.degrees(theta_rad)
    return theta_deg

class Quadruped:
    def __init__(self, pins, L=0.08,
                 min_angle=MIN_ANGLE, max_angle=MAX_ANGLE,
                 min_pulse=MIN_PULSE, max_pulse=MAX_PULSE):
        self.L = L
        self.min_angle = min_angle
        self.max_angle = max_angle
        # 创建 AngularServo（角度接口）
        self.servos = {}
        for leg, pin in pins.items():
            # AngularServo(angle_range=(min_angle, max_angle)) 也可用，但 gpiozero 的 AngularServo
            # 的默认 angle_range 是 (-90, 90). 我们在设定 angle 时再进行夹位。
            self.servos[leg] = AngularServo(pin,
                                            min_angle=min_angle,
                                            max_angle=max_angle,
                                            min_pulse_width=min_pulse,
                                            max_pulse_width=max_pulse)
        # 初始都回中位
        self.set_all_angles(0)
        sleep(0.5)

    def set_angle(self, leg, angle_deg):
        """设置指定腿的角度（度），会自动裁剪到 min/max"""
        a = max(min(angle_deg, self.max_angle), self.min_angle)
        self.servos[leg].angle = a

    def set_all_angles(self, angle_deg):
        for leg in self.servos:
            self.set_angle(leg, angle_deg)

    def set_foot_x(self, leg, x):
        """给定足端 x（m），通过逆运动学设置舵机角度"""
        ang = x_to_angle_deg(x, self.L)
        self.set_angle(leg, ang)

    def step_forward(self):
        """
        执行一步（trot 对角步）：
         - 相位 A: 支撑组 (LF, RH) 推（慢从后摆到前）
                   回收组 (RF, LH) 快速回摆到后方准备
         - 相位 B: 支撑组 swap (RF, LH) 推，另两条回收
        """
        # 相位 A
        supporting = ("LF", "RH")
        recovering = ("RF", "LH")
        # 恢复组调到后方预备（快速回收）
        for leg in recovering:
            self.set_foot_x(leg, STEP_BACK)
        # 支撑组移动：从后方向前，分帧平滑插值
        frames = 6
        for i in range(frames + 1):
            t = i / frames
            # 支撑组角度插值：从 STEP_BACK -> STEP_FORWARD
            for leg in supporting:
                x = STEP_BACK + (STEP_FORWARD - STEP_BACK) * t
                self.set_foot_x(leg, x)
            # 恢复组维持 STEP_BACK（或者微调整为中位以减少接触）
            sleep(PUSH_TIME / frames)
        sleep(PAUSE_BETWEEN_STEPS)
        # 切换：相位 B
        supporting = ("RF", "LH")
        recovering = ("LF", "RH")
        for leg in recovering:
            # 对刚完成推力的腿，快速回到后方（回收）
            self.set_foot_x(leg, STEP_BACK)
        frames = 6
        for i in range(frames + 1):
            t = i / frames
            for leg in supporting:
                x = STEP_BACK + (STEP_FORWARD - STEP_BACK) * t
                self.set_foot_x(leg, x)
            sleep(PUSH_TIME / frames)
        # 一步结束
        sleep(PAUSE_BETWEEN_STEPS)

    def walk(self, steps=4, speed=1.0):
        """
        连续行走 steps 步。
        speed 值会影响整体节奏：speed>1 更快，<1 更慢
        """
        # 将时间参数按 speed 缩放
        global PUSH_TIME, RETURN_TIME
        base_push = PUSH_TIME
        base_return = RETURN_TIME
        push = base_push / speed
        ret = base_return / speed

        # 简单实现：循环调用 step_forward
        for i in range(steps):
            print(f"Step {i+1}/{steps}")
            # 直接调用 step_forward()，该函数内部使用 PUSHTIME 全局
            self.step_forward()
        # 结束后置中
        self.set_all_angles(0)

    def turn_in_place(self, direction="left"):
        """
        一个非常简单的原地转（利用左右两侧生成不均衡推力）
        direction: "left" 或 "right"
        """
        if direction == "left":
            # 让左侧腿倾向推动更强（例如更大的 STEP_FORWARD），右侧回收
            self.set_foot_x("LF", STEP_FORWARD)
            self.set_foot_x("LH", STEP_FORWARD)
            self.set_foot_x("RF", STEP_BACK)
            self.set_foot_x("RH", STEP_BACK)
        else:
            self.set_foot_x("RF", STEP_FORWARD)
            self.set_foot_x("RH", STEP_FORWARD)
            self.set_foot_x("LF", STEP_BACK)
            self.set_foot_x("LH", STEP_BACK)
        sleep(0.4)
        # 回到中位
        self.set_all_angles(0)

    def close(self):
        for s in self.servos.values():
            try:
                s.close()
            except Exception:
                pass

# ========== 使用示例 ==========
if __name__ == "__main__":
    robot = Quadruped(PINS, L=L)
    try:
        print("初始化完毕 -> 中位")
        sleep(1)

        print("单步示范：走 4 步")
        # 走 4 步
        for _ in range(4):
            robot.step_forward()
            sleep(0.1)

        print("演示：原地向左转")
        robot.turn_in_place("left")

        print("返回中位并退出")
    except KeyboardInterrupt:
        print("用户中断")
    finally:
        robot.close()
        print("清理完成，GPIO 释放。")

四、代码要点说明与调参建议

  1. 舵机与角度映射

    我使用 AngularServo.angle = deg 来直接设置角度，内部由 gpiozero 负责把角度映射到脉宽。若你的舵机或板子对角度映射不准确，请调整 min_pulse_width / max_pulse_width，或微调 MIN_ANGLE/MAX_ANGLE。

  2. 步幅 STEP_FORWARD / STEP_BACK

    • 这些值是"足端相对于髋关节的前后位置（米）"，必须满足 ∣ x ∣ ≤ L |x| \le L ∣x∣≤L（不可超出连杆长度）。
    • 若步幅太大舵机会饱和（到达角度极限）或产生过大扭矩。开始时建议小于连杆长度的 0.3~0.4 倍测试。

  3. PUSH_TIME / RETURN_TIME

    • 支撑相（推）应更缓慢，产生较大接触时间，从而获得推进力。
    • 回收相尽量快速，减少阻碍前进。
    • 根据舵机速度和机械摩擦调节时间以获得稳定推进。

  4. 牵引与外部电源

    • 舵机瞬态电流大，建议使用外接稳定 5V 电源，且确保与树莓派 GND 共地。
    • 若用树莓派 5V 供电，注意电流限制与 USB 供电能力。

  5. 为什么不能像真正四足那样走得稳？

    • 真正的四足机器人通常每条腿至少 2~3 个自由度（髋+膝或更多），可以实现抬腿、避障与稳定足端着地。
    • 仅 1 DOF/腿无法抬脚，因此回收相仍会与地面接触，行走效率和稳定性受限。这个示例更像"摇摆推进"的简化模型，适合作为硬件受限下的学习原型。

五、进阶改进建议（如果你想进一步开发）

  • 把每条腿扩展到 2 DOF（髋 + 膝）或 3 DOF ，实现真实抬腿/着地轨迹，使用完整的逆运动学（IK）规划空间轨迹（例如 x,y,z -> joint angles）。
  • 用 pid 或 imu 做姿态控制，保持机身平衡。
  • 使用 pigpio 后端提高 PWM 精度与同步性。
  • 实现更高级步态（walk, trot, pace, bound）并通过中心模态控制（Central Pattern Generator, CPG）来产生稳定步态。

8个舵机的四足机器人 ------也就是每条腿2个舵机（2自由度 / 2 DOF per leg）的结构。
这就可以实现真正的「抬腿 + 向前摆动」动作，成为一个具备完整步态运动学的基础四足机器人模型。

🧩 一、8舵机四足机器人结构

每条腿有 2 个舵机：

关节 功能 控制方向 举例角度
髋关节（Hip） 前后摆动（推进） 水平面 (x方向) -45° ~ +45°
膝关节（Knee） 抬腿/放腿（上下） 垂直面 (z方向) 0°（伸直）~ 90°（弯曲）

这样整机就有：

  • 4 个髋关节舵机（LF_hip, RF_hip, LH_hip, RH_hip）
  • 4 个膝关节舵机（LF_knee, RF_knee, LH_knee, RH_knee）

🦿 二、简化运动学模型

我们把每条腿看作一个二连杆机构（2-Link Manipulator）：

复制代码 
       (hip)
        o------(L1)------o------(L2)------o (foot)
        θ1               θ2
  • L1：大腿长度
  • L2：小腿长度
  • θ1：髋关节角度（相对于机身垂直向下为 0°）
  • θ2：膝关节角度（相对于大腿）

1️⃣ 正运动学（Forward Kinematics）

给定角度 θ1, θ2，足端坐标为：

x = L 1 sin ⁡ ( θ 1 ) + L 2 sin ⁡ ( θ 1 + θ 2 ) x = L_1 \sin(\theta_1) + L_2 \sin(\theta_1 + \theta_2) x=L1sin(θ1)+L2sin(θ1+θ2)

z = − L 1 cos ⁡ ( θ 1 ) − L 2 cos ⁡ ( θ 1 + θ 2 ) z = -L_1 \cos(\theta_1) - L_2 \cos(\theta_1 + \theta_2) z=−L1cos(θ1)−L2cos(θ1+θ2)

其中 z 向下为正。

2️⃣ 逆运动学（Inverse Kinematics）

给定目标足端 (x, z)，求 θ1, θ2：

cos ⁡ ( θ 2 ) = x 2 + z 2 − L 1 2 − L 2 2 2 L 1 L 2 \cos(\theta_2) = \frac{x^2 + z^2 - L_1^2 - L_2^2}{2 L_1 L_2} cos(θ2)=2L1L2x2+z2−L12−L22

θ 2 = arccos ⁡ ( 上式 ) \theta_2 = \arccos(\text{上式}) θ2=arccos(上式)

θ 1 = arctan ⁡ 2 ( x , − z ) − arctan ⁡ 2 ( L 2 sin ⁡ ( θ 2 ) , L 1 + L 2 cos ⁡ ( θ 2 ) ) \theta_1 = \arctan2(x, -z) - \arctan2(L_2 \sin(\theta_2), L_1 + L_2 \cos(\theta_2)) θ1=arctan2(x,−z)−arctan2(L2sin(θ2),L1+L2cos(θ2))

🧠 三、步态设计（对角步 Trot Gait）

使用对角步（Trot）：

  • 同时移动左前 + 右后（LF, RH）
  • 同时移动右前 + 左后（RF, LH）

每条腿的足端轨迹：

  • 抬起 → 向前摆动 → 放下 → 向后推地

典型的足端轨迹可以在平面上表示为一个循环椭圆：

x ( t ) = x c + A sin ⁡ ( ω t ) x(t) = x_c + A \sin(\omega t) x(t)=xc+Asin(ωt)

z ( t ) = z c + B cos ⁡ ( ω t ) z(t) = z_c + B \cos(\omega t) z(t)=zc+Bcos(ωt)

其中：

  • A A A：步幅（前后）
  • B B B：抬脚高度
  • z c z_c zc：平衡高度
  • ω = 2 π / T \omega = 2\pi/T ω=2π/T：步频角速度

⚙️ 四、完整 Python 示例（8个舵机 + 运动学）

🚨 注意：运行前请确保外接5V电源供舵机，电流足够。

以下代码假设你用 gpiozero.AngularServo 控制每个舵机。

python 复制代码 
"""
8舵机四足机器人行走示例（2自由度/腿）
By 崔乘玮 & Sebastian
"""

from gpiozero import AngularServo
from time import sleep
import math

# ================== 参数 ==================
# 每条腿两个舵机：hip（髋关节），knee（膝关节）
# BCM 引脚分配：
PINS = {
    "LF_hip": 17,  "LF_knee": 18,
    "RF_hip": 27,  "RF_knee": 22,
    "LH_hip": 23,  "LH_knee": 24,
    "RH_hip": 25,  "RH_knee": 5,
}

# 连杆长度 (m)
L1 = 0.05  # 大腿
L2 = 0.05  # 小腿

# 舵机角度范围
MIN_ANGLE = -90
MAX_ANGLE = 90

# 脉宽范围（根据舵机调整）
MIN_PULSE = 0.5/1000
MAX_PULSE = 2.5/1000

# 足端平衡位置
X_CENTER = 0.0
Z_CENTER = -0.08

# 步态参数
STEP_A = 0.03   # 前后幅度
STEP_B = 0.02   # 抬腿高度
T_CYCLE = 1.0   # 每步周期 (秒)

# ==================================================

def inverse_kinematics(x, z, L1, L2):
    """二维两连杆逆运动学：由(x, z)求(θ1, θ2)，返回弧度"""
    d = math.sqrt(x**2 + z**2)
    if d > (L1 + L2):
        d = L1 + L2  # 限幅，防止超出可达
    cos_t2 = (x**2 + z**2 - L1**2 - L2**2) / (2 * L1 * L2)
    cos_t2 = max(-1, min(1, cos_t2))
    t2 = math.acos(cos_t2)
    t1 = math.atan2(x, -z) - math.atan2(L2 * math.sin(t2), L1 + L2 * math.cos(t2))
    return t1, t2

class Quadruped2DOF:
    def __init__(self, pins):
        self.servos = {}
        for name, pin in pins.items():
            self.servos[name] = AngularServo(pin,
                                             min_angle=MIN_ANGLE,
                                             max_angle=MAX_ANGLE,
                                             min_pulse_width=MIN_PULSE,
                                             max_pulse_width=MAX_PULSE)
        self.pose_stand()

    def set_leg_angles(self, leg, theta1, theta2):
        """设置单腿角度（弧度 -> 度）"""
        hip_servo = self.servos[f"{leg}_hip"]
        knee_servo = self.servos[f"{leg}_knee"]
        hip_servo.angle = math.degrees(theta1)
        knee_servo.angle = math.degrees(theta2)

    def set_leg_position(self, leg, x, z):
        """通过逆运动学设置足端位置"""
        theta1, theta2 = inverse_kinematics(x, z, L1, L2)
        self.set_leg_angles(leg, theta1, theta2)

    def pose_stand(self):
        """站立姿态"""
        for leg in ("LF", "RF", "LH", "RH"):
            self.set_leg_position(leg, X_CENTER, Z_CENTER)

    def walk_trot(self, steps=2):
        """执行若干步对角步态"""
        dt = 0.05
        t = 0
        while steps > 0:
            # 四条腿步态相位（对角相反）
            phase = {
                "LF": 0,
                "RH": 0,
                "RF": math.pi,
                "LH": math.pi
            }
            for leg, phi in phase.items():
                # 每个腿的轨迹
                x = X_CENTER + STEP_A * math.sin(2*math.pi*t/T_CYCLE + phi)
                z = Z_CENTER + STEP_B * max(0, math.cos(2*math.pi*t/T_CYCLE + phi))
                self.set_leg_position(leg, x, z)

            t += dt
            if t > T_CYCLE:
                t = 0
                steps -= 1
            sleep(dt)

    def close(self):
        for s in self.servos.values():
            try:
                s.close()
            except:
                pass

# ==================================================
if __name__ == "__main__":
    bot = Quadruped2DOF(PINS)
    try:
        print("🐾 初始化完成，开始走动！")
        bot.walk_trot(steps=4)
        print("✅ 完成，回到站立姿态")
        bot.pose_stand()
    except KeyboardInterrupt:
        pass
    finally:
        bot.close()
        print("GPIO 已释放。")

🧾 五、代码讲解（运动学 & 步态）

段落 含义
inverse_kinematics(x,z) 由足端目标位置求两舵机角度，采用标准 2-Link 逆解公式
set_leg_position() 将足端坐标转为舵机角度并发送
walk_trot() 以对角步形式生成足端轨迹（正弦 + 余弦控制）
phase 用 π 的相位差让对角腿交替动作
z 轨迹中 max(0, cos(...)) 确保"抬脚"时 z 增大，"支撑"时不穿地

🧮 六、简单数值例子（逆运动学验证）

若：

  • L 1 = L 2 = 0.05   m L_1 = L_2 = 0.05\,m L1=L2=0.05m
  • 足端目标 x = 0.03 , z = − 0.08 x = 0.03, z = -0.08 x=0.03,z=−0.08

则：

cos ⁡ ( θ 2 ) = 0.0 3 2 + 0.0 8 2 − 0.0 5 2 − 0.0 5 2 2 × 0.05 × 0.05 = 0.28 ⇒ θ 2 ≈ 73.7 ° \cos(\theta_2) = \frac{0.03^2 + 0.08^2 - 0.05^2 - 0.05^2}{2×0.05×0.05} = 0.28 \Rightarrow \theta_2 ≈ 73.7° cos(θ2)=2×0.05×0.050.032+0.082−0.052−0.052=0.28⇒θ2≈73.7°

θ 1 = arctan ⁡ 2 ( 0.03 , 0.08 ) − arctan ⁡ 2 ( 0.05 sin ⁡ 73.7 ° , 0.05 + 0.05 cos ⁡ 73.7 ° ) ≈ 18.4 ° − 24.7 ° = − 6.3 ° \theta_1 = \arctan2(0.03, 0.08) - \arctan2(0.05\sin73.7°, 0.05+0.05\cos73.7°) ≈ 18.4° - 24.7° = -6.3° θ1=arctan2(0.03,0.08)−arctan2(0.05sin73.7°,0.05+0.05cos73.7°)≈18.4°−24.7°=−6.3°

也就是说，髋关节稍向后倾 (-6°)，膝关节弯曲 74°，脚端正好在目标位置。

⚡ 七、调试与建议

  1. 先测试单腿 ：

    用 set_leg_position("LF", 0.0, -0.07) 单步测试每条腿运动范围是否正确。

  2. 调整坐标方向 ：

    某些舵机安装方向可能相反，如抬脚反而向下，可反转角度符号：

    python 复制代码 
    hip_servo.angle = -math.degrees(theta1)

  3. 供电建议 ：

    八个舵机需稳定 5V ≥ 3A 电源；Raspberry Pi GPIO 仅输出信号，不可直接供电。

  4. 扩展步态 ：

    可进一步加入 相位差偏移 或 中心模式发生器（CPG） 生成更平滑的步态。

🧭 八、总结（与4舵机版对比）

项目 4舵机版 8舵机版
自由度/腿 1 2
是否能抬腿 ❌ 否 ✅ 是
是否真实步态 模拟拖动 可实现步行
运动学复杂度 一元（单角度） 二连杆逆运动学
机械复杂度 低 中
步态类型 摆腿推进 抬腿步行

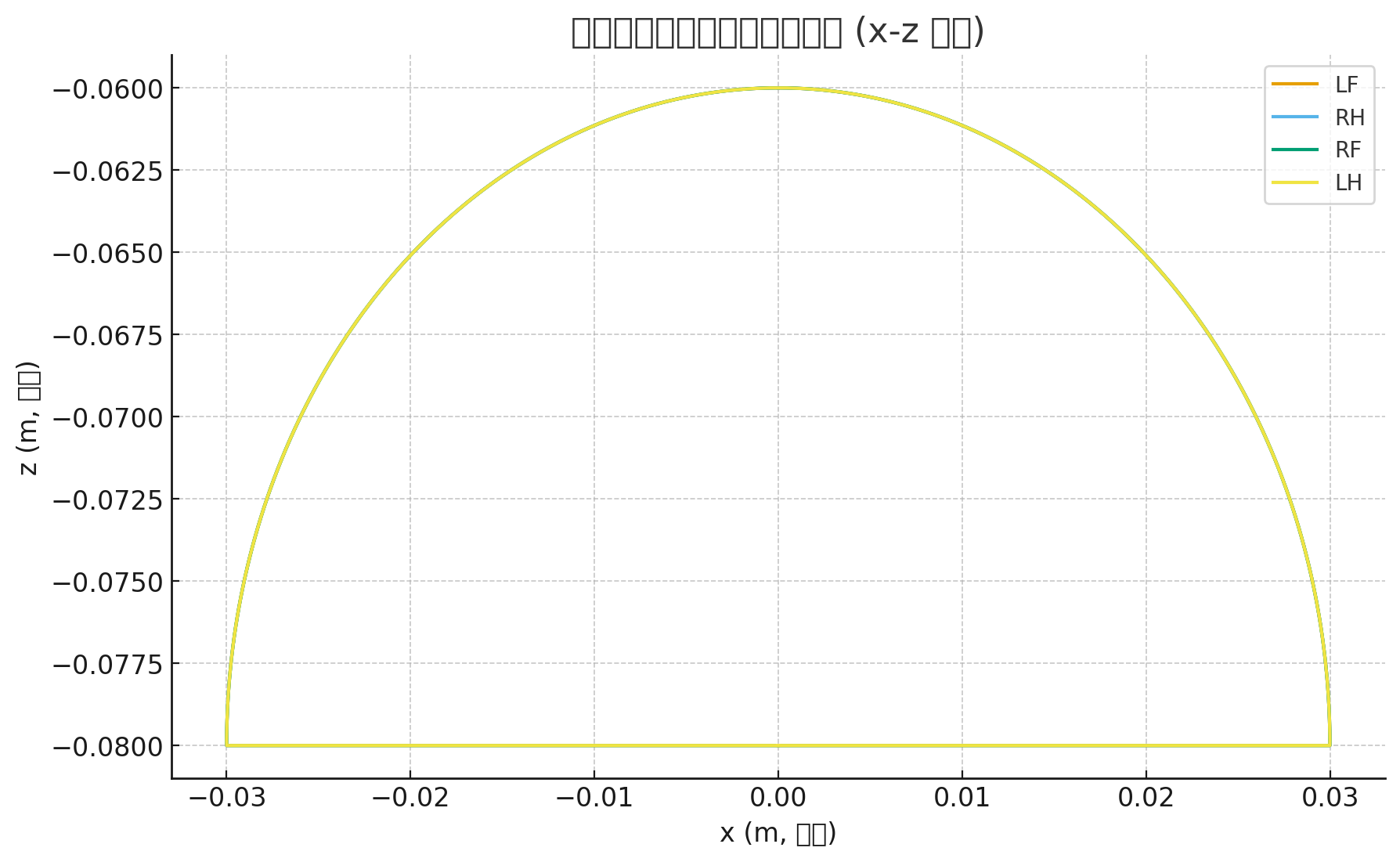
上面的图展示了四足机器人每条腿在一个完整步态周期内的 足端轨迹 (x--z 平面)：

  • 横轴 (x) 表示前后方向（步幅范围约 ±0.03 m）。
  • 纵轴 (z) 表示上下方向（抬脚高度约 0.02 m）。
  • 蓝/橙 vs 绿/红 两组腿分别对应对角步（LF+RH 与 RF+LH 相反相位）。

可以看到：

  • 每条腿的轨迹形成一个"半椭圆形循环"；
  • 前进相（腿抬起并向前摆动）时，z 值上升；
  • 支撑相（腿接地推地）时，z 值维持在下方并向后移动；
  • 对角腿的轨迹完全相反，保证了机器人在步行时始终有两个支撑点维持平衡。

CPG（中央模式发生器）控制框架 ，用于那台 8 舵机 / 2 DOF 每腿 的四足机器人。

  1. CPG 原理与数学（简明、能直接实现）
  2. 可运行的 Python 代码（含模拟模式与真实硬件模式）------把 CPG 输出映射到每条腿的足端轨迹，再用逆运动学转成舵机角度。
  3. 调参与调试建议（如何让机器人走得稳、如何改步态）

1) CPG 简介与数学（直接可用）

我们用 相位振荡器（phase oscillator）耦合网络 实现 CPG ------ 简单、稳定、且能通过相位差产生常见步态（walk / trot / pace / bound）。

每个腿用一个振荡器 ϕ i ( t ) \phi_i(t) ϕi(t)（相位）和幅值控制（步幅/抬脚高度可做成常数或受振幅振荡器影响）。振荡器的更新（离散时间）：

ϕ ˙ i = ω i + ∑ j K i j sin ⁡ ( ϕ j − ϕ i − Δ i j ) \dot\phi_i = \omega_i + \sum_{j} K_{ij}\sin(\phi_j - \phi_i - \Delta_{ij}) ϕ˙i=ωi+j∑Kijsin(ϕj−ϕi−Δij)

离散步进实现为：

text 复制代码 
phi_i += (omega_i + sum_j K_ij * sin(phi_j - phi_i - Delta_ij)) * dt
phi_i = phi_i % (2*pi)

其中：

  • ω i = 2 π f \omega_i = 2\pi f ωi=2πf（步频）
  • K i j K_{ij} Kij 耦合强度（常取同一值 K）
  • Δ i j \Delta_{ij} Δij 目标相位差（用于指定步态，例如对角步 trot：LF and RH 同相，RF/LH 同相，相位相差 π）

把相位映射到足端轨迹（x,z）：

  • x i ( t ) = x c + A sin ⁡ ( ϕ i ) x_i(t) = x_c + A \sin(\phi_i) xi(t)=xc+Asin(ϕi) （前后）
  • z i ( t ) = z c + B max ⁡ ( 0 , cos ⁡ ( ϕ i ) ) z_i(t) = z_c + B \max(0, \cos(\phi_i)) zi(t)=zc+Bmax(0,cos(ϕi)) （抬脚只在某相位段发生）

然后对 (x,z) 做逆运动学求出髋/膝角度，发送到舵机。

2) 完整 Python 代码（含模拟和硬件两种模式）

⚠️ 运行注意：真实硬件模式会使用 gpiozero.AngularServo 控制舵机，请先确认引脚、脉宽、外接电源与共地。

模拟模式只画图与动画，不触及 GPIO（安全便于调参）。

把下面代码保存为 cpg_quadruped.py，按需修改 PINS 与几何参数，然后运行。

python 复制代码 
"""
cpg_quadruped.py
CPG 控制 8 舵机四足机器人（2DOF/腿）
Mode: simulation (matplotlib) or hardware (gpiozero)
"""

import math
import time
import numpy as np

# === 如果要在真实机器人上跑，把 USE_HARDWARE=True ===
USE_HARDWARE = False

if USE_HARDWARE:
    from gpiozero import AngularServo

# ------------------ 参数 ------------------
# BCM 引脚示例（按你实际接线调整）
PINS = {
    "LF_hip": 17,  "LF_knee": 18,
    "RF_hip": 27,  "RF_knee": 22,
    "LH_hip": 23,  "LH_knee": 24,
    "RH_hip": 25,  "RH_knee": 5,
}

# 机械几何（米）
L1 = 0.05   # 大腿
L2 = 0.05   # 小腿
X_CENTER = 0.0
Z_CENTER = -0.08

# CPG 参数（可以调）
STEP_A = 0.03    # 水平步幅（m）
STEP_B = 0.02    # 抬脚高度（m）
FREQ = 1.0       # 步频 Hz
OMEGA = 2 * math.pi * FREQ
K_COUPLING = 8.0 # 耦合强度（较大值使相位锁定更快）
DT = 0.02        # 控制循环时间步长（秒）

# 舵机角度 / 脉宽（硬件模式用）
MIN_ANGLE = -90
MAX_ANGLE = 90
MIN_PULSE = 0.5/1000
MAX_PULSE = 2.5/1000

# 腿列表顺序
LEGS = ["LF", "RF", "LH", "RH"]

# 目标相位差矩阵（根据步态选择）
# 对角步 trot: LF & RH 相位相同, RF & LH 相差 pi
PHASE_OFFSETS = {
    "LF": 0.0,
    "RH": 0.0,
    "RF": math.pi,
    "LH": math.pi
}

# -------------------------------------------

def inverse_kinematics(x, z, L1=L1, L2=L2):
    """2-link IK: 返回 (theta1_rad, theta2_rad)"""
    d = math.hypot(x, z)
    # 限幅
    if d > (L1 + L2):
        scale = (L1 + L2) / d
        x *= scale
        z *= scale
        d = L1 + L2
    cos_t2 = (x*x + z*z - L1*L1 - L2*L2) / (2 * L1 * L2)
    cos_t2 = max(-1.0, min(1.0, cos_t2))
    t2 = math.acos(cos_t2)
    t1 = math.atan2(x, -z) - math.atan2(L2 * math.sin(t2), L1 + L2 * math.cos(t2))
    return t1, t2

class CPGNetwork:
    def __init__(self, legs=LEGS, omega=OMEGA, K=K_COUPLING, phase_offsets=PHASE_OFFSETS, dt=DT):
        self.legs = legs
        self.n = len(legs)
        self.dt = dt
        self.omega = omega
        self.K = K
        # 相位向量初始化
        self.phi = {leg: phase_offsets.get(leg, 0.0) for leg in legs}
        # 理想相位差 Delta_ij = phi_j* - phi_i* (we'll use pairwise desired differences from phase_offsets)
        self.desired = {}
        for i in legs:
            for j in legs:
                self.desired[(i,j)] = (phase_offsets[j] - phase_offsets[i])
    
    def step(self):
        # 相位更新（显式 Euler）
        dphi = {}
        for i in self.legs:
            coupling_sum = 0.0
            for j in self.legs:
                if i == j: continue
                Delta_ij = self.desired[(i,j)]
                coupling_sum += math.sin(self.phi[j] - self.phi[i] - Delta_ij)
            dphi[i] = (self.omega + self.K * coupling_sum) * self.dt
        for i in self.legs:
            self.phi[i] = (self.phi[i] + dphi[i]) % (2*math.pi)
        return self.phi.copy()

class QuadrupedCPG:
    def __init__(self, use_hardware=False):
        self.use_hw = use_hardware
        if self.use_hw:
            # 创建舵机对象
            self.servos = {}
            for leg in LEGS:
                hip_name = f"{leg}_hip"
                knee_name = f"{leg}_knee"
                self.servos[hip_name] = AngularServo(PINS[hip_name], min_angle=MIN_ANGLE, max_angle=MAX_ANGLE,
                                                    min_pulse_width=MIN_PULSE, max_pulse_width=MAX_PULSE)
                self.servos[knee_name] = AngularServo(PINS[knee_name], min_angle=MIN_ANGLE, max_angle=MAX_ANGLE,
                                                     min_pulse_width=MIN_PULSE, max_pulse_width=MAX_PULSE)
        else:
            self.servos = None
        self.cpg = CPGNetwork()
    
    def phase_to_foot(self, phi, leg):
        """把单腿相位映射为足端 (x,z)"""
        x = X_CENTER + STEP_A * math.sin(phi)
        # 抬脚仅在 cos(phi) > 0 时发生（简单的切割）
        z = Z_CENTER + STEP_B * max(0.0, math.cos(phi))
        return x, z
    
    def send_leg_angles(self, leg, theta1_rad, theta2_rad):
        if self.use_hw:
            hip_servo = self.servos[f"{leg}_hip"]
            knee_servo = self.servos[f"{leg}_knee"]
            # 角度到度，注意方向可能需要根据舵机安装翻转符号
            hip_servo.angle = math.degrees(theta1_rad)
            knee_servo.angle = math.degrees(theta2_rad)
        else:
            # 模拟模式：返回值给上层用于绘图或日志
            return math.degrees(theta1_rad), math.degrees(theta2_rad)
    
    def step_and_apply(self):
        phi_dict = self.cpg.step()
        angles_out = {}
        for leg, phi in phi_dict.items():
            x, z = self.phase_to_foot(phi, leg)
            t1, t2 = inverse_kinematics(x, z)
            res = self.send_leg_angles(leg, t1, t2)
            angles_out[leg] = {
                "phi": phi,
                "foot": (x, z),
                "angles_deg": res
            }
        return angles_out

    def close(self):
        if self.use_hw and self.servos:
            for s in self.servos.values():
                try:
                    s.close()
                except:
                    pass

# --------------- 模拟运行 / 演示 ---------------
def simulate(duration=4.0):
    import matplotlib.pyplot as plt
    from matplotlib.animation import FuncAnimation

    robot = QuadrupedCPG(use_hardware=False)
    t = 0.0
    steps = int(duration / DT)
    # 保存数据以可视化
    data = {leg: {"x": [], "z": [], "phi": []} for leg in LEGS}
    for _ in range(steps):
        out = robot.step_and_apply()
        for leg in LEGS:
            x,z = out[leg]["foot"]
            data[leg]["x"].append(x)
            data[leg]["z"].append(z)
            data[leg]["phi"].append(out[leg]["phi"])
        t += DT

    # 绘图：四条腿 x-z 轨迹（每条腿一条曲线）
    fig, ax = plt.subplots()
    for leg in LEGS:
        ax.plot(data[leg]["x"], data[leg]["z"], label=leg)
    ax.set_xlabel("x (m)")
    ax.set_ylabel("z (m)")
    ax.set_title("CPG 生成的足端轨迹 (x-z) over time")
    ax.legend()
    ax.grid(True)
    plt.show()

    # 可选：相位随时间变化图
    fig2, ax2 = plt.subplots()
    times = np.linspace(0, duration, len(data[LEGS[0]]["phi"]))
    for leg in LEGS:
        ax2.plot(times, np.unwrap(data[leg]["phi"]), label=leg)
    ax2.set_xlabel("time (s)")
    ax2.set_ylabel("phase (rad)")
    ax2.set_title("CPG 相位随时间演化")
    ax2.legend()
    ax2.grid(True)
    plt.show()

# --------------- 硬件运行主循环 ---------------
def run_on_hardware(runtime=10.0):
    robot = QuadrupedCPG(use_hardware=True)
    start = time.time()
    try:
        while time.time() - start < runtime:
            out = robot.step_and_apply()
            # 这里可以加日志或安全检查
            time.sleep(DT)
    except KeyboardInterrupt:
        print("用户中断")
    finally:
        robot.close()

# --------------- 入口 ---------------
if __name__ == "__main__":
    if USE_HARDWARE:
        print("Running on hardware mode")
        run_on_hardware(runtime=20.0)
    else:
        print("Simulation mode (no GPIO).")
        simulate(duration=6.0)

代码说明亮点：

  • CPGNetwork：实现相位耦合更新（简洁的 Kuramoto-like 形式但带目标相位差）。
  • phase_to_foot()：把相位转换为足端轨迹（x,z）。可以替换为更复杂的轨迹（如椭圆、Bezier）。
  • QuadrupedCPG.step_and_apply()：每个控制循环产生相位、计算 IK、并（在硬件模式）发送角度或（在模拟模式）返回用于绘图。
  • simulate()：在不接触硬件时可快速画出轨迹与相位曲线，便于调参。

3) 如何通过 CPG 参数调节不同步态与运动特性

  1. 步态类型（相位偏移）

    • 对角步（trot）：LF=0, RH=0, RF=π, LH=π （代码中已设置）
    • 行走/walk（四步顺序）：设相位为 LF=0, RF=π/2, RH=π, LH=3π/2（每条腿相差 90°）
    • 同步 bound：LF=0, RF=0, LH=π, RH=π
    • 只要修改 PHASE_OFFSETS 即可切换步态。

  2. 步频 FREQ（ω）

    • 提高 FREQ 会加快步频；但舵机和机械动力学必须能跟上。小步频开始（0.5~1Hz），逐步增加。

  3. 耦合强度 K

    • 较高 K 会使相位锁定更快（尤其从随机初相过渡到稳定步态）。
    • 太高可能导致数值刚性（需要缩小 dt）。

  4. 步幅 STEP_A / 抬脚 STEP_B

    • 增大 STEP_A 增速度但可能超出可达空间或导致打滑。STEP_B 影响抬脚高度（太大可能舵机受力）。
    • 对 2DOF 结构，保证 (x,z) 始终在可达工作空间内： x 2 + z 2 ≤ L 1 + L 2 \sqrt{x^2+z^2} \le L1+L2 x2+z2 ≤L1+L2。

  5. 轨迹形状

    • 目前用 sin/cos + 半波整流（max(0,cos)）实现抬脚；要更自然可用参数化曲线（椭圆、Bezier），或用幅值振荡器把抬脚和支撑段连续平滑分开。

  6. 安全措施

    • 在硬件模式下，每次给舵机发送命令前做角度限位检查；并在启动阶段用低幅度慢速收敛到目标相位（warm-up）以避免突然冲击电流。

4) 调试步骤（推荐顺序）

  1. 模拟阶段（强烈推荐）

    • 把 USE_HARDWARE=False，运行 python cpg_quadruped.py，观察 x-z 轨迹与相位随时间变化，调整 STEP_A/STEP_B/FREQ/K 直到看起来合理。

  2. 单腿测试

    • 改 PHASE_OFFSETS 只保留一条腿非零相位，使用 QuadrupedCPG 的 phase_to_foot + inverse_kinematics 单独让某腿运行，观察舵机响应。

  3. 双腿/对角测试

    • 先只接两条对角腿（LF + RH）上电做 trot 测试，检查是否有足够摩擦推地、不抖动。

  4. 整机低幅度测试

    • 在硬件运行前把 STEP_A 和 STEP_B 缩小到 50% 或更低，慢速 warm-up（低 FREQ），观察电流与舵机温度。

  5. 逐步放大

    • 逐步增加步幅和频率，直到达到满意的速度或出现问题（打滑/舵机扭矩不足/失步），再回退并找原因。

8舵机步行机器人基础运动学系统 ，接下来加上"原地转向 / 后退 / 侧移"是非常自然的一步。

这一步的核心思想是：

💡 通过调节四条腿的步态相位和足端轨迹中心方向，控制整体运动矢量。

🧠 一、运动学思想：通过足端轨迹叠加生成机体运动

四足机器人有三个主要机体自由度：

模式 控制变量 步态调整原理
前进 / 后退 vx (前向速度) 改变足端轨迹的前后相位
侧移 vy (横向速度) 左右腿的轨迹中心对称偏移
原地转向 ω (角速度) 对角腿间的相位差加上旋转补偿

⚙️ 二、核心步态生成器 (Gait Generator)

让我们定义每条腿在局部坐标系下的足端轨迹：

x i ( t ) = x c + A x sin ⁡ ( ω t + ϕ i ) x_i(t) = x_c + A_x \sin(\omega t + \phi_i) xi(t)=xc+Axsin(ωt+ϕi)

y i ( t ) = y c + A y cos ⁡ ( ω t + ϕ i ) y_i(t) = y_c + A_y \cos(\omega t + \phi_i) yi(t)=yc+Aycos(ωt+ϕi)

z i ( t ) = z c + B ⋅ max ⁡ ( 0 , cos ⁡ ( ω t + ϕ i ) ) z_i(t) = z_c + B \cdot \max(0, \cos(\omega t + \phi_i)) zi(t)=zc+B⋅max(0,cos(ωt+ϕi))

其中：

  • A x , A y A_x, A_y Ax,Ay 控制步幅和侧移幅；
  • ϕ i \phi_i ϕi 控制腿的步态相位；
  • ω = 2 π / T ω = 2π/T ω=2π/T 控制步频；
  • max(0, cos()) 确保抬脚时才上升；
  • 通过相位组合 (LF,RH) 同步、(RF,LH) 相反，实现对角步 或原地转向步。

🧩 三、不同动作的相位/方向配置

动作 参数 特征
前进 vx > 0, vy = 0, ω = 0 对角步
后退 vx < 0 相位不变但轨迹反向
侧移 vy ≠ 0 左右腿轨迹 y 偏移相反
原地转向 ω ≠ 0 四腿以不同相位绕中心旋转，(LF, RH) 与 (RF, LH) 反向摆动

🧮 四、完整 Python 控制框架

下面这段代码在之前的 8 舵机机器人基础上扩展，加入了通用步态控制，可设定方向与角速度。

✅ 理论兼容 Raspberry Pi + gpiozero 实机控制

💡 若在电脑上仅模拟，可只运行轨迹部分看运动规律

python 复制代码 
import math, time
from gpiozero import AngularServo

# ========== 参数配置 ==========
PINS = {
    "LF_hip": 17, "LF_knee": 18,
    "RF_hip": 27, "RF_knee": 22,
    "LH_hip": 23, "LH_knee": 24,
    "RH_hip": 25, "RH_knee": 5,
}

L1, L2 = 0.05, 0.05
X_CENTER, Z_CENTER = 0.0, -0.08
MIN_PULSE, MAX_PULSE = 0.5/1000, 2.5/1000
MIN_ANGLE, MAX_ANGLE = -90, 90
STEP_A, STEP_B = 0.03, 0.02
T_CYCLE = 1.0

def ik(x, z):
    """逆运动学"""
    d = math.sqrt(x**2 + z**2)
    d = min(max(d, 1e-6), L1 + L2)
    cos_t2 = (x**2 + z**2 - L1**2 - L2**2) / (2 * L1 * L2)
    cos_t2 = max(-1, min(1, cos_t2))
    t2 = math.acos(cos_t2)
    t1 = math.atan2(x, -z) - math.atan2(L2 * math.sin(t2), L1 + L2 * math.cos(t2))
    return t1, t2

class Quadruped:
    def __init__(self):
        self.servos = {
            k: AngularServo(v, min_angle=MIN_ANGLE, max_angle=MAX_ANGLE,
                            min_pulse_width=MIN_PULSE, max_pulse_width=MAX_PULSE)
            for k, v in PINS.items()
        }
        self.pose_stand()

    def set_leg(self, leg, x, z):
        t1, t2 = ik(x, z)
        self.servos[f"{leg}_hip"].angle = math.degrees(t1)
        self.servos[f"{leg}_knee"].angle = math.degrees(t2)

    def pose_stand(self):
        for leg in ("LF","RF","LH","RH"):
            self.set_leg(leg, X_CENTER, Z_CENTER)

    def gait(self, vx=0, vy=0, yaw_rate=0, steps=2):
        """vx,vy: 线速度 (m/s); yaw_rate: 角速度(rad/s)"""
        dt = 0.05
        t = 0
        while steps > 0:
            ω = 2 * math.pi / T_CYCLE
            for leg, phi in {"LF":0, "RH":0, "RF":math.pi, "LH":math.pi}.items():
                # 旋转方向偏移
                yaw_dir = 1 if leg in ("LF","LH") else -1
                # 轨迹中心 (控制侧移 + 转向)
                x_c = X_CENTER + vx * 0.3 + yaw_dir * yaw_rate * 0.02
                y_c = vy * yaw_dir * 0.02
                # 足端轨迹
                x = x_c + STEP_A * math.sin(ω*t + phi)
                z = Z_CENTER + STEP_B * max(0, math.cos(ω*t + phi))
                self.set_leg(leg, x, z)

            t += dt
            if t > T_CYCLE:
                t = 0
                steps -= 1
            time.sleep(dt)

    def close(self):
        for s in self.servos.values():
            try: s.close()
            except: pass

if __name__ == "__main__":
    bot = Quadruped()
    try:
        print("前进中...")
        bot.gait(vx=0.05, vy=0, yaw_rate=0, steps=2)

        print("后退中...")
        bot.gait(vx=-0.05, vy=0, yaw_rate=0, steps=2)

        print("右移中...")
        bot.gait(vx=0, vy=0.05, yaw_rate=0, steps=2)

        print("左转中...")
        bot.gait(vx=0, vy=0, yaw_rate=0.5, steps=2)

        print("右转中...")
        bot.gait(vx=0, vy=0, yaw_rate=-0.5, steps=2)

    except KeyboardInterrupt:
        pass
    finally:
        bot.close()
        print("GPIO 已释放。")

📘 五、运动学解释（以原地转向为例）

当设置 yaw_rate ≠ 0 时：

  • 左侧两条腿（LF, LH）的步态相位和足端中心向一个方向偏移；
  • 右侧两条腿（RF, RH）相反；
  • 结果是足端运动围绕机体中心形成一个"旋转矢量场"，产生角速度。

这是在四足机器人中模拟"Yaw 旋转"的常见运动学策略。

✅ 实际中，可以把 yaw_rate 映射到每条腿在平面的旋转半径 r_i：

x i ′ = x c + r i sin ⁡ ( ω t + ϕ i ) , y i ′ = y c + r i cos ⁡ ( ω t + ϕ i ) x_i' = x_c + r_i \sin(\omega t + \phi_i), \quad y_i' = y_c + r_i \cos(\omega t + \phi_i) xi′=xc+risin(ωt+ϕi),yi′=yc+ricos(ωt+ϕi)

从而得到更加平滑的转向步态。

🧭 六、动作总结

动作类型 参数设置示例 描述
前进 gait(vx=0.05) 对角步推进
后退 gait(vx=-0.05) 相同相位反向运动
侧移 gait(vy=0.05) 左右对称横移
左转 gait(yaw_rate=0.5) 原地逆时针转向
右转 gait(yaw_rate=-0.5) 原地顺时针转向
相关推荐
武子康3 小时前
AI-调查研究-107-具身智能 强化学习与机器人训练数据格式解析：从状态-动作对到多模态轨迹标准
人工智能·深度学习·机器学习·ai·系统架构·机器人·具身智能
沫儿笙3 小时前
KUKA库卡焊接机器人二氧化碳节气
人工智能·机器人
insight^tkk4 小时前
【Docker】记录一次使用docker部署dify网段冲突的问题
运维·人工智能·docker·ai·容器
攻城狮7号4 小时前
AI+大数据时代：如何从架构到生态重构时序数据库的价值？
大数据·人工智能·时序数据库·apache iotdb·sql大模型
智能化咨询4 小时前
AI+大数据时代：时序数据库的生态重构与价值跃迁——从技术整合到行业落地
人工智能
paopaokaka_luck4 小时前
基于SpringBoot+Vue的社区诊所管理系统（AI问答、webSocket实时聊天、Echarts图形化分析）
vue.js·人工智能·spring boot·后端·websocket
工藤学编程4 小时前
零基础学AI大模型之RAG系统链路解析与Document Loaders多案例实战
人工智能
大千AI助手4 小时前
加权分位数直方图：提升机器学习效能的关键技术
人工智能·机器学习·xgboost·直方图·加权直方图·特征分裂
星期天要睡觉4 小时前
深度学习——基于ResNet18迁移学习的图像分类模型
人工智能·python·分类·迁移学习
热门推荐
01BongoCat - 跨平台键盘猫动画工具02GitHub 镜像站点03UV安装并设置国内源04两千字总结：Codex 国内如何安装和使用的教程，以及如何设置中文回答05Linux下V2Ray安装配置指南06KGG转MP3工具|非KGM文件|解密音频07GitLab 零基础入门指南：从安装到项目管理全流程08荣耀手机2025年10月发布的新品Magic8比起Magic7，在硬件、性能、价格等上有什么区别，有什么优势09windows找不到gpedit.msc（本地组策略编辑器）10在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）