BFS 与 DFS——力扣102.二叉树的层序遍历

力扣102.二叉树的层序遍历

LeetCode 102. 二叉树的层序遍历：从 BFS 到 DFS 的两种写法详解

一、题目描述

给定一个二叉树的根节点 root，返回其节点值的层序遍历结果。

层序遍历是指逐层、从左到右 地访问所有节点。

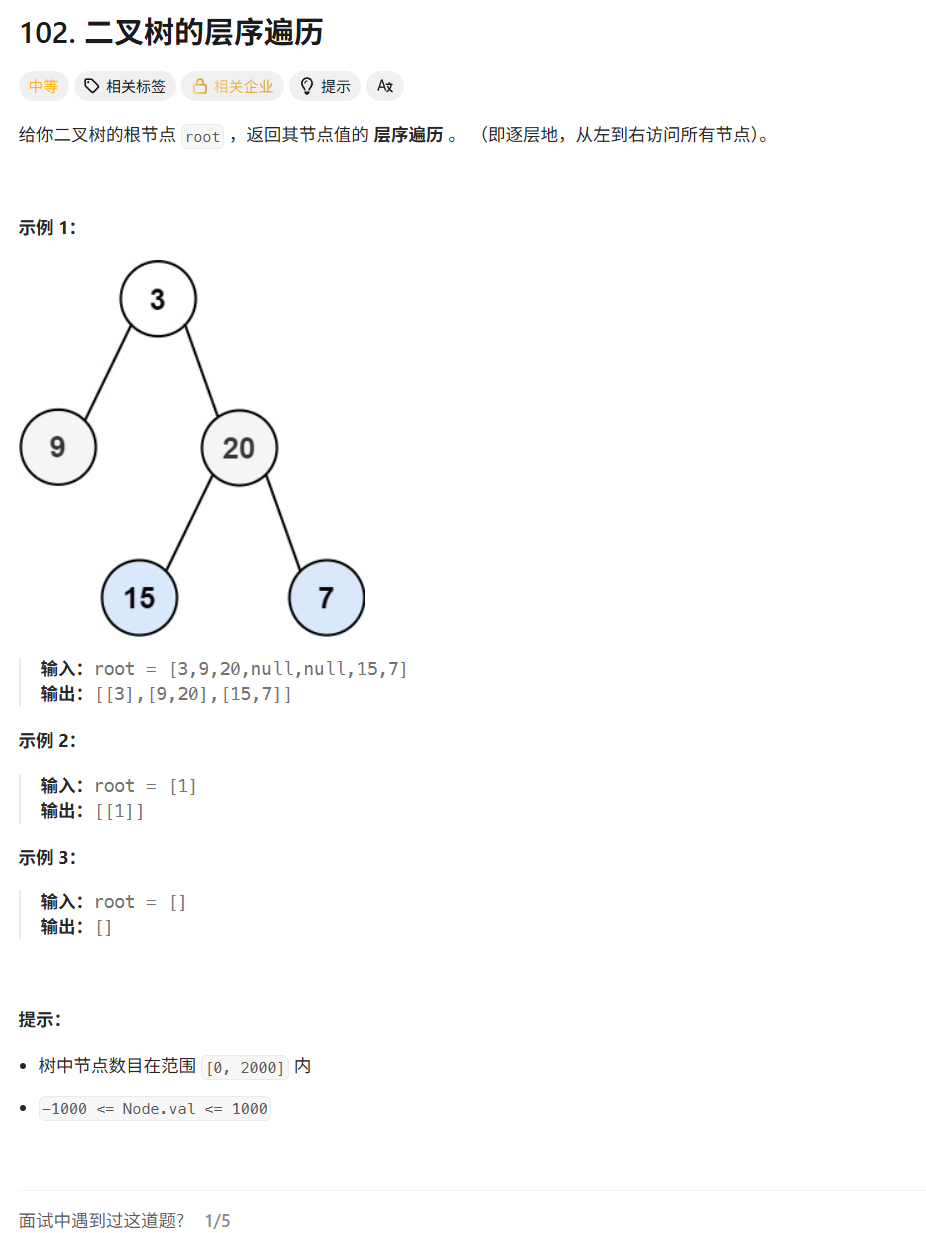
示例 1：

复制代码

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

复制代码

输入：root = [1]
输出：[[1]]

示例 3：

复制代码

输入：root = []
输出：[]

提示：

树中节点数量范围：[0, 2000]
节点值范围：[-1000, 1000]

二、题意分析

层序遍历是最经典的 广度优先搜索（BFS） 场景之一。

核心思想是利用队列（Queue）逐层存储节点：

每次取出队列中当前层的所有节点；
访问它们的值；
将它们的左右孩子加入队列；
重复直到队列为空。

此外，也可以用 深度优先搜索（DFS） 结合层数信息实现相同的效果。

三、解法一：BFS（队列实现）

1. 思路讲解

创建一个队列 Queue<TreeNode>；
初始时将根节点入队；
当队列不为空时：
- 记录当前层的节点数量；
- 遍历该层的所有节点，取出节点值；
- 将左右子节点加入队列；
- 将本层结果加入最终结果列表。

2. 代码实现（推荐写法）

java 复制代码

import java.util.*;

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> result = new ArrayList<>();
        if (root == null) return result;

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while (!queue.isEmpty()) {
            int size = queue.size();
            List<Integer> level = new ArrayList<>();

            for (int i = 0; i < size; i++) {
                TreeNode node = queue.poll();
                level.add(node.val);

                if (node.left != null) queue.offer(node.left);
                if (node.right != null) queue.offer(node.right);
            }

            result.add(level);
        }

        return result;
    }
}

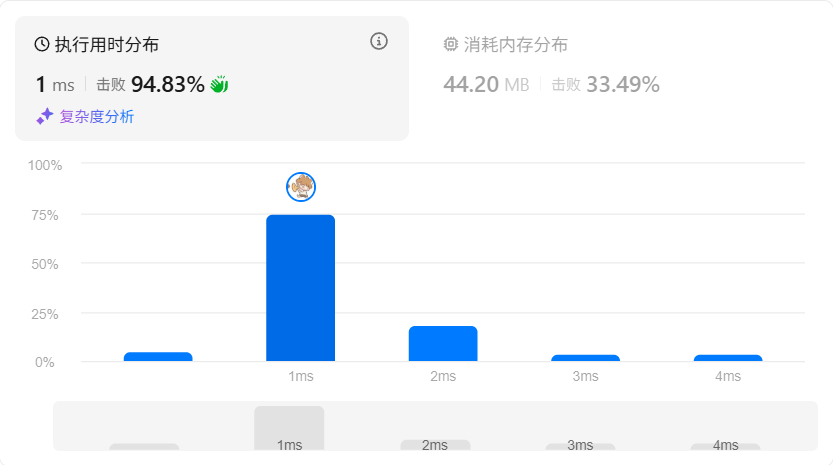
3. 复杂度分析

项目	复杂度	说明
时间复杂度	O(n)	每个节点访问一次
空间复杂度	O(n)	队列最多存储一层节点

四、解法二：DFS（递归实现）

1. 思路讲解

使用 DFS 递归时，传入当前节点与层数 level：

若 result.size() == level，说明是新的一层，需要新建一个列表；
将当前节点的值添加到对应层的列表中；
递归访问左子树与右子树，层数加 1。

2. 代码实现

java 复制代码

import java.util.*;

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> result = new ArrayList<>();
        dfs(root, 0, result);
        return result;
    }

    private void dfs(TreeNode node, int level, List<List<Integer>> result) {
        if (node == null) return;

        if (result.size() == level) {
            result.add(new ArrayList<>());
        }

        result.get(level).add(node.val);

        dfs(node.left, level + 1, result);
        dfs(node.right, level + 1, result);
    }
}

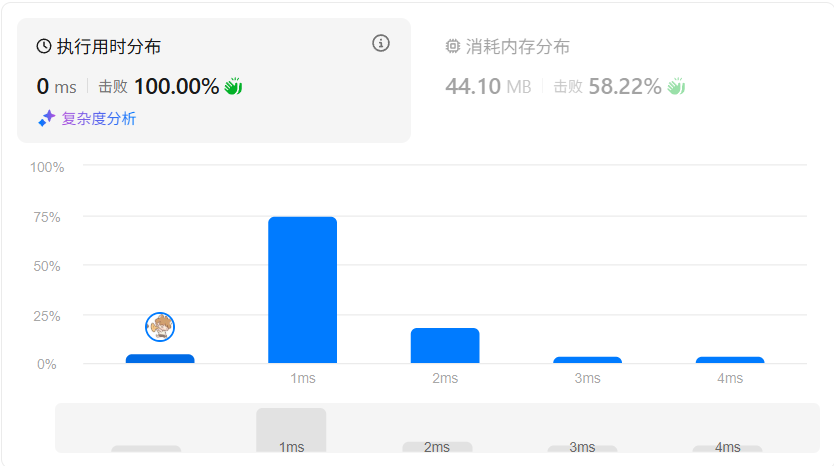
3. 复杂度分析

项目	复杂度	说明
时间复杂度	O(n)	每个节点遍历一次
空间复杂度	O(h)	递归栈高度为树的高度（最坏 O(n)）

五、方法对比总结

方法	思路核心	是否递归	时间复杂度	空间复杂度	适用场景
BFS	队列逐层扫描	否	O(n)	O(n)	常规、直观
DFS	递归分层收集	是	O(n)	O(h)	适合喜欢递归思维者

六、拓展思考

层序遍历变体：
- 自底向上的层序遍历（反转结果列表）；
- 每层节点平均值；
- 锯齿形层序遍历（Zigzag Level Order）。
面试延伸：
- 层序遍历在 BFS、图搜索、最短路径问题中均有广泛应用；
- 掌握 BFS 思路后，可以轻松应对拓扑排序、岛屿问题等题型。

七、总结

核心模板： 队列存当前层节点，遍历时入下一层；
可选写法： 递归 DFS，通过层数控制分层；
掌握层序遍历思想，是理解 BFS 核心的关键一步。